Path convergence of Markov chains on large graphs

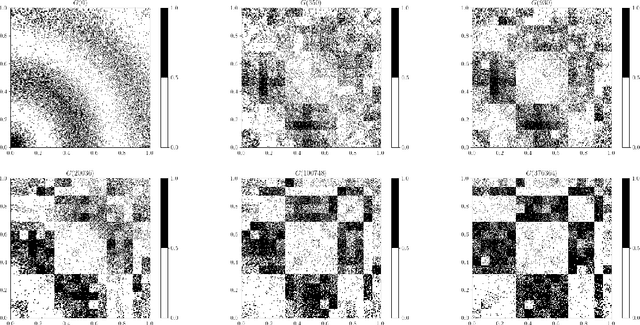
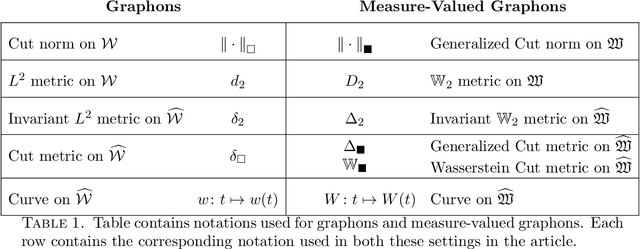
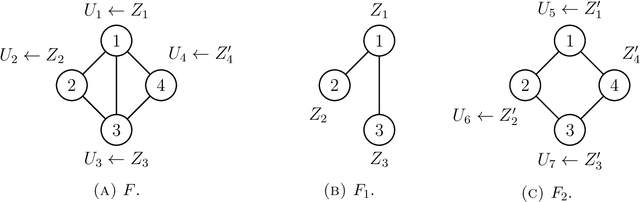
We consider two classes of natural stochastic processes on finite unlabeled graphs. These are Euclidean stochastic optimization algorithms on the adjacency matrix of weighted graphs and a modified version of the Metropolis MCMC algorithm on stochastic block models over unweighted graphs. In both cases we show that, as the size of the graph goes to infinity, the random trajectories of the stochastic processes converge to deterministic limits. These deterministic limits are curves on the space of measure-valued graphons. Measure-valued graphons, introduced by Lov\'{a}sz and Szegedy, are a refinement of the concept of graphons that can distinguish between two infinite exchangeable arrays that give rise to the same graphon limit. We introduce new metrics on this space which provide us with a natural notion of convergence for our limit theorems. This notion is equivalent to the convergence of infinite-exchangeable arrays. Under a suitable time-scaling, the Metropolis chain admits a diffusion limit as the number of vertices go to infinity. We then demonstrate that, in an appropriately formulated zero-noise limit, the stochastic process of adjacency matrices of this diffusion converge to a deterministic gradient flow curve on the space of graphons introduced in arXiv:2111.09459 [math.PR]. Under suitable assumptions, this allows us to estimate an exponential convergence rate for the Metropolis chain in a certain limiting regime. To the best of our knowledge, both the actual rate and the connection between a natural Metropolis chain commonly used in exponential random graph models and gradient flows on graphons are new in the literature.

Stochastic optimization on matrices and a graphon McKean-Vlasov limit

We consider stochastic gradient descents on the space of large symmetric matrices of suitable functions that are invariant under permuting the rows and columns using the same permutation. We establish deterministic limits of these random curves as the dimensions of the matrices go to infinity while the entries remain bounded. Under a ``small noise'' assumption the limit is shown to be the gradient flow of functions on graphons whose existence was established in arXiv:2111.09459. We also consider limits of stochastic gradient descents with added properly scaled reflected Brownian noise. The limiting curve of graphons is characterized by a family of stochastic differential equations with reflections and can be thought of as an extension of the classical McKean-Vlasov limit for interacting diffusions. The proofs introduce a family of infinite-dimensional exchangeable arrays of reflected diffusions and a novel notion of propagation of chaos for large matrices of interacting diffusions.

Gradient flows on graphons: existence, convergence, continuity equations

Wasserstein gradient flows on probability measures have found a host of applications in various optimization problems. They typically arise as the continuum limit of exchangeable particle systems evolving by some mean-field interaction involving a gradient-type potential. However, in many problems, such as in multi-layer neural networks, the so-called particles are edge weights on large graphs whose nodes are exchangeable. Such large graphs are known to converge to continuum limits called graphons as their size grow to infinity. We show that the Euclidean gradient flow of a suitable function of the edge-weights converges to a novel continuum limit given by a curve on the space of graphons that can be appropriately described as a gradient flow or, more technically, a curve of maximal slope. Several natural functions on graphons, such as homomorphism functions and the scalar entropy, are covered by our set-up, and the examples have been worked out in detail.

LLC: Accurate, Multi-purpose Learnt Low-dimensional Binary Codes

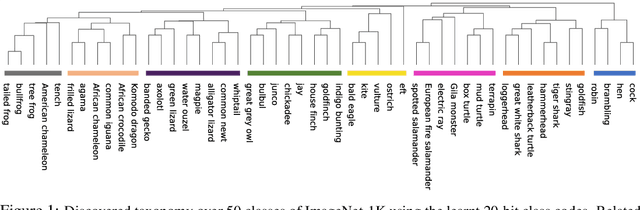
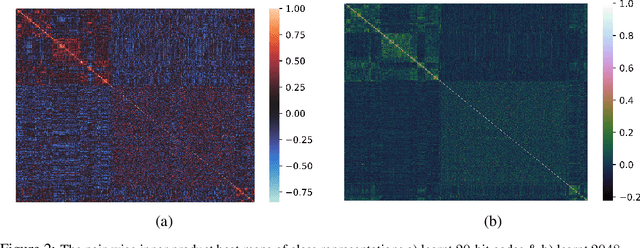
Learning binary representations of instances and classes is a classical problem with several high potential applications. In modern settings, the compression of high-dimensional neural representations to low-dimensional binary codes is a challenging task and often require large bit-codes to be accurate. In this work, we propose a novel method for Learning Low-dimensional binary Codes (LLC) for instances as well as classes. Our method does not require any side-information, like annotated attributes or label meta-data, and learns extremely low-dimensional binary codes (~20 bits for ImageNet-1K). The learnt codes are super-efficient while still ensuring nearly optimal classification accuracy for ResNet50 on ImageNet-1K. We demonstrate that the learnt codes capture intrinsically important features in the data, by discovering an intuitive taxonomy over classes. We further quantitatively measure the quality of our codes by applying it to the efficient image retrieval as well as out-of-distribution (OOD) detection problems. For ImageNet-100 retrieval problem, our learnt binary codes outperform 16 bit HashNet using only 10 bits and also are as accurate as 10 dimensional real representations. Finally, our learnt binary codes can perform OOD detection, out-of-the-box, as accurately as a baseline that needs ~3000 samples to tune its threshold, while we require none. Code and pre-trained models are available at https://github.com/RAIVNLab/LLC.

SPECTRE: Defending Against Backdoor Attacks Using Robust Statistics

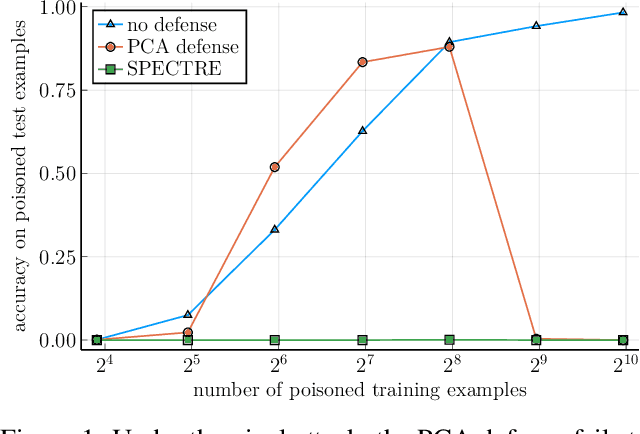
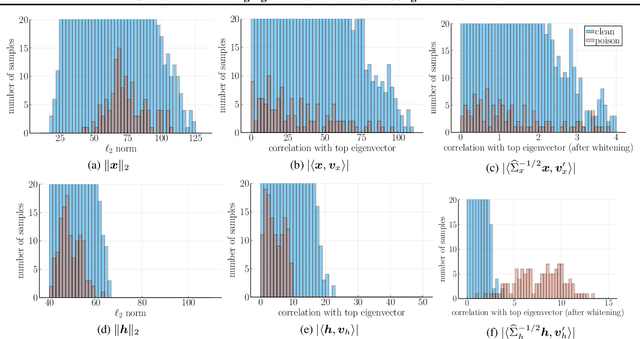
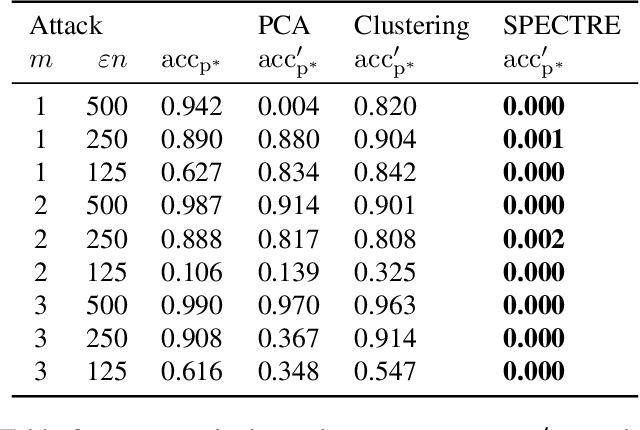
Modern machine learning increasingly requires training on a large collection of data from multiple sources, not all of which can be trusted. A particularly concerning scenario is when a small fraction of poisoned data changes the behavior of the trained model when triggered by an attacker-specified watermark. Such a compromised model will be deployed unnoticed as the model is accurate otherwise. There have been promising attempts to use the intermediate representations of such a model to separate corrupted examples from clean ones. However, these defenses work only when a certain spectral signature of the poisoned examples is large enough for detection. There is a wide range of attacks that cannot be protected against by the existing defenses. We propose a novel defense algorithm using robust covariance estimation to amplify the spectral signature of corrupted data. This defense provides a clean model, completely removing the backdoor, even in regimes where previous methods have no hope of detecting the poisoned examples. Code and pre-trained models are available at https://github.com/SewoongLab/spectre-defense .

Robust Meta-learning for Mixed Linear Regression with Small Batches

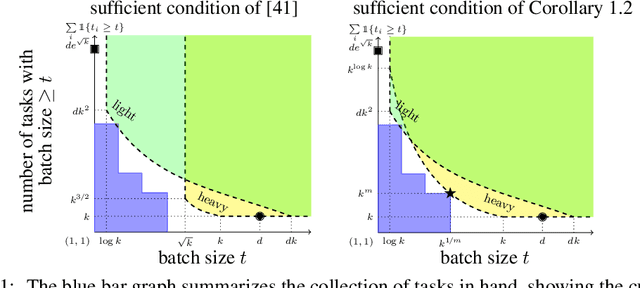
A common challenge faced in practical supervised learning, such as medical image processing and robotic interactions, is that there are plenty of tasks but each task cannot afford to collect enough labeled examples to be learned in isolation. However, by exploiting the similarities across those tasks, one can hope to overcome such data scarcity. Under a canonical scenario where each task is drawn from a mixture of k linear regressions, we study a fundamental question: can abundant small-data tasks compensate for the lack of big-data tasks? Existing second moment based approaches show that such a trade-off is efficiently achievable, with the help of medium-sized tasks with $\Omega(k^{1/2})$ examples each. However, this algorithm is brittle in two important scenarios. The predictions can be arbitrarily bad (i) even with only a few outliers in the dataset; or (ii) even if the medium-sized tasks are slightly smaller with $o(k^{1/2})$ examples each. We introduce a spectral approach that is simultaneously robust under both scenarios. To this end, we first design a novel outlier-robust principal component analysis algorithm that achieves an optimal accuracy. This is followed by a sum-of-squares algorithm to exploit the information from higher order moments. Together, this approach is robust against outliers and achieves a graceful statistical trade-off; the lack of $\Omega(k^{1/2})$-size tasks can be compensated for with smaller tasks, which can now be as small as $O(\log k)$.

Soft Threshold Weight Reparameterization for Learnable Sparsity

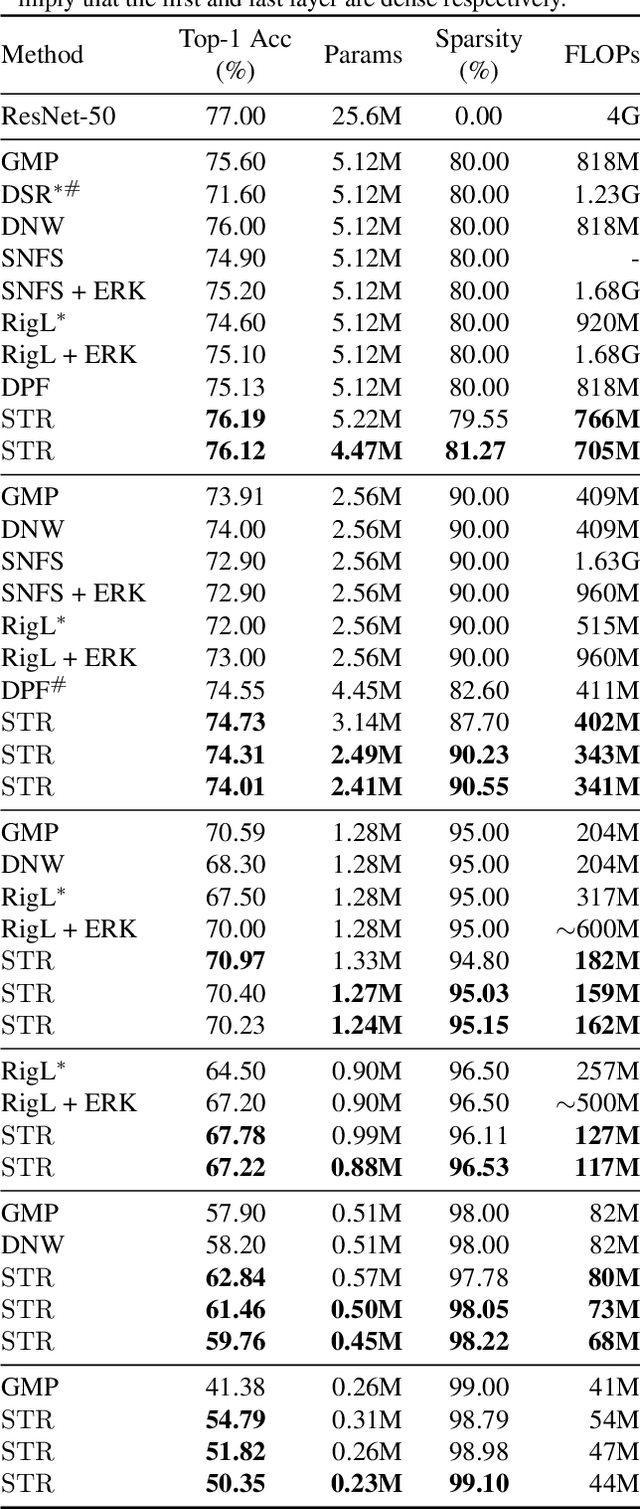
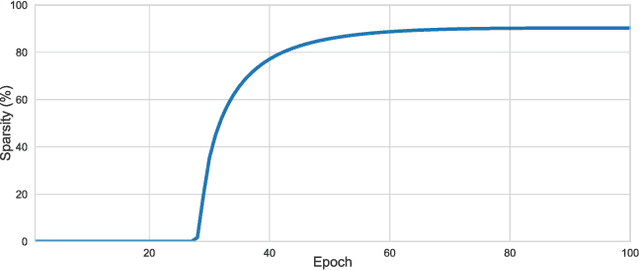
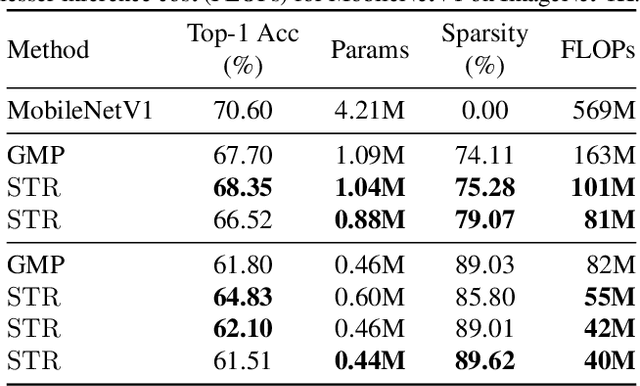
Sparsity in Deep Neural Networks (DNNs) is studied extensively with the focus of maximizing prediction accuracy given an overall parameter budget. Existing methods rely on uniform or heuristic non-uniform sparsity budgets which have sub-optimal layer-wise parameter allocation resulting in a) lower prediction accuracy or b) higher inference cost (FLOPs). This work proposes Soft Threshold Reparameterization (STR), a novel use of the soft-threshold operator on DNN weights. STR smoothly induces sparsity while learning pruning thresholds thereby obtaining a non-uniform sparsity budget. Our method achieves state-of-the-art accuracy for unstructured sparsity in CNNs (ResNet50 and MobileNetV1 on ImageNet-1K), and, additionally, learns non-uniform budgets that empirically reduce the FLOPs by up to 50%. Notably, STR boosts the accuracy over existing results by up to 10% in the ultra sparse (99%) regime and can also be used to induce low-rank (structured sparsity) in RNNs. In short, STR is a simple mechanism which learns effective sparsity budgets that contrast with popular heuristics.

Meta-learning for mixed linear regression

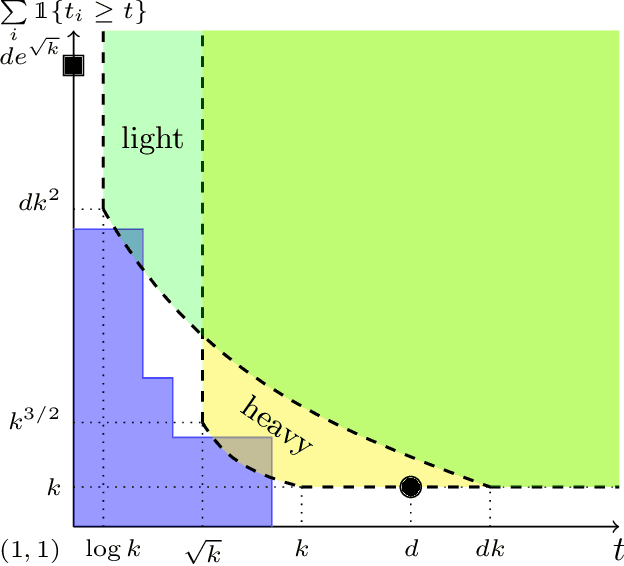
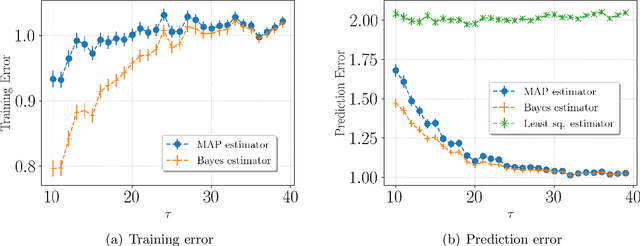
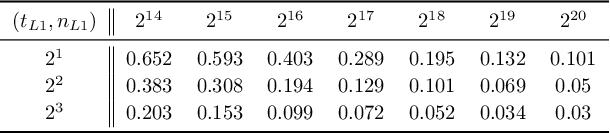
In modern supervised learning, there are a large number of tasks, but many of them are associated with only a small amount of labeled data. These include data from medical image processing and robotic interaction. Even though each individual task cannot be meaningfully trained in isolation, one seeks to meta-learn across the tasks from past experiences by exploiting some similarities. We study a fundamental question of interest: When can abundant tasks with small data compensate for lack of tasks with big data? We focus on a canonical scenario where each task is drawn from a mixture of $k$ linear regressions, and identify sufficient conditions for such a graceful exchange to hold; The total number of examples necessary with only small data tasks scales similarly as when big data tasks are available. To this end, we introduce a novel spectral approach and show that we can efficiently utilize small data tasks with the help of $\tilde\Omega(k^{3/2})$ medium data tasks each with $\tilde\Omega(k^{1/2})$ examples.

Non-Gaussianity of Stochastic Gradient Noise

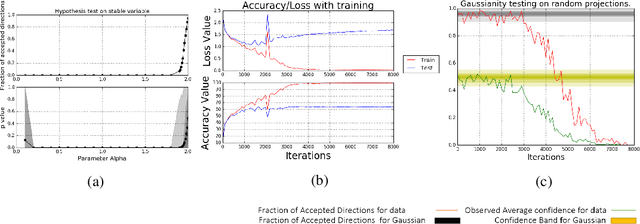
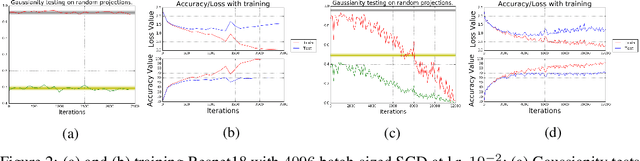
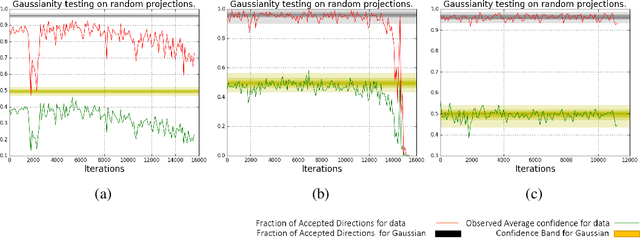
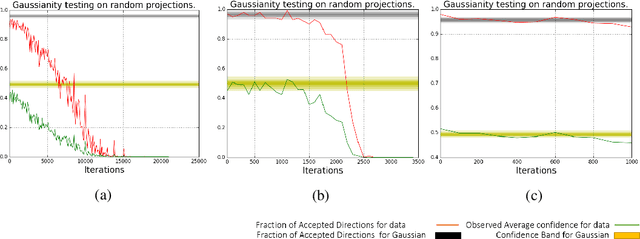
What enables Stochastic Gradient Descent (SGD) to achieve better generalization than Gradient Descent (GD) in Neural Network training? This question has attracted much attention. In this paper, we study the distribution of the Stochastic Gradient Noise (SGN) vectors during the training. We observe that for batch sizes 256 and above, the distribution is best described as Gaussian at-least in the early phases of training. This holds across data-sets, architectures, and other choices.

Clustered Monotone Transforms for Rating Factorization

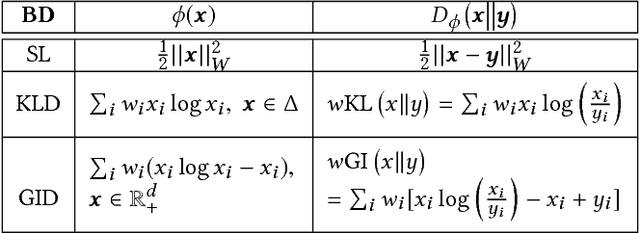
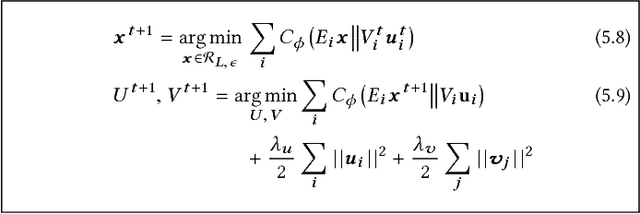
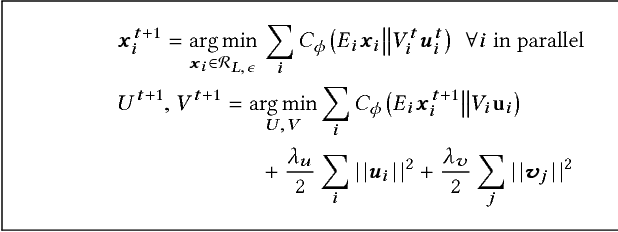
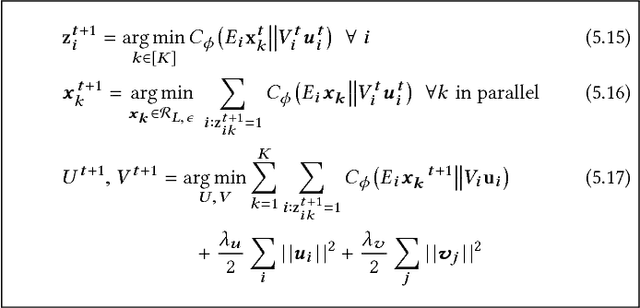
Exploiting low-rank structure of the user-item rating matrix has been the crux of many recommendation engines. However, existing recommendation engines force raters with heterogeneous behavior profiles to map their intrinsic rating scales to a common rating scale (e.g. 1-5). This non-linear transformation of the rating scale shatters the low-rank structure of the rating matrix, therefore resulting in a poor fit and consequentially, poor recommendations. In this paper, we propose Clustered Monotone Transforms for Rating Factorization (CMTRF), a novel approach to perform regression up to unknown monotonic transforms over unknown population segments. Essentially, for recommendation systems, the technique searches for monotonic transformations of the rating scales resulting in a better fit. This is combined with an underlying matrix factorization regression model that couples the user-wise ratings to exploit shared low dimensional structure. The rating scale transformations can be generated for each user, for a cluster of users, or for all the users at once, forming the basis of three simple and efficient algorithms proposed in this paper, all of which alternate between transformation of the rating scales and matrix factorization regression. Despite the non-convexity, CMTRF is theoretically shown to recover a unique solution under mild conditions. Experimental results on two synthetic and seven real-world datasets show that CMTRF outperforms other state-of-the-art baselines.