Clustered Monotone Transforms for Rating Factorization
Paper and Code
Oct 31, 2018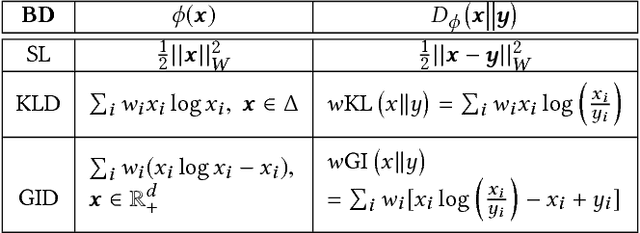
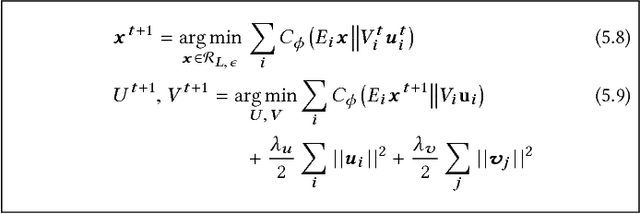
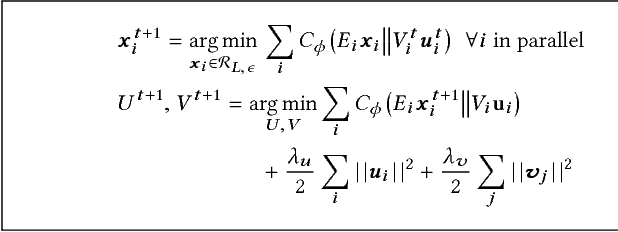
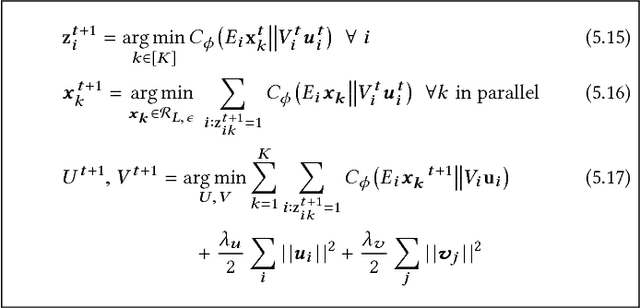
Exploiting low-rank structure of the user-item rating matrix has been the crux of many recommendation engines. However, existing recommendation engines force raters with heterogeneous behavior profiles to map their intrinsic rating scales to a common rating scale (e.g. 1-5). This non-linear transformation of the rating scale shatters the low-rank structure of the rating matrix, therefore resulting in a poor fit and consequentially, poor recommendations. In this paper, we propose Clustered Monotone Transforms for Rating Factorization (CMTRF), a novel approach to perform regression up to unknown monotonic transforms over unknown population segments. Essentially, for recommendation systems, the technique searches for monotonic transformations of the rating scales resulting in a better fit. This is combined with an underlying matrix factorization regression model that couples the user-wise ratings to exploit shared low dimensional structure. The rating scale transformations can be generated for each user, for a cluster of users, or for all the users at once, forming the basis of three simple and efficient algorithms proposed in this paper, all of which alternate between transformation of the rating scales and matrix factorization regression. Despite the non-convexity, CMTRF is theoretically shown to recover a unique solution under mild conditions. Experimental results on two synthetic and seven real-world datasets show that CMTRF outperforms other state-of-the-art baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge