Entropy contraction of the Gibbs sampler under log-concavity

The Gibbs sampler (a.k.a. Glauber dynamics and heat-bath algorithm) is a popular Markov Chain Monte Carlo algorithm which iteratively samples from the conditional distributions of a probability measure $\pi$ of interest. Under the assumption that $\pi$ is strongly log-concave, we show that the random scan Gibbs sampler contracts in relative entropy and provide a sharp characterization of the associated contraction rate. Assuming that evaluating conditionals is cheap compared to evaluating the joint density, our results imply that the number of full evaluations of $\pi$ needed for the Gibbs sampler to mix grows linearly with the condition number and is independent of the dimension. If $\pi$ is non-strongly log-concave, the convergence rate in entropy degrades from exponential to polynomial. Our techniques are versatile and extend to Metropolis-within-Gibbs schemes and the Hit-and-Run algorithm. A comparison with gradient-based schemes and the connection with the optimization literature are also discussed.

Convergence rate of random scan Coordinate Ascent Variational Inference under log-concavity

The Coordinate Ascent Variational Inference scheme is a popular algorithm used to compute the mean-field approximation of a probability distribution of interest. We analyze its random scan version, under log-concavity assumptions on the target density. Our approach builds on the recent work of M. Arnese and D. Lacker, \emph{Convergence of coordinate ascent variational inference for log-concave measures via optimal transport} [arXiv:2404.08792] which studies the deterministic scan version of the algorithm, phrasing it as a block-coordinate descent algorithm in the space of probability distributions endowed with the geometry of optimal transport. We obtain tight rates for the random scan version, which imply that the total number of factor updates required to converge scales linearly with the condition number and the number of blocks of the target distribution. By contrast, available bounds for the deterministic scan case scale quadratically in the same quantities, which is analogue to what happens for optimization of convex functions in Euclidean spaces.

Towards a mathematical theory of trajectory inference

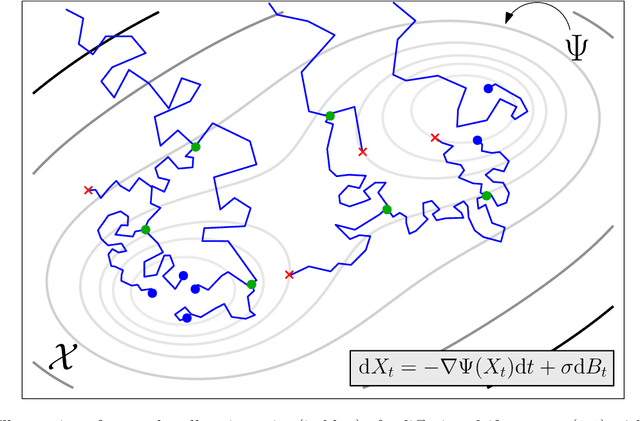
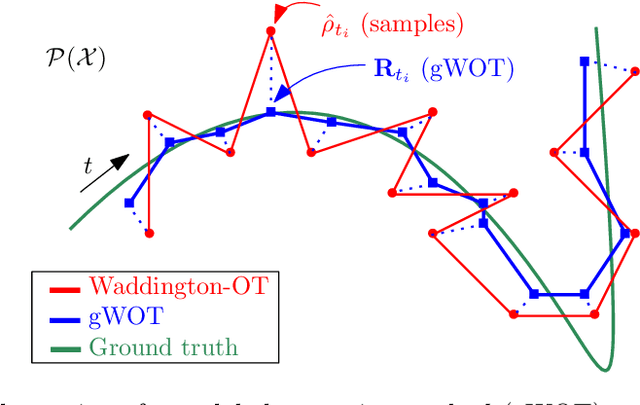
We devise a theoretical framework and a numerical method to infer trajectories of a stochastic process from snapshots of its temporal marginals. This problem arises in the analysis of single cell RNA-sequencing data, which provide high dimensional measurements of cell states but cannot track the trajectories of the cells over time. We prove that for a class of stochastic processes it is possible to recover the ground truth trajectories from limited samples of the temporal marginals at each time-point, and provide an efficient algorithm to do so in practice. The method we develop, Global Waddington-OT (gWOT), boils down to a smooth convex optimization problem posed globally over all time-points involving entropy-regularized optimal transport. We demonstrate that this problem can be solved efficiently in practice and yields good reconstructions, as we show on several synthetic and real datasets.