Beyond kNN: Adaptive, Sparse Neighborhood Graphs via Optimal Transport
Paper and Code
Aug 01, 2022
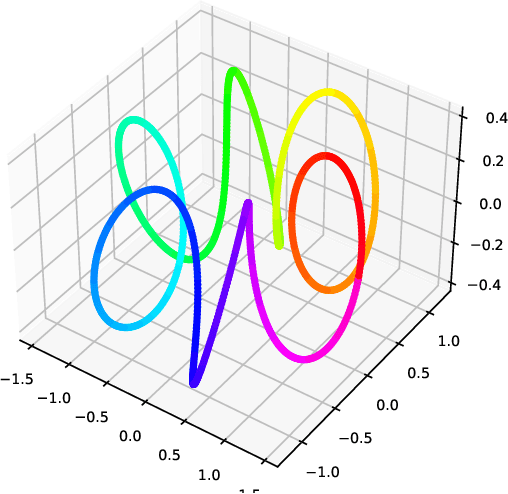
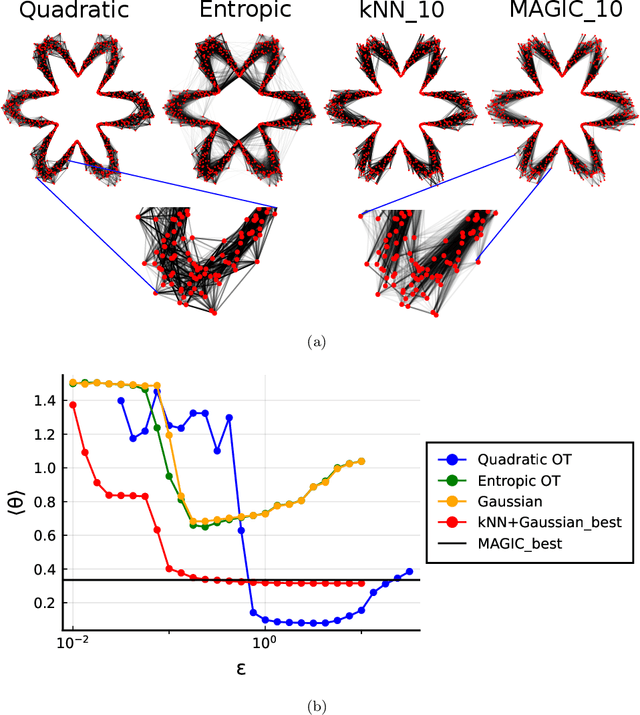
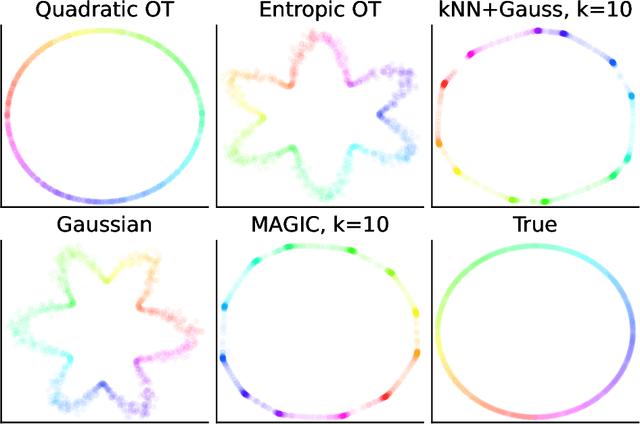
Nearest neighbour graphs are widely used to capture the geometry or topology of a dataset. One of the most common strategies to construct such a graph is based on selecting a fixed number k of nearest neighbours (kNN) for each point. However, the kNN heuristic may become inappropriate when sampling density or noise level varies across datasets. Strategies that try to get around this typically introduce additional parameters that need to be tuned. We propose a simple approach to construct an adaptive neighbourhood graph from a single parameter, based on quadratically regularised optimal transport. Our numerical experiments show that graphs constructed in this manner perform favourably in unsupervised and semi-supervised learning applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge