U-Mamba-Net: A highly efficient Mamba-based U-net style network for noisy and reverberant speech separation

The topic of speech separation involves separating mixed speech with multiple overlapping speakers into several streams, with each stream containing speech from only one speaker. Many highly effective models have emerged and proliferated rapidly over time. However, the size and computational load of these models have also increased accordingly. This is a disaster for the community, as researchers need more time and computational resources to reproduce and compare existing models. In this paper, we propose U-mamba-net: a lightweight Mamba-based U-style model for speech separation in complex environments. Mamba is a state space sequence model that incorporates feature selection capabilities. U-style network is a fully convolutional neural network whose symmetric contracting and expansive paths are able to learn multi-resolution features. In our work, Mamba serves as a feature filter, alternating with U-Net. We test the proposed model on Libri2mix. The results show that U-Mamba-Net achieves improved performance with quite low computational cost.

Developing vocal system impaired patient-aimed voice quality assessment approach using ASR representation-included multiple features

The potential of deep learning in clinical speech processing is immense, yet the hurdles of limited and imbalanced clinical data samples loom large. This article addresses these challenges by showcasing the utilization of automatic speech recognition and self-supervised learning representations, pre-trained on extensive datasets of normal speech. This innovative approach aims to estimate voice quality of patients with impaired vocal systems. Experiments involve checks on PVQD dataset, covering various causes of vocal system damage in English, and a Japanese dataset focusing on patients with Parkinson's disease before and after undergoing subthalamic nucleus deep brain stimulation (STN-DBS) surgery. The results on PVQD reveal a notable correlation (>0.8 on PCC) and an extraordinary accuracy (<0.5 on MSE) in predicting Grade, Breathy, and Asthenic indicators. Meanwhile, progress has been achieved in predicting the voice quality of patients in the context of STN-DBS.

Manifold Learning with Sparse Regularised Optimal Transport

Manifold learning is a central task in modern statistics and data science. Many datasets (cells, documents, images, molecules) can be represented as point clouds embedded in a high dimensional ambient space, however the degrees of freedom intrinsic to the data are usually far fewer than the number of ambient dimensions. The task of detecting a latent manifold along which the data are embedded is a prerequisite for a wide family of downstream analyses. Real-world datasets are subject to noisy observations and sampling, so that distilling information about the underlying manifold is a major challenge. We propose a method for manifold learning that utilises a symmetric version of optimal transport with a quadratic regularisation that constructs a sparse and adaptive affinity matrix, that can be interpreted as a generalisation of the bistochastic kernel normalisation. We prove that the resulting kernel is consistent with a Laplace-type operator in the continuous limit, establish robustness to heteroskedastic noise and exhibit these results in simulations. We identify a highly efficient computational scheme for computing this optimal transport for discrete data and demonstrate that it outperforms competing methods in a set of examples.

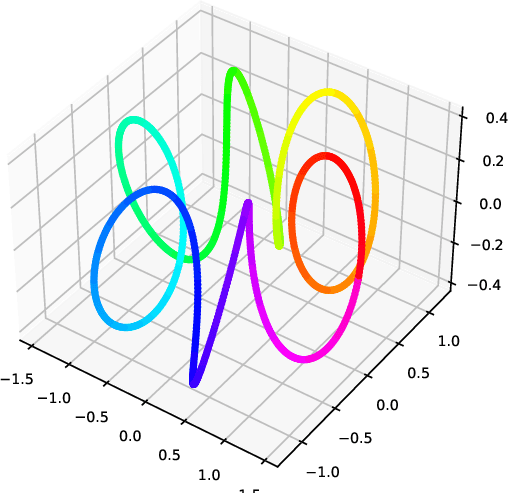
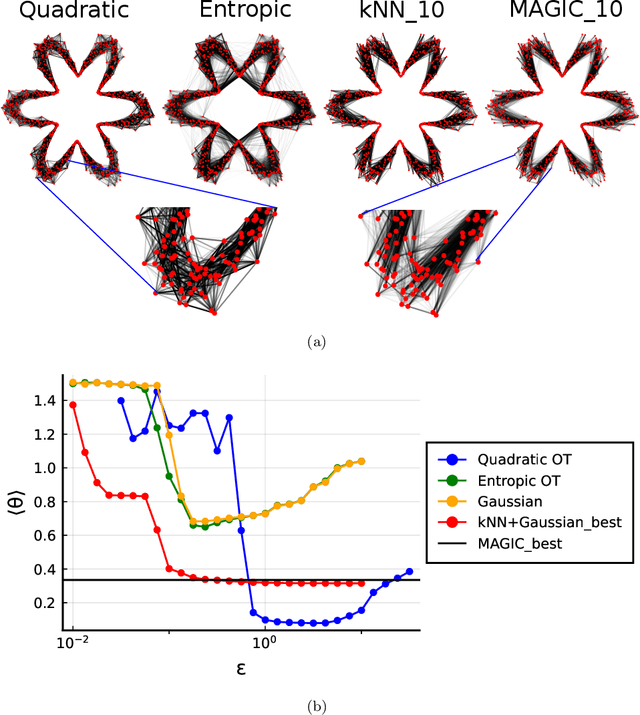
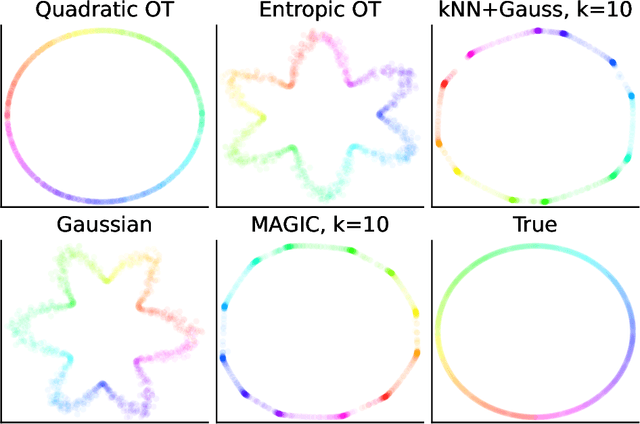
Beyond kNN: Adaptive, Sparse Neighborhood Graphs via Optimal Transport

Nearest neighbour graphs are widely used to capture the geometry or topology of a dataset. One of the most common strategies to construct such a graph is based on selecting a fixed number k of nearest neighbours (kNN) for each point. However, the kNN heuristic may become inappropriate when sampling density or noise level varies across datasets. Strategies that try to get around this typically introduce additional parameters that need to be tuned. We propose a simple approach to construct an adaptive neighbourhood graph from a single parameter, based on quadratically regularised optimal transport. Our numerical experiments show that graphs constructed in this manner perform favourably in unsupervised and semi-supervised learning applications.