Flow Gym

Flow Gym is a toolkit for research and deployment of flow-field quantification methods inspired by OpenAI Gym and Stable-Baselines3. It uses SynthPix as synthetic image generation engine and provides a unified interface for the testing, deployment and training of (learning-based) algorithms for flow-field quantification from a number of consecutive images of tracer particles. It also contains a growing number of integrations of existing algorithms and stable (re-)implementations in JAX.

Particle Image Velocimetry Refinement via Consensus ADMM

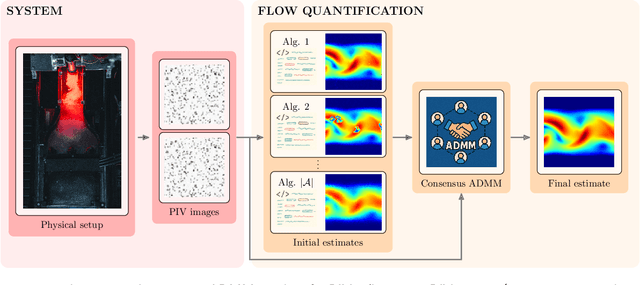
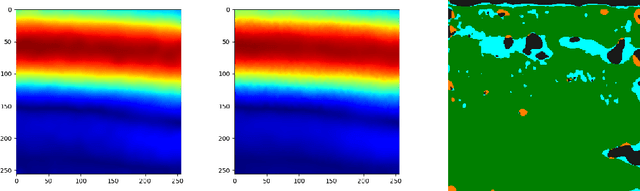
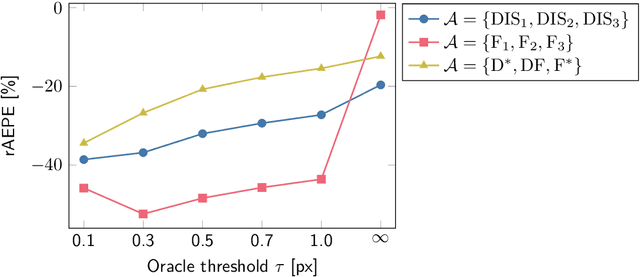
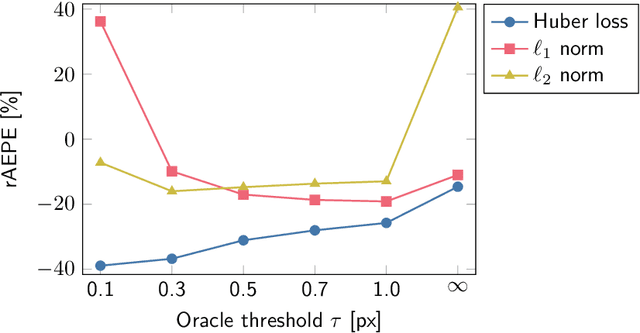
Particle Image Velocimetry (PIV) is an imaging technique in experimental fluid dynamics that quantifies flow fields around bluff bodies by analyzing the displacement of neutrally buoyant tracer particles immersed in the fluid. Traditional PIV approaches typically depend on tuning parameters specific to the imaging setup, making the performance sensitive to variations in illumination, flow conditions, and seeding density. On the other hand, even state-of-the-art machine learning methods for flow quantification are fragile outside their training set. In our experiments, we observed that flow quantification would improve if different tunings (or algorithms) were applied to different regions of the same image pair. In this work, we parallelize the instantaneous flow quantification with multiple algorithms and adopt a consensus framework based on the alternating direction method of multipliers, seamlessly incorporating priors such as smoothness and incompressibility. We perform several numerical experiments to demonstrate the benefits of this approach. For instance, we achieve a decrease in end-point-error of up to 20% of a dense-inverse-search estimator at an inference rate of 60Hz, and we show how this performance boost can be increased further with outlier rejection. Our method is implemented in JAX, effectively exploiting hardware acceleration, and integrated in Flow Gym, enabling (i) reproducible comparisons with the state-of-the-art, (ii) testing different base algorithms, (iii) straightforward deployment for active fluids control applications.

SynthPix: A lightspeed PIV images generator

We describe SynthPix, a synthetic image generator for Particle Image Velocimetry (PIV) with a focus on performance and parallelism on accelerators, implemented in JAX. SynthPix supports the same configuration parameters as existing tools but achieves a throughput several orders of magnitude higher in image-pair generation per second. SynthPix was developed to enable the training of data-hungry reinforcement learning methods for flow estimation and for reducing the iteration times during the development of fast flow estimation methods used in recent active fluids control studies with real-time PIV feedback. We believe SynthPix to be useful for the fluid dynamics community, and in this paper we describe the main ideas behind this software package.

Using reinforcement learning to probe the role of feedback in skill acquisition

Many high-performance human activities are executed with little or no external feedback: think of a figure skater landing a triple jump, a pitcher throwing a curveball for a strike, or a barista pouring latte art. To study the process of skill acquisition under fully controlled conditions, we bypass human subjects. Instead, we directly interface a generalist reinforcement learning agent with a spinning cylinder in a tabletop circulating water channel to maximize or minimize drag. This setup has several desirable properties. First, it is a physical system, with the rich interactions and complex dynamics that only the physical world has: the flow is highly chaotic and extremely difficult, if not impossible, to model or simulate accurately. Second, the objective -- drag minimization or maximization -- is easy to state and can be captured directly in the reward, yet good strategies are not obvious beforehand. Third, decades-old experimental studies provide recipes for simple, high-performance open-loop policies. Finally, the setup is inexpensive and far easier to reproduce than human studies. In our experiments we find that high-dimensional flow feedback lets the agent discover high-performance drag-control strategies with only minutes of real-world interaction. When we later replay the same action sequences without any feedback, we obtain almost identical performance. This shows that feedback, and in particular flow feedback, is not needed to execute the learned policy. Surprisingly, without flow feedback during training the agent fails to discover any well-performing policy in drag maximization, but still succeeds in drag minimization, albeit more slowly and less reliably. Our studies show that learning a high-performance skill can require richer information than executing it, and learning conditions can be kind or wicked depending solely on the goal, not on dynamics or policy complexity.

Langevin SDEs have unique transient dynamics

The overdamped Langevin stochastic differential equation (SDE) is a classical physical model used for chemical, genetic, and hydrological dynamics. In this work, we prove that the drift and diffusion terms of a Langevin SDE are jointly identifiable from temporal marginal distributions if and only if the process is observed out of equilibrium. This complete characterization of structural identifiability removes the long-standing assumption that the diffusion must be known to identify the drift. We then complement our theory with experiments in the finite sample setting and study the practical identifiability of the drift and diffusion, in order to propose heuristics for optimal data collection.

Energy Matching: Unifying Flow Matching and Energy-Based Models for Generative Modeling

Generative models often map noise to data by matching flows or scores, but these approaches become cumbersome for incorporating partial observations or additional priors. Inspired by recent advances in Wasserstein gradient flows, we propose Energy Matching, a framework that unifies flow-based approaches with the flexibility of energy-based models (EBMs). Far from the data manifold, samples move along curl-free, optimal transport paths from noise to data. As they approach the data manifold, an entropic energy term guides the system into a Boltzmann equilibrium distribution, explicitly capturing the underlying likelihood structure of the data. We parameterize this dynamic with a single time-independent scalar field, which serves as both a powerful generator and a flexible prior for effective regularization of inverse problems. Our method substantially outperforms existing EBMs on CIFAR-10 generation (FID 3.97 compared to 8.61), while retaining the simulation-free training of transport-based approaches away from the data manifold. Additionally, we exploit the flexibility of our method and introduce an interaction energy for diverse mode exploration. Our approach focuses on learning a static scalar potential energy -- without time conditioning, auxiliary generators, or additional networks -- marking a significant departure from recent EBM methods. We believe this simplified framework significantly advances EBM capabilities and paves the way for their broader adoption in generative modeling across diverse domains.

Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

Learning Diffusion at Lightspeed

Diffusion regulates a phenomenal number of natural processes and the dynamics of many successful generative models. Existing models to learn the diffusion terms from observational data rely on complex bilevel optimization problems and properly model only the drift of the system. We propose a new simple model, JKOnet*, which bypasses altogether the complexity of existing architectures while presenting significantly enhanced representational capacity: JKOnet* recovers the potential, interaction, and internal energy components of the underlying diffusion process. JKOnet* minimizes a simple quadratic loss, runs at lightspeed, and drastically outperforms other baselines in practice. Additionally, JKOnet* provides a closed-form optimal solution for linearly parametrized functionals. Our methodology is based on the interpretation of diffusion processes as energy-minimizing trajectories in the probability space via the so-called JKO scheme, which we study via its first-order optimality conditions, in light of few-weeks-old advancements in optimization in the probability space.