Learn to Bid as a Price-Maker Wind Power Producer

Wind power producers (WPPs) participating in short-term power markets face significant imbalance costs due to their non-dispatchable and variable production. While some WPPs have a large enough market share to influence prices with their bidding decisions, existing optimal bidding methods rarely account for this aspect. Price-maker approaches typically model bidding as a bilevel optimization problem, but these methods require complex market models, estimating other participants' actions, and are computationally demanding. To address these challenges, we propose an online learning algorithm that leverages contextual information to optimize WPP bids in the price-maker setting. We formulate the strategic bidding problem as a contextual multi-armed bandit, ensuring provable regret minimization. The algorithm's performance is evaluated against various benchmark strategies using a numerical simulation of the German day-ahead and real-time markets.

Decision-Dependent Stochastic Optimization: The Role of Distribution Dynamics

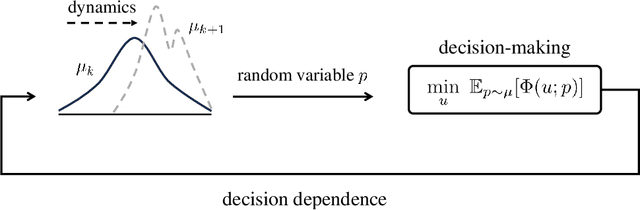
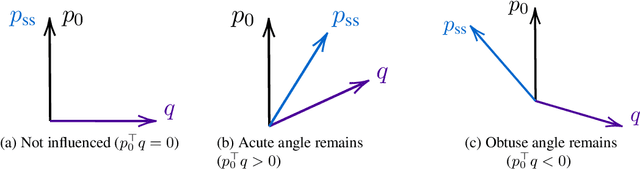
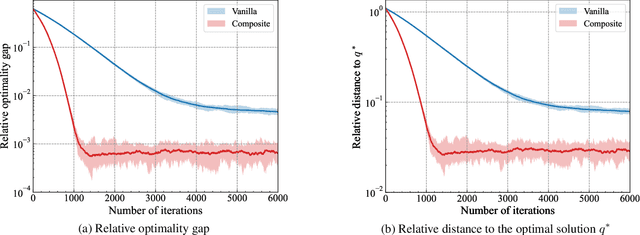
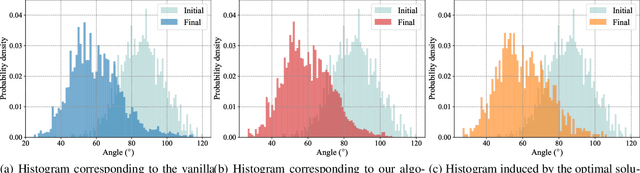
Distribution shifts have long been regarded as troublesome external forces that a decision-maker should either counteract or conform to. An intriguing feedback phenomenon termed decision dependence arises when the deployed decision affects the environment and alters the data-generating distribution. In the realm of performative prediction, this is encoded by distribution maps parameterized by decisions due to strategic behaviors. In contrast, we formalize an endogenous distribution shift as a feedback process featuring nonlinear dynamics that couple the evolving distribution with the decision. Stochastic optimization in this dynamic regime provides a fertile ground to examine the various roles played by dynamics in the composite problem structure. To this end, we develop an online algorithm that achieves optimal decision-making by both adapting to and shaping the dynamic distribution. Throughout the paper, we adopt a distributional perspective and demonstrate how this view facilitates characterizations of distribution dynamics and the optimality and generalization performance of the proposed algorithm. We showcase the theoretical results in an opinion dynamics context, where an opportunistic party maximizes the affinity of a dynamic polarized population, and in a recommender system scenario, featuring performance optimization with discrete distributions in the probability simplex.

An Adaptive Data-Enabled Policy Optimization Approach for Autonomous Bicycle Control

This paper presents a unified control framework that integrates a Feedback Linearization (FL) controller in the inner loop with an adaptive Data-Enabled Policy Optimization (DeePO) controller in the outer loop to balance an autonomous bicycle. While the FL controller stabilizes and partially linearizes the inherently unstable and nonlinear system, its performance is compromised by unmodeled dynamics and time-varying characteristics. To overcome these limitations, the DeePO controller is introduced to enhance adaptability and robustness. The initial control policy of DeePO is obtained from a finite set of offline, persistently exciting input and state data. To improve stability and compensate for system nonlinearities and disturbances, a robustness-promoting regularizer refines the initial policy, while the adaptive section of the DeePO framework is enhanced with a forgetting factor to improve adaptation to time-varying dynamics. The proposed DeePO+FL approach is evaluated through simulations and real-world experiments on an instrumented autonomous bicycle. Results demonstrate its superiority over the FL-only approach, achieving more precise tracking of the reference lean angle and lean rate.

Contractivity and linear convergence in bilinear saddle-point problems: An operator-theoretic approach

We study the convex-concave bilinear saddle-point problem $\min_x \max_y f(x) + y^\top Ax - g(y)$, where both, only one, or none of the functions $f$ and $g$ are strongly convex, and suitable rank conditions on the matrix $A$ hold. The solution of this problem is at the core of many machine learning tasks. By employing tools from operator theory, we systematically prove the contractivity (in turn, the linear convergence) of several first-order primal-dual algorithms, including the Chambolle-Pock method. Our approach results in concise and elegant proofs, and it yields new convergence guarantees and tighter bounds compared to known results.

Maximum likelihood inference for high-dimensional problems with multiaffine variable relations

Maximum Likelihood Estimation of continuous variable models can be very challenging in high dimensions, due to potentially complex probability distributions. The existence of multiple interdependencies among variables can make it very difficult to establish convergence guarantees. This leads to a wide use of brute-force methods, such as grid searching and Monte-Carlo sampling and, when applicable, complex and problem-specific algorithms. In this paper, we consider inference problems where the variables are related by multiaffine expressions. We propose a novel Alternating and Iteratively-Reweighted Least Squares (AIRLS) algorithm, and prove its convergence for problems with Generalized Normal Distributions. We also provide an efficient method to compute the variance of the estimates obtained using AIRLS. Finally, we show how the method can be applied to graphical statistical models. We perform numerical experiments on several inference problems, showing significantly better performance than state-of-the-art approaches in terms of scalability, robustness to noise, and convergence speed due to an empirically observed super-linear convergence rate.

Learning Diffusion at Lightspeed

Diffusion regulates a phenomenal number of natural processes and the dynamics of many successful generative models. Existing models to learn the diffusion terms from observational data rely on complex bilevel optimization problems and properly model only the drift of the system. We propose a new simple model, JKOnet*, which bypasses altogether the complexity of existing architectures while presenting significantly enhanced representational capacity: JKOnet* recovers the potential, interaction, and internal energy components of the underlying diffusion process. JKOnet* minimizes a simple quadratic loss, runs at lightspeed, and drastically outperforms other baselines in practice. Additionally, JKOnet* provides a closed-form optimal solution for linearly parametrized functionals. Our methodology is based on the interpretation of diffusion processes as energy-minimizing trajectories in the probability space via the so-called JKO scheme, which we study via its first-order optimality conditions, in light of few-weeks-old advancements in optimization in the probability space.

NeoRL: Efficient Exploration for Nonepisodic RL

We study the problem of nonepisodic reinforcement learning (RL) for nonlinear dynamical systems, where the system dynamics are unknown and the RL agent has to learn from a single trajectory, i.e., without resets. We propose Nonepisodic Optimistic RL (NeoRL), an approach based on the principle of optimism in the face of uncertainty. NeoRL uses well-calibrated probabilistic models and plans optimistically w.r.t. the epistemic uncertainty about the unknown dynamics. Under continuity and bounded energy assumptions on the system, we provide a first-of-its-kind regret bound of $\setO(\beta_T \sqrt{T \Gamma_T})$ for general nonlinear systems with Gaussian process dynamics. We compare NeoRL to other baselines on several deep RL environments and empirically demonstrate that NeoRL achieves the optimal average cost while incurring the least regret.

When to Sense and Control? A Time-adaptive Approach for Continuous-Time RL

Reinforcement learning (RL) excels in optimizing policies for discrete-time Markov decision processes (MDP). However, various systems are inherently continuous in time, making discrete-time MDPs an inexact modeling choice. In many applications, such as greenhouse control or medical treatments, each interaction (measurement or switching of action) involves manual intervention and thus is inherently costly. Therefore, we generally prefer a time-adaptive approach with fewer interactions with the system. In this work, we formalize an RL framework, Time-adaptive Control & Sensing (TaCoS), that tackles this challenge by optimizing over policies that besides control predict the duration of its application. Our formulation results in an extended MDP that any standard RL algorithm can solve. We demonstrate that state-of-the-art RL algorithms trained on TaCoS drastically reduce the interaction amount over their discrete-time counterpart while retaining the same or improved performance, and exhibiting robustness over discretization frequency. Finally, we propose OTaCoS, an efficient model-based algorithm for our setting. We show that OTaCoS enjoys sublinear regret for systems with sufficiently smooth dynamics and empirically results in further sample-efficiency gains.

Bridging the Sim-to-Real Gap with Bayesian Inference

We present SIM-FSVGD for learning robot dynamics from data. As opposed to traditional methods, SIM-FSVGD leverages low-fidelity physical priors, e.g., in the form of simulators, to regularize the training of neural network models. While learning accurate dynamics already in the low data regime, SIM-FSVGD scales and excels also when more data is available. We empirically show that learning with implicit physical priors results in accurate mean model estimation as well as precise uncertainty quantification. We demonstrate the effectiveness of SIM-FSVGD in bridging the sim-to-real gap on a high-performance RC racecar system. Using model-based RL, we demonstrate a highly dynamic parking maneuver with drifting, using less than half the data compared to the state of the art.

Towards a Systems Theory of Algorithms

Traditionally, numerical algorithms are seen as isolated pieces of code confined to an {\em in silico} existence. However, this perspective is not appropriate for many modern computational approaches in control, learning, or optimization, wherein {\em in vivo} algorithms interact with their environment. Examples of such {\em open} include various real-time optimization-based control strategies, reinforcement learning, decision-making architectures, online optimization, and many more. Further, even {\em closed} algorithms in learning or optimization are increasingly abstracted in block diagrams with interacting dynamic modules and pipelines. In this opinion paper, we state our vision on a to-be-cultivated {\em systems theory of algorithms} and argue in favour of viewing algorithms as open dynamical systems interacting with other algorithms, physical systems, humans, or databases. Remarkably, the manifold tools developed under the umbrella of systems theory also provide valuable insights into this burgeoning paradigm shift and its accompanying challenges in the algorithmic world. We survey various instances where the principles of algorithmic systems theory are being developed and outline pertinent modeling, analysis, and design challenges.