An Adaptive Data-Enabled Policy Optimization Approach for Autonomous Bicycle Control

This paper presents a unified control framework that integrates a Feedback Linearization (FL) controller in the inner loop with an adaptive Data-Enabled Policy Optimization (DeePO) controller in the outer loop to balance an autonomous bicycle. While the FL controller stabilizes and partially linearizes the inherently unstable and nonlinear system, its performance is compromised by unmodeled dynamics and time-varying characteristics. To overcome these limitations, the DeePO controller is introduced to enhance adaptability and robustness. The initial control policy of DeePO is obtained from a finite set of offline, persistently exciting input and state data. To improve stability and compensate for system nonlinearities and disturbances, a robustness-promoting regularizer refines the initial policy, while the adaptive section of the DeePO framework is enhanced with a forgetting factor to improve adaptation to time-varying dynamics. The proposed DeePO+FL approach is evaluated through simulations and real-world experiments on an instrumented autonomous bicycle. Results demonstrate its superiority over the FL-only approach, achieving more precise tracking of the reference lean angle and lean rate.

Primal-dual Learning for the Model-free Risk-constrained Linear Quadratic Regulator

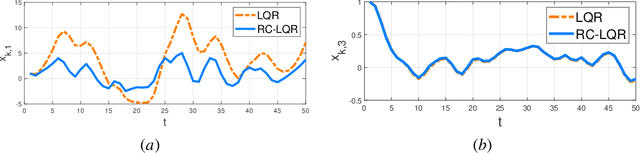
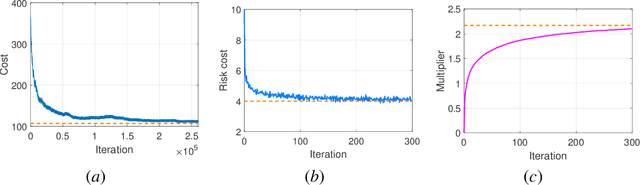
Risk-aware control, though with promise to tackle unexpected events, requires a known exact dynamical model. In this work, we propose a model-free framework to learn a risk-aware controller with a focus on the linear system. We formulate it as a discrete-time infinite-horizon LQR problem with a state predictive variance constraint. To solve it, we parameterize the policy with a feedback gain pair and leverage primal-dual methods to optimize it by solely using data. We first study the optimization landscape of the Lagrangian function and establish the strong duality in spite of its non-convex nature. Alongside, we find that the Lagrangian function enjoys an important local gradient dominance property, which is then exploited to develop a convergent random search algorithm to learn the dual function. Furthermore, we propose a primal-dual algorithm with global convergence to learn the optimal policy-multiplier pair. Finally, we validate our results via simulations.