Towards a Systems Theory of Algorithms

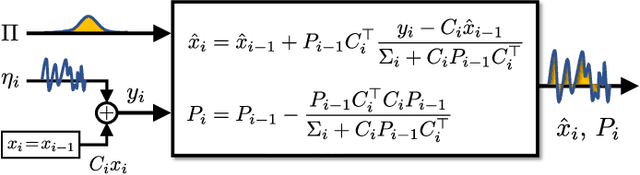
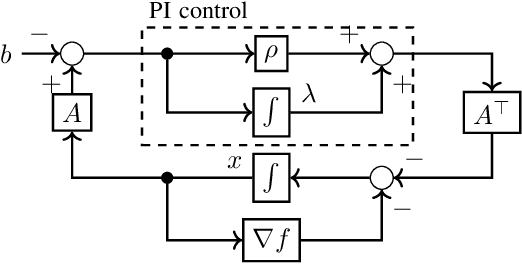
Traditionally, numerical algorithms are seen as isolated pieces of code confined to an {\em in silico} existence. However, this perspective is not appropriate for many modern computational approaches in control, learning, or optimization, wherein {\em in vivo} algorithms interact with their environment. Examples of such {\em open} include various real-time optimization-based control strategies, reinforcement learning, decision-making architectures, online optimization, and many more. Further, even {\em closed} algorithms in learning or optimization are increasingly abstracted in block diagrams with interacting dynamic modules and pipelines. In this opinion paper, we state our vision on a to-be-cultivated {\em systems theory of algorithms} and argue in favour of viewing algorithms as open dynamical systems interacting with other algorithms, physical systems, humans, or databases. Remarkably, the manifold tools developed under the umbrella of systems theory also provide valuable insights into this burgeoning paradigm shift and its accompanying challenges in the algorithmic world. We survey various instances where the principles of algorithmic systems theory are being developed and outline pertinent modeling, analysis, and design challenges.

Designing Optimal Personalized Incentive for Traffic Routing using BIG Hype algorithm

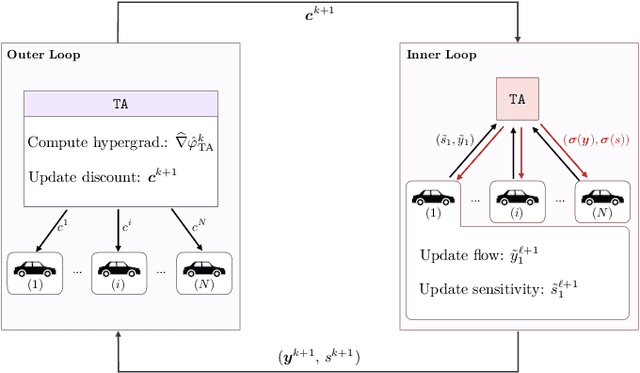
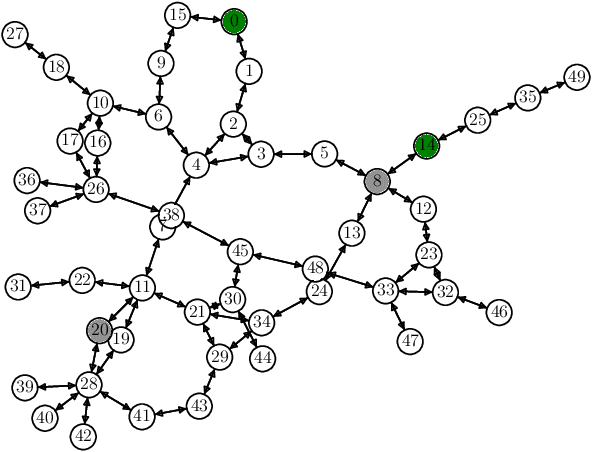
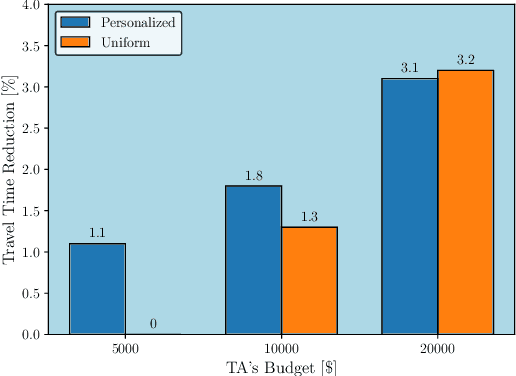
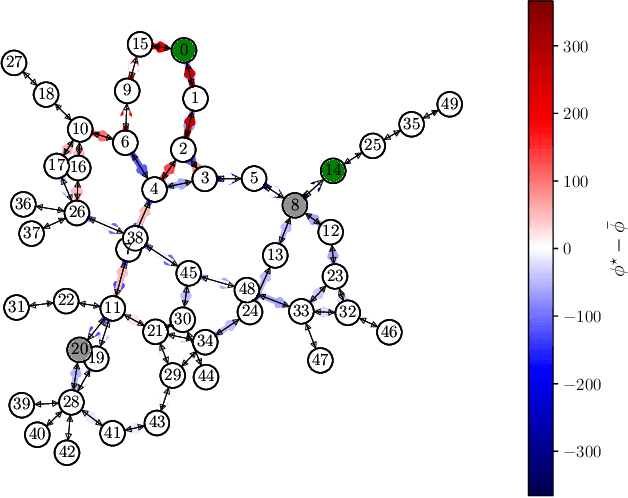
We study the problem of optimally routing plug-in electric and conventional fuel vehicles on a city level. In our model, commuters selfishly aim to minimize a local cost that combines travel time, from a fixed origin to a desired destination, and the monetary cost of using city facilities, parking or service stations. The traffic authority can influence the commuters' preferred routing choice by means of personalized discounts on parking tickets and on the energy price at service stations. We formalize the problem of designing these monetary incentives optimally as a large-scale bilevel game, where constraints arise at both levels due to the finite capacities of city facilities and incentives budget. Then, we develop an efficient decentralized solution scheme with convergence guarantees based on BIG Hype, a recently-proposed hypergradient-based algorithm for hierarchical games. Finally, we validate our model via numerical simulations over the Anaheim's network, and show that the proposed approach produces sensible results in terms of traffic decongestion and it is able to solve in minutes problems with more than 48000 variables and 110000 constraints.

Stability and Robustness of Distributed Suboptimal Model Predictive Control

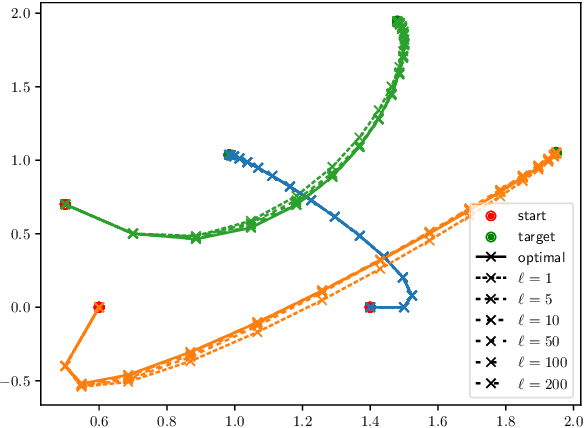
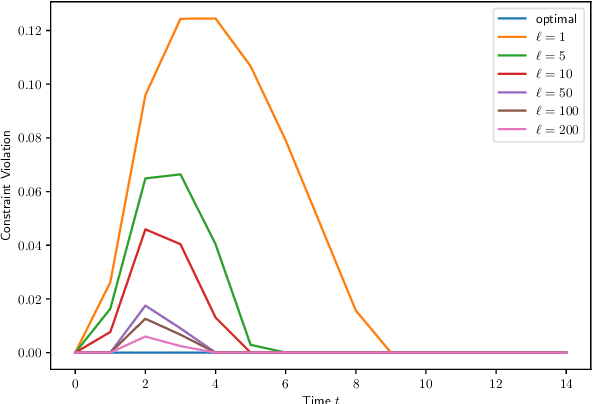
In distributed model predictive control (MPC), the control input at each sampling time is computed by solving a large-scale optimal control problem (OCP) over a finite horizon using distributed algorithms. Typically, such algorithms require several (virtually, infinite) communication rounds between the subsystems to converge, which is a major drawback both computationally and from an energetic perspective (for wireless systems). Motivated by these challenges, we propose a suboptimal distributed MPC scheme in which the total communication burden is distributed also in time, by maintaining a running solution estimate for the large-scale OCP and updating it at each sampling time. We demonstrate that, under some regularity conditions, the resulting suboptimal MPC control law recovers the qualitative robust stability properties of optimal MPC, if the communication budget at each sampling time is large enough.