Saverio Bolognani
Decision-Dependent Stochastic Optimization: The Role of Distribution Dynamics
Mar 10, 2025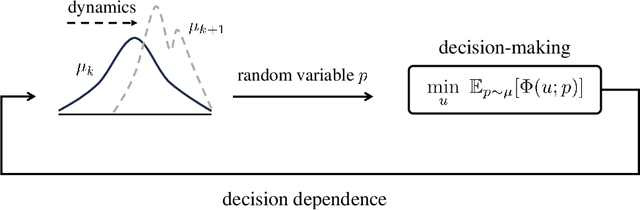
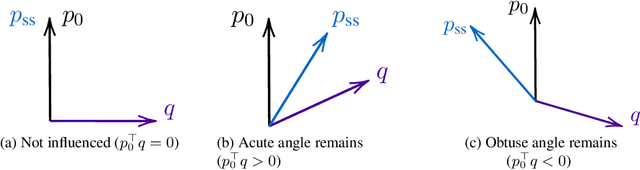
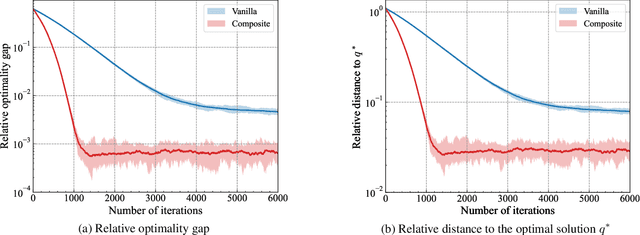
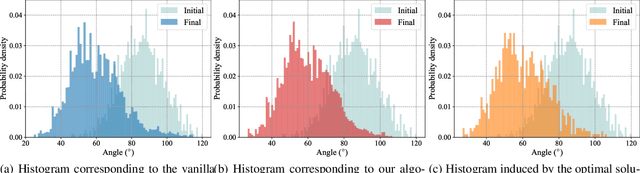
Abstract:Distribution shifts have long been regarded as troublesome external forces that a decision-maker should either counteract or conform to. An intriguing feedback phenomenon termed decision dependence arises when the deployed decision affects the environment and alters the data-generating distribution. In the realm of performative prediction, this is encoded by distribution maps parameterized by decisions due to strategic behaviors. In contrast, we formalize an endogenous distribution shift as a feedback process featuring nonlinear dynamics that couple the evolving distribution with the decision. Stochastic optimization in this dynamic regime provides a fertile ground to examine the various roles played by dynamics in the composite problem structure. To this end, we develop an online algorithm that achieves optimal decision-making by both adapting to and shaping the dynamic distribution. Throughout the paper, we adopt a distributional perspective and demonstrate how this view facilitates characterizations of distribution dynamics and the optimality and generalization performance of the proposed algorithm. We showcase the theoretical results in an opinion dynamics context, where an opportunistic party maximizes the affinity of a dynamic polarized population, and in a recommender system scenario, featuring performance optimization with discrete distributions in the probability simplex.
Towards a Systems Theory of Algorithms
Jan 25, 2024
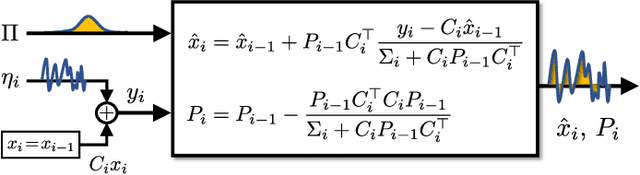
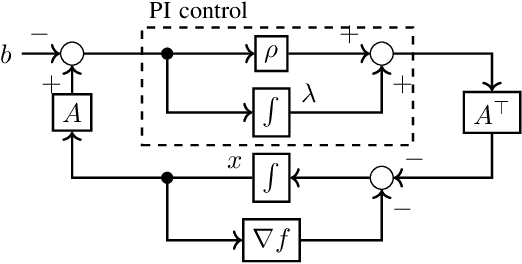

Abstract:Traditionally, numerical algorithms are seen as isolated pieces of code confined to an {\em in silico} existence. However, this perspective is not appropriate for many modern computational approaches in control, learning, or optimization, wherein {\em in vivo} algorithms interact with their environment. Examples of such {\em open} include various real-time optimization-based control strategies, reinforcement learning, decision-making architectures, online optimization, and many more. Further, even {\em closed} algorithms in learning or optimization are increasingly abstracted in block diagrams with interacting dynamic modules and pipelines. In this opinion paper, we state our vision on a to-be-cultivated {\em systems theory of algorithms} and argue in favour of viewing algorithms as open dynamical systems interacting with other algorithms, physical systems, humans, or databases. Remarkably, the manifold tools developed under the umbrella of systems theory also provide valuable insights into this burgeoning paradigm shift and its accompanying challenges in the algorithmic world. We survey various instances where the principles of algorithmic systems theory are being developed and outline pertinent modeling, analysis, and design challenges.
A Classification of Feedback Loops and Their Relation to Biases in Automated Decision-Making Systems
May 10, 2023Abstract:Prediction-based decision-making systems are becoming increasingly prevalent in various domains. Previous studies have demonstrated that such systems are vulnerable to runaway feedback loops, e.g., when police are repeatedly sent back to the same neighborhoods regardless of the actual rate of criminal activity, which exacerbate existing biases. In practice, the automated decisions have dynamic feedback effects on the system itself that can perpetuate over time, making it difficult for short-sighted design choices to control the system's evolution. While researchers started proposing longer-term solutions to prevent adverse outcomes (such as bias towards certain groups), these interventions largely depend on ad hoc modeling assumptions and a rigorous theoretical understanding of the feedback dynamics in ML-based decision-making systems is currently missing. In this paper, we use the language of dynamical systems theory, a branch of applied mathematics that deals with the analysis of the interconnection of systems with dynamic behaviors, to rigorously classify the different types of feedback loops in the ML-based decision-making pipeline. By reviewing existing scholarly work, we show that this classification covers many examples discussed in the algorithmic fairness community, thereby providing a unifying and principled framework to study feedback loops. By qualitative analysis, and through a simulation example of recommender systems, we show which specific types of ML biases are affected by each type of feedback loop. We find that the existence of feedback loops in the ML-based decision-making pipeline can perpetuate, reinforce, or even reduce ML biases.
How Bad is Selfish Driving? Bounding the Inefficiency of Equilibria in Urban Driving Games
Oct 24, 2022Abstract:We consider the interaction among agents engaging in a driving task and we model it as general-sum game. This class of games exhibits a plurality of different equilibria posing the issue of equilibrium selection. While selecting the most efficient equilibrium (in term of social cost) is often impractical from a computational standpoint, in this work we study the (in)efficiency of any equilibrium players might agree to play. More specifically, we bound the equilibrium inefficiency by modeling driving games as particular type of congestion games over spatio-temporal resources. We obtain novel guarantees that refine existing bounds on the Price of Anarchy (PoA) as a function of problem-dependent game parameters. For instance, the relative trade-off between proximity costs and personal objectives such as comfort and progress. Although the obtained guarantees concern open-loop trajectories, we observe efficient equilibria even when agents employ closed-loop policies trained via decentralized multi-agent reinforcement learning.
Posetal Games: Efficiency, Existence, and Refinement of Equilibria in Games with Prioritized Metrics
Nov 13, 2021



Abstract:Modern applications require robots to comply with multiple, often conflicting rules and to interact with the other agents. We present Posetal Games as a class of games in which each player expresses a preference over the outcomes via a partially ordered set of metrics. This allows one to combine hierarchical priorities of each player with the interactive nature of the environment. By contextualizing standard game theoretical notions, we provide two sufficient conditions on the preference of the players to prove existence of pure Nash Equilibria in finite action sets. Moreover, we define formal operations on the preference structures and link them to a refinement of the game solutions, showing how the set of equilibria can be systematically shrunk. The presented results are showcased in a driving game where autonomous vehicles select from a finite set of trajectories. The results demonstrate the interpretability of results in terms of minimum-rank-violation for each player.
Today Me, Tomorrow Thee: Efficient Resource Allocation in Competitive Settings using Karma Games
Jul 22, 2019



Abstract:We present a new type of coordination mechanism among multiple agents for the allocation of a finite resource, such as the allocation of time slots for passing an intersection. We consider the setting where we associate one counter to each agent, which we call karma value, and where there is an established mechanism to decide resource allocation based on agents exchanging karma. The idea is that agents might be inclined to pass on using resources today, in exchange for karma, which will make it easier for them to claim the resource use in the future. To understand whether such a system might work robustly, we only design the protocol and not the agents' policies. We take a game-theoretic perspective and compute policies corresponding to Nash equilibria for the game. We find, surprisingly, that the Nash equilibria for a society of self-interested agents are very close in social welfare to a centralized cooperative solution. These results suggest that many resource allocation problems can have a simple, elegant, and robust solution, assuming the availability of a karma accounting mechanism.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge