Optimization of Rulebooks via Asymptotically Representing Lexicographic Hierarchies for Autonomous Vehicles

A key challenge in autonomous driving is that Autonomous Vehicles (AVs) must contend with multiple, often conflicting, planning requirements. These requirements naturally form in a hierarchy -- e.g., avoiding a collision is more important than maintaining lane. While the exact structure of this hierarchy remains unknown, to progress towards ensuring that AVs satisfy pre-determined behavior specifications, it is crucial to develop approaches that systematically account for it. Motivated by lexicographic behavior specification in AVs, this work addresses a lexicographic multi-objective motion planning problem, where each objective is incomparably more important than the next -- consider that avoiding a collision is incomparably more important than a lane change violation. This work ties together two elements. Firstly, a multi-objective candidate function that asymptotically represents lexicographic orders is introduced. Unlike existing multi-objective cost function formulations, this approach assures that returned solutions asymptotically align with the lexicographic behavior specification. Secondly, inspired by continuation methods, we propose two algorithms that asymptotically approach minimum rank decisions -- i.e., decisions that satisfy the highest number of important rules possible. Through a couple practical examples, we showcase that the proposed candidate function asymptotically represents the lexicographic hierarchy, and that both proposed algorithms return minimum rank decisions, even when other approaches do not.

Tactical Game-theoretic Decision-making with Homotopy Class Constraints

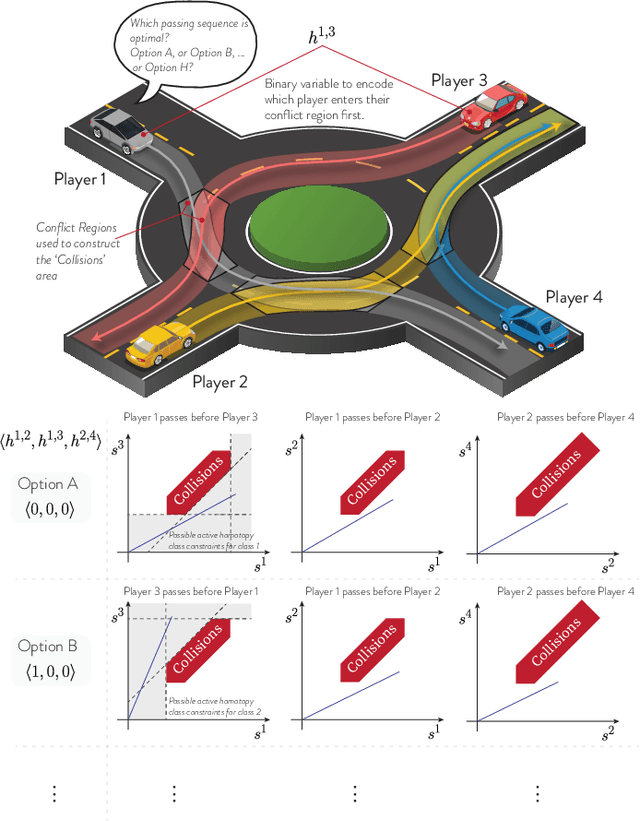
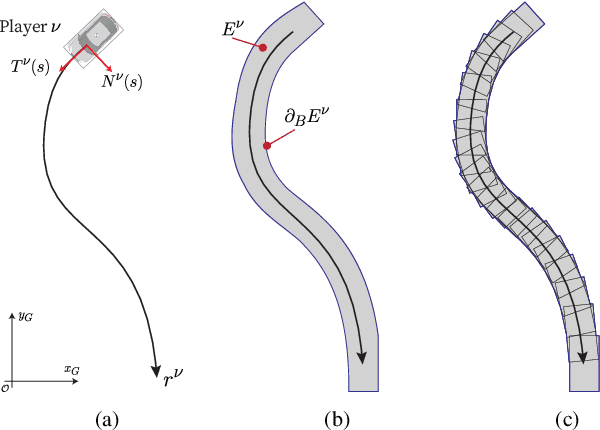
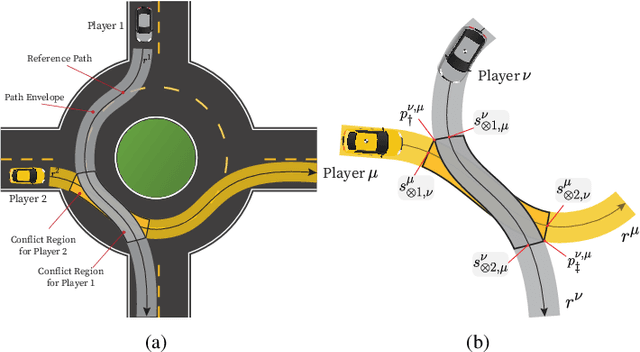
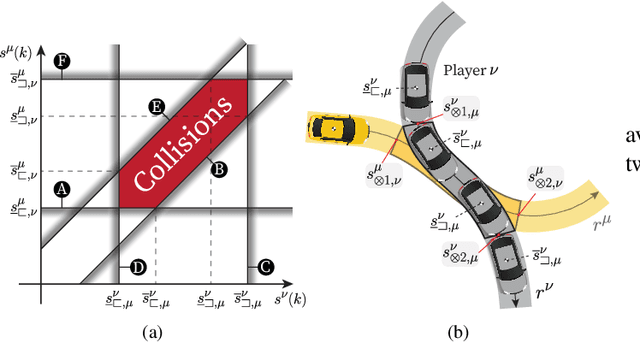
We propose a tactical homotopy-aware decision-making framework for game-theoretic motion planning in urban environments. We model urban driving as a generalized Nash equilibrium problem and employ a mixed-integer approach to tame the combinatorial aspect of motion planning. More specifically, by utilizing homotopy classes, we partition the high-dimensional solution space into finite, well-defined subregions. Each subregion (homotopy) corresponds to a high-level tactical decision, such as the passing order between pairs of players. The proposed formulation allows to find global optimal Nash equilibria in a computationally tractable manner by solving a mixed-integer quadratic program. Each homotopy decision is represented by a binary variable that activates different sets of linear collision avoidance constraints. This extra homotopic constraint allows to find solutions in a more efficient way (on a roundabout scenario on average 5-times faster). We experimentally validate the proposed approach on scenarios taken from the rounD dataset. Simulation-based testing in receding horizon fashion demonstrates the capability of the framework in achieving globally optimal solutions while yielding a 78% average decrease in the computational time with respect to an implementation without the homotopic constraints.

A Counterfactual Safety Margin Perspective on the Scoring of Autonomous Vehicles' Riskiness

Autonomous Vehicles (AVs) have the potential to provide numerous societal benefits, such as decreased road accidents and increased overall transportation efficiency. However, quantifying the risk associated with AVs is challenging due to the lack of historical data and the rapidly evolving technology. This paper presents a data-driven framework for comparing the risk of different AVs' behaviors in various operational design domains (ODDs), based on counterfactual simulations of "misbehaving" road users. We introduce the concept of counterfactual safety margin, which represents the minimum deviation from normal behavior that could lead to a collision. This concept helps to find the most critical scenarios but also to assess the frequency and severity of risk of AVs. We show that the proposed methodology is applicable even when the AV's behavioral policy is unknown -- through worst- and best-case analyses -- making the method useful also to external third-party risk assessors. Our experimental results demonstrate the correlation between the safety margin, the driving policy quality, and the ODD shedding light on the relative risk associated with different AV providers. This work contributes to AV safety assessment and aids in addressing legislative and insurance concerns surrounding this emerging technology.

Factorization of Multi-Agent Sampling-Based Motion Planning

Modern robotics often involves multiple embodied agents operating within a shared environment. Path planning in these cases is considerably more challenging than in single-agent scenarios. Although standard Sampling-based Algorithms (SBAs) can be used to search for solutions in the robots' joint space, this approach quickly becomes computationally intractable as the number of agents increases. To address this issue, we integrate the concept of factorization into sampling-based algorithms, which requires only minimal modifications to existing methods. During the search for a solution we can decouple (i.e., factorize) different subsets of agents into independent lower-dimensional search spaces once we certify that their future solutions will be independent of each other using a factorization heuristic. Consequently, we progressively construct a lean hypergraph where certain (hyper-)edges split the agents to independent subgraphs. In the best case, this approach can reduce the growth in dimensionality of the search space from exponential to linear in the number of agents. On average, fewer samples are needed to find high-quality solutions while preserving the optimality, completeness, and anytime properties of SBAs. We present a general implementation of a factorized SBA, derive an analytical gain in terms of sample complexity for PRM*, and showcase empirical results for RRG.

How Bad is Selfish Driving? Bounding the Inefficiency of Equilibria in Urban Driving Games

We consider the interaction among agents engaging in a driving task and we model it as general-sum game. This class of games exhibits a plurality of different equilibria posing the issue of equilibrium selection. While selecting the most efficient equilibrium (in term of social cost) is often impractical from a computational standpoint, in this work we study the (in)efficiency of any equilibrium players might agree to play. More specifically, we bound the equilibrium inefficiency by modeling driving games as particular type of congestion games over spatio-temporal resources. We obtain novel guarantees that refine existing bounds on the Price of Anarchy (PoA) as a function of problem-dependent game parameters. For instance, the relative trade-off between proximity costs and personal objectives such as comfort and progress. Although the obtained guarantees concern open-loop trajectories, we observe efficient equilibria even when agents employ closed-loop policies trained via decentralized multi-agent reinforcement learning.

Posetal Games: Efficiency, Existence, and Refinement of Equilibria in Games with Prioritized Metrics

Modern applications require robots to comply with multiple, often conflicting rules and to interact with the other agents. We present Posetal Games as a class of games in which each player expresses a preference over the outcomes via a partially ordered set of metrics. This allows one to combine hierarchical priorities of each player with the interactive nature of the environment. By contextualizing standard game theoretical notions, we provide two sufficient conditions on the preference of the players to prove existence of pure Nash Equilibria in finite action sets. Moreover, we define formal operations on the preference structures and link them to a refinement of the game solutions, showing how the set of equilibria can be systematically shrunk. The presented results are showcased in a driving game where autonomous vehicles select from a finite set of trajectories. The results demonstrate the interpretability of results in terms of minimum-rank-violation for each player.