A Classification of Feedback Loops and Their Relation to Biases in Automated Decision-Making Systems

Prediction-based decision-making systems are becoming increasingly prevalent in various domains. Previous studies have demonstrated that such systems are vulnerable to runaway feedback loops, e.g., when police are repeatedly sent back to the same neighborhoods regardless of the actual rate of criminal activity, which exacerbate existing biases. In practice, the automated decisions have dynamic feedback effects on the system itself that can perpetuate over time, making it difficult for short-sighted design choices to control the system's evolution. While researchers started proposing longer-term solutions to prevent adverse outcomes (such as bias towards certain groups), these interventions largely depend on ad hoc modeling assumptions and a rigorous theoretical understanding of the feedback dynamics in ML-based decision-making systems is currently missing. In this paper, we use the language of dynamical systems theory, a branch of applied mathematics that deals with the analysis of the interconnection of systems with dynamic behaviors, to rigorously classify the different types of feedback loops in the ML-based decision-making pipeline. By reviewing existing scholarly work, we show that this classification covers many examples discussed in the algorithmic fairness community, thereby providing a unifying and principled framework to study feedback loops. By qualitative analysis, and through a simulation example of recommender systems, we show which specific types of ML biases are affected by each type of feedback loop. We find that the existence of feedback loops in the ML-based decision-making pipeline can perpetuate, reinforce, or even reduce ML biases.

Enforcing Group Fairness in Algorithmic Decision Making: Utility Maximization Under Sufficiency

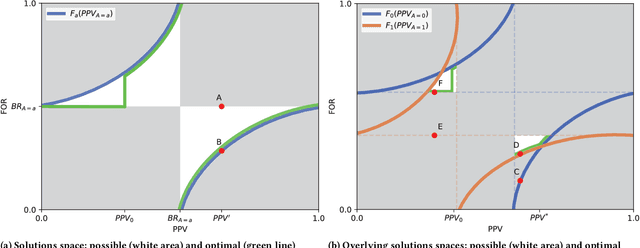
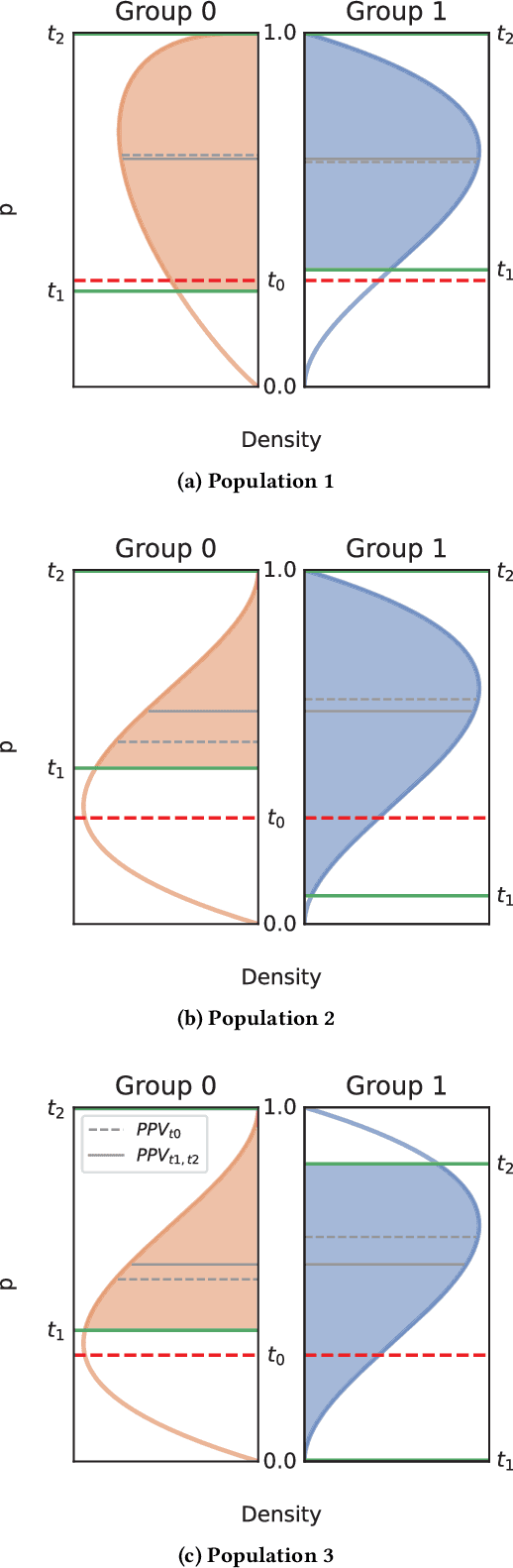
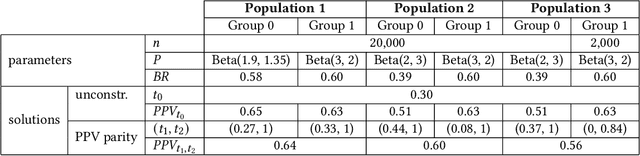
Binary decision making classifiers are not fair by default. Fairness requirements are an additional element to the decision making rationale, which is typically driven by maximizing some utility function. In that sense, algorithmic fairness can be formulated as a constrained optimization problem. This paper contributes to the discussion on how to implement fairness, focusing on the fairness concepts of positive predictive value (PPV) parity, false omission rate (FOR) parity, and sufficiency (which combines the former two). We show that group-specific threshold rules are optimal for PPV parity and FOR parity, similar to well-known results for other group fairness criteria. However, depending on the underlying population distributions and the utility function, we find that sometimes an upper-bound threshold rule for one group is optimal: utility maximization under PPV parity (or FOR parity) might thus lead to selecting the individuals with the smallest utility for one group, instead of selecting the most promising individuals. This result is counter-intuitive and in contrast to the analogous solutions for statistical parity and equality of opportunity. We also provide a solution for the optimal decision rules satisfying the fairness constraint sufficiency. We show that more complex decision rules are required and that this leads to within-group unfairness for all but one of the groups. We illustrate our findings based on simulated and real data.

Incentives in Two-sided Matching Markets with Prediction-enhanced Preference-formation

Two-sided matching markets have long existed to pair agents in the absence of regulated exchanges. A common example is school choice, where a matching mechanism uses student and school preferences to assign students to schools. In such settings, forming preferences is both difficult and critical. Prior work has suggested various prediction mechanisms that help agents make decisions about their preferences. Although often deployed together, these matching and prediction mechanisms are almost always analyzed separately. The present work shows that at the intersection of the two lies a previously unexplored type of strategic behavior: agents returning to the market (e.g., schools) can attack future predictions by interacting short-term non-optimally with their matches. Here, we first introduce this type of strategic behavior, which we call an `adversarial interaction attack'. Next, we construct a formal economic model that captures the feedback loop between prediction mechanisms designed to assist agents and the matching mechanism used to pair them. This economic model allows us to analyze adversarial interaction attacks. Finally, using school choice as an example, we build a simulation to show that, as the trust in and accuracy of predictions increases, schools gain progressively more by initiating an adversarial interaction attack. We also show that this attack increases inequality in the student population.