On Prediction-Modelers and Decision-Makers: Why Fairness Requires More Than a Fair Prediction Model

An implicit ambiguity in the field of prediction-based decision-making regards the relation between the concepts of prediction and decision. Much of the literature in the field tends to blur the boundaries between the two concepts and often simply speaks of 'fair prediction.' In this paper, we point out that a differentiation of these concepts is helpful when implementing algorithmic fairness. Even if fairness properties are related to the features of the used prediction model, what is more properly called 'fair' or 'unfair' is a decision system, not a prediction model. This is because fairness is about the consequences on human lives, created by a decision, not by a prediction. We clarify the distinction between the concepts of prediction and decision and show the different ways in which these two elements influence the final fairness properties of a prediction-based decision system. In addition to exploring this relationship conceptually and practically, we propose a framework that enables a better understanding and reasoning of the conceptual logic of creating fairness in prediction-based decision-making. In our framework, we specify different roles, namely the 'prediction-modeler' and the 'decision-maker,' and the information required from each of them for being able to implement fairness of the system. Our framework allows for deriving distinct responsibilities for both roles and discussing some insights related to ethical and legal requirements. Our contribution is twofold. First, we shift the focus from abstract algorithmic fairness to context-dependent decision-making, recognizing diverse actors with unique objectives and independent actions. Second, we provide a conceptual framework that can help structure prediction-based decision problems with respect to fairness issues, identify responsibilities, and implement fairness governance mechanisms in real-world scenarios.

Group Fairness in Prediction-Based Decision Making: From Moral Assessment to Implementation

Ensuring fairness of prediction-based decision making is based on statistical group fairness criteria. Which one of these criteria is the morally most appropriate one depends on the context, and its choice requires an ethical analysis. In this paper, we present a step-by-step procedure integrating three elements: (a) a framework for the moral assessment of what fairness means in a given context, based on the recently proposed general principle of "Fair equality of chances" (FEC) (b) a mapping of the assessment's results to established statistical group fairness criteria, and (c) a method for integrating the thus-defined fairness into optimal decision making. As a second contribution, we show new applications of the FEC principle and show that, with this extension, the FEC framework covers all types of group fairness criteria: independence, separation, and sufficiency. Third, we introduce an extended version of the FEC principle, which additionally allows accounting for morally irrelevant elements of the fairness assessment and links to well-known relaxations of the fairness criteria. This paper presents a framework to develop fair decision systems in a conceptually sound way, combining the moral and the computational elements of fair prediction-based decision-making in an integrated approach. Data and code to reproduce our results are available at https://github.com/joebaumann/fair-prediction-based-decision-making.

Distributive Justice as the Foundational Premise of Fair ML: Unification, Extension, and Interpretation of Group Fairness Metrics

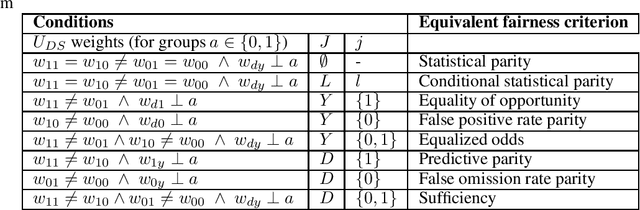
Group fairness metrics are an established way of assessing the fairness of prediction-based decision-making systems. However, these metrics are still insufficiently linked to philosophical theories, and their moral meaning is often unclear. We propose a general framework for analyzing the fairness of decision systems based on theories of distributive justice, encompassing different established ``patterns of justice'' that correspond to different normative positions. We show that the most popular group fairness metrics can be interpreted as special cases of our approach. Thus, we provide a unifying and interpretative framework for group fairness metrics that reveals the normative choices associated with each of them and that allows understanding their moral substance. At the same time, we provide an extension of the space of possible fairness metrics beyond the ones currently discussed in the fair ML literature. Our framework also allows overcoming several limitations of group fairness metrics that have been criticized in the literature, most notably (1) that they are parity-based, i.e., that they demand some form of equality between groups, which may sometimes be harmful to marginalized groups, (2) that they only compare decisions across groups, but not the resulting consequences for these groups, and (3) that the full breadth of the distributive justice literature is not sufficiently represented.

A Justice-Based Framework for the Analysis of Algorithmic Fairness-Utility Trade-Offs

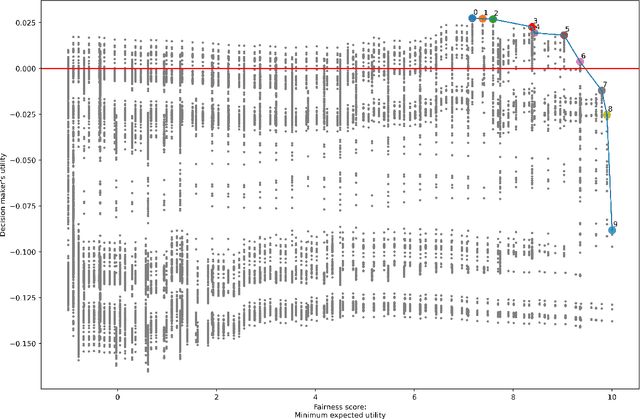
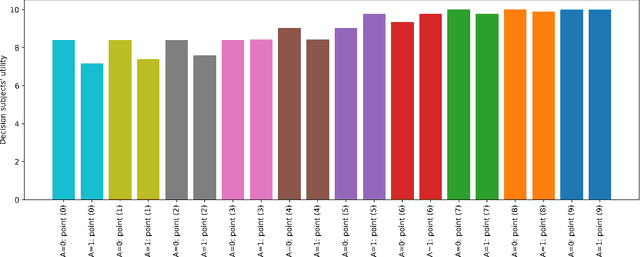
In prediction-based decision-making systems, different perspectives can be at odds: The short-term business goals of the decision makers are often in conflict with the decision subjects' wish to be treated fairly. Balancing these two perspectives is a question of values. We provide a framework to make these value-laden choices clearly visible. For this, we assume that we are given a trained model and want to find decision rules that balance the perspective of the decision maker and of the decision subjects. We provide an approach to formalize both perspectives, i.e., to assess the utility of the decision maker and the fairness towards the decision subjects. In both cases, the idea is to elicit values from decision makers and decision subjects that are then turned into something measurable. For the fairness evaluation, we build on the literature on welfare-based fairness and ask what a fair distribution of utility (or welfare) looks like. In this step, we build on well-known theories of distributive justice. This allows us to derive a fairness score that we then compare to the decision maker's utility for many different decision rules. This way, we provide an approach for balancing the utility of the decision maker and the fairness towards the decision subjects for a prediction-based decision-making system.

Enforcing Group Fairness in Algorithmic Decision Making: Utility Maximization Under Sufficiency

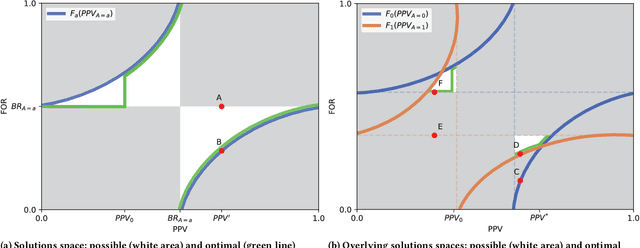
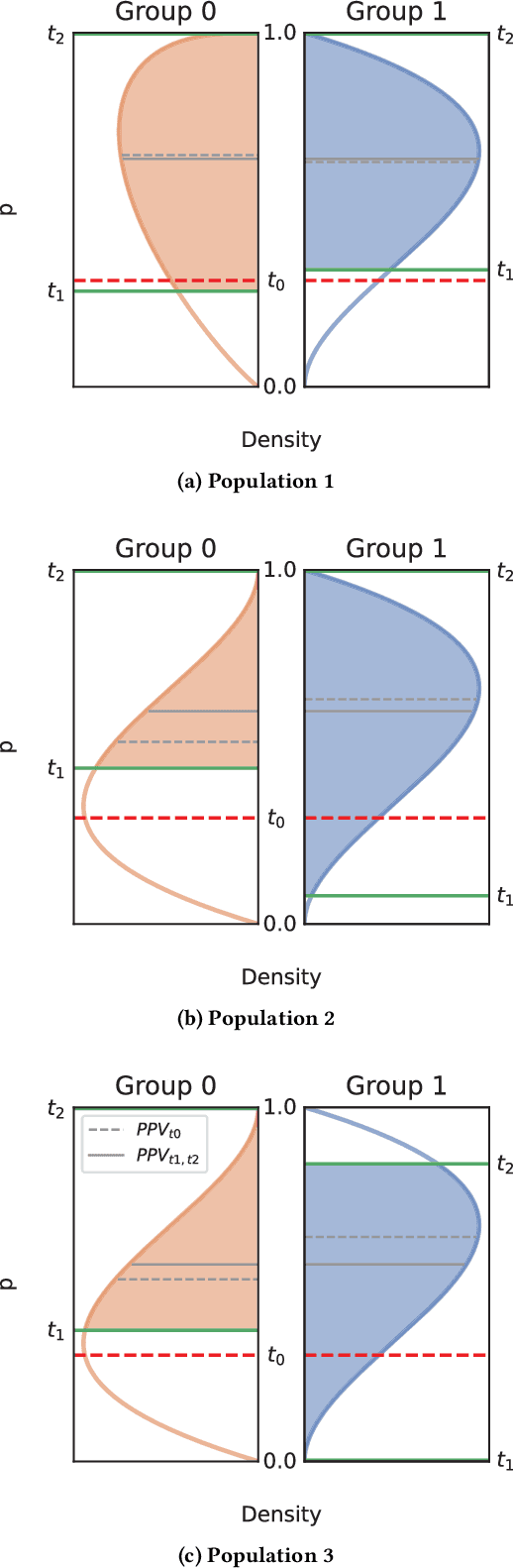
Binary decision making classifiers are not fair by default. Fairness requirements are an additional element to the decision making rationale, which is typically driven by maximizing some utility function. In that sense, algorithmic fairness can be formulated as a constrained optimization problem. This paper contributes to the discussion on how to implement fairness, focusing on the fairness concepts of positive predictive value (PPV) parity, false omission rate (FOR) parity, and sufficiency (which combines the former two). We show that group-specific threshold rules are optimal for PPV parity and FOR parity, similar to well-known results for other group fairness criteria. However, depending on the underlying population distributions and the utility function, we find that sometimes an upper-bound threshold rule for one group is optimal: utility maximization under PPV parity (or FOR parity) might thus lead to selecting the individuals with the smallest utility for one group, instead of selecting the most promising individuals. This result is counter-intuitive and in contrast to the analogous solutions for statistical parity and equality of opportunity. We also provide a solution for the optimal decision rules satisfying the fairness constraint sufficiency. We show that more complex decision rules are required and that this leads to within-group unfairness for all but one of the groups. We illustrate our findings based on simulated and real data.

Is calibration a fairness requirement? An argument from the point of view of moral philosophy and decision theory

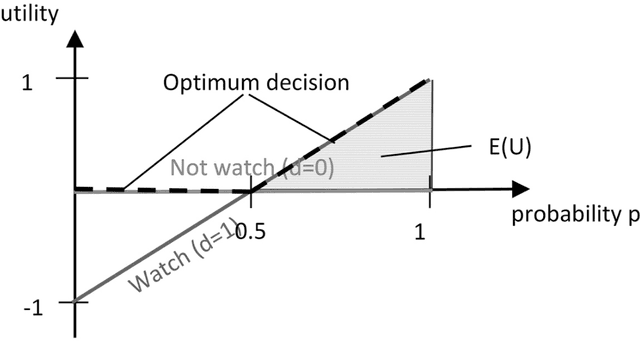
In this paper, we provide a moral analysis of two criteria of statistical fairness debated in the machine learning literature: 1) calibration between groups and 2) equality of false positive and false negative rates between groups. In our paper, we focus on moral arguments in support of either measure. The conflict between group calibration vs. false positive and false negative rate equality is one of the core issues in the debate about group fairness definitions among practitioners. For any thorough moral analysis, the meaning of the term fairness has to be made explicit and defined properly. For our paper, we equate fairness with (non-)discrimination, which is a legitimate understanding in the discussion about group fairness. More specifically, we equate it with prima facie wrongful discrimination in the sense this is used in Prof. Lippert-Rasmussen's treatment of this definition. In this paper, we argue that a violation of group calibration may be unfair in some cases, but not unfair in others. This is in line with claims already advanced in the literature, that algorithmic fairness should be defined in a way that is sensitive to context. The most important practical implication is that arguments based on examples in which fairness requires between-group calibration, or equality in the false-positive/false-negative rates, do no generalize. For it may be that group calibration is a fairness requirement in one case, but not in another.

A Systematic Approach to Group Fairness in Automated Decision Making

While the field of algorithmic fairness has brought forth many ways to measure and improve the fairness of machine learning models, these findings are still not widely used in practice. We suspect that one reason for this is that the field of algorithmic fairness came up with a lot of definitions of fairness, which are difficult to navigate. The goal of this paper is to provide data scientists with an accessible introduction to group fairness metrics and to give some insight into the philosophical reasoning for caring about these metrics. We will do this by considering in which sense socio-demographic groups are compared for making a statement on fairness.

On the Moral Justification of Statistical Parity

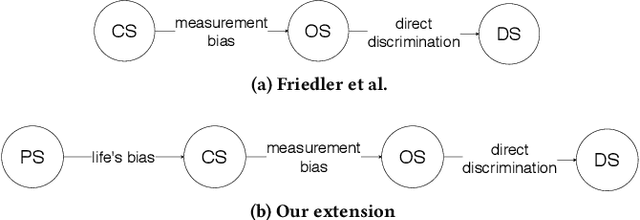
A crucial but often neglected aspect of algorithmic fairness is the question of how we justify enforcing a certain fairness metric from a moral perspective. When fairness metrics are defined, they are typically argued for by highlighting their mathematical properties. Rarely are the moral assumptions beneath the metric explained. Our aim in this paper is to consider the moral aspects associated with the statistical fairness criterion of independence (statistical parity). To this end, we consider previous work, which discusses the two worldviews "What You See Is What You Get" (WYSIWYG) and "We're All Equal" (WAE) and by doing so provides some guidance for clarifying the possible assumptions in the design of algorithms. We present an extension of this work, which centers on morality. The most natural moral extension is that independence needs to be fulfilled if and only if differences in predictive features (e.g., ability to perform well on a job, propensity to commit a crime, etc.) between socio-demographic groups are caused by unjust social disparities and measurement errors. Through two counterexamples, we demonstrate that this extension is not universally true. This means that the question of whether independence should be used or not cannot be satisfactorily answered by only considering the justness of differences in the predictive features.