Nicolas Pelzmann
Stability and Robustness of Distributed Suboptimal Model Predictive Control
Nov 14, 2022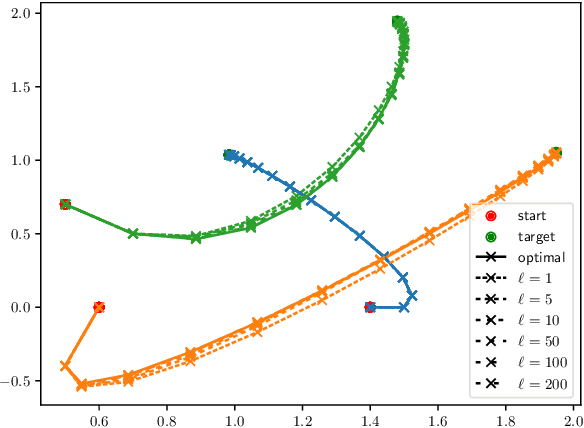
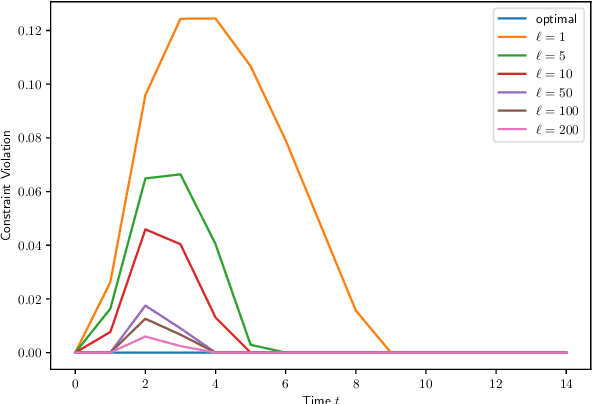
Abstract:In distributed model predictive control (MPC), the control input at each sampling time is computed by solving a large-scale optimal control problem (OCP) over a finite horizon using distributed algorithms. Typically, such algorithms require several (virtually, infinite) communication rounds between the subsystems to converge, which is a major drawback both computationally and from an energetic perspective (for wireless systems). Motivated by these challenges, we propose a suboptimal distributed MPC scheme in which the total communication burden is distributed also in time, by maintaining a running solution estimate for the large-scale OCP and updating it at each sampling time. We demonstrate that, under some regularity conditions, the resulting suboptimal MPC control law recovers the qualitative robust stability properties of optimal MPC, if the communication budget at each sampling time is large enough.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge