Maximum likelihood inference for high-dimensional problems with multiaffine variable relations

Maximum Likelihood Estimation of continuous variable models can be very challenging in high dimensions, due to potentially complex probability distributions. The existence of multiple interdependencies among variables can make it very difficult to establish convergence guarantees. This leads to a wide use of brute-force methods, such as grid searching and Monte-Carlo sampling and, when applicable, complex and problem-specific algorithms. In this paper, we consider inference problems where the variables are related by multiaffine expressions. We propose a novel Alternating and Iteratively-Reweighted Least Squares (AIRLS) algorithm, and prove its convergence for problems with Generalized Normal Distributions. We also provide an efficient method to compute the variance of the estimates obtained using AIRLS. Finally, we show how the method can be applied to graphical statistical models. We perform numerical experiments on several inference problems, showing significantly better performance than state-of-the-art approaches in terms of scalability, robustness to noise, and convergence speed due to an empirically observed super-linear convergence rate.

Robust online joint state/input/parameter estimation of linear systems

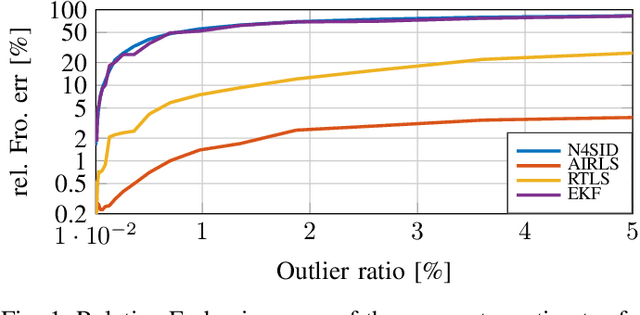
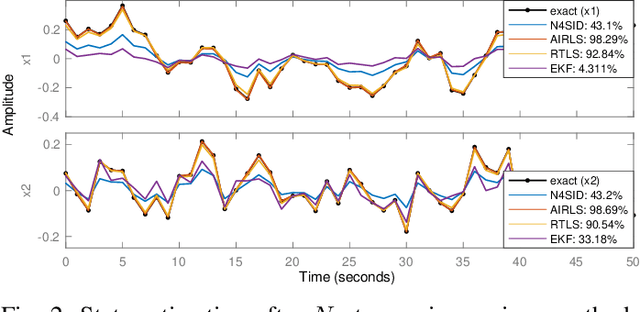
This paper presents a method for jointly estimating the state, input, and parameters of linear systems in an online fashion. The method is specially designed for measurements that are corrupted with non-Gaussian noise or outliers, which are commonly found in engineering applications. In particular, it combines recursive, alternating, and iteratively-reweighted least squares into a single, one-step algorithm, which solves the estimation problem online and benefits from the robustness of least-deviation regression methods. The convergence of the iterative method is formally guaranteed. Numerical experiments show the good performance of the estimation algorithm in presence of outliers and in comparison to state-of-the-art methods.

Bayesian Error-in-Variables Models for the Identification of Power Networks

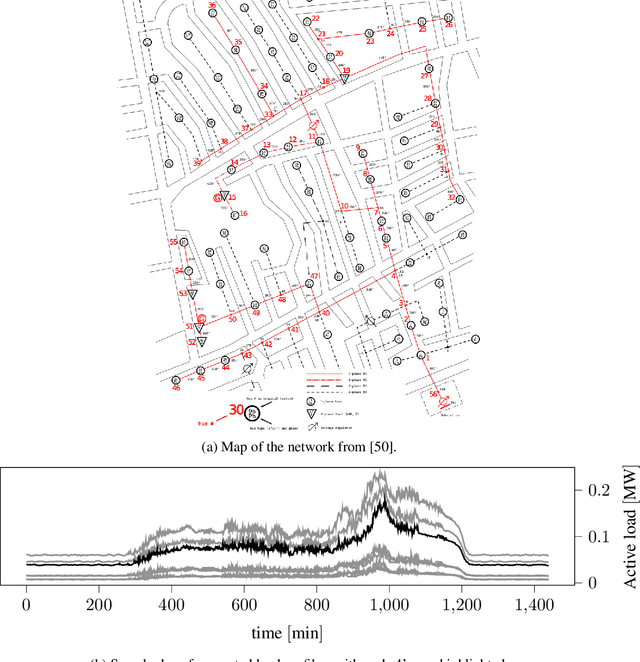
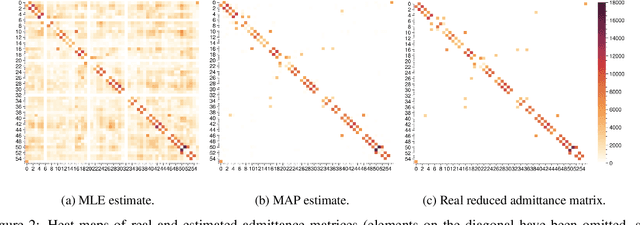
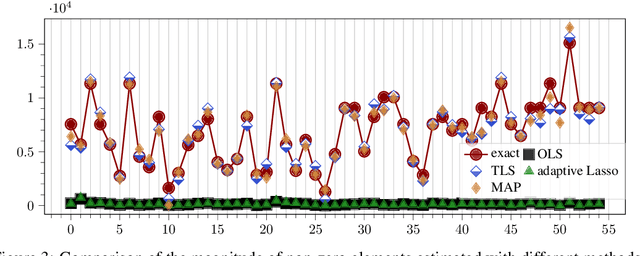
The increasing integration of intermittent renewable generation, especially at the distribution level,necessitates advanced planning and optimisation methodologies contingent on the knowledge of thegrid, specifically the admittance matrix capturing the topology and line parameters of an electricnetwork. However, a reliable estimate of the admittance matrix may either be missing or quicklybecome obsolete for temporally varying grids. In this work, we propose a data-driven identificationmethod utilising voltage and current measurements collected from micro-PMUs. More precisely,we first present a maximum likelihood approach and then move towards a Bayesian framework,leveraging the principles of maximum a posteriori estimation. In contrast with most existing con-tributions, our approach not only factors in measurement noise on both voltage and current data,but is also capable of exploiting available a priori information such as sparsity patterns and knownline parameters. Simulations conducted on benchmark cases demonstrate that, compared to otheralgorithms, our method can achieve significantly greater accuracy.