NeoRL: Efficient Exploration for Nonepisodic RL

We study the problem of nonepisodic reinforcement learning (RL) for nonlinear dynamical systems, where the system dynamics are unknown and the RL agent has to learn from a single trajectory, i.e., without resets. We propose Nonepisodic Optimistic RL (NeoRL), an approach based on the principle of optimism in the face of uncertainty. NeoRL uses well-calibrated probabilistic models and plans optimistically w.r.t. the epistemic uncertainty about the unknown dynamics. Under continuity and bounded energy assumptions on the system, we provide a first-of-its-kind regret bound of $\setO(\beta_T \sqrt{T \Gamma_T})$ for general nonlinear systems with Gaussian process dynamics. We compare NeoRL to other baselines on several deep RL environments and empirically demonstrate that NeoRL achieves the optimal average cost while incurring the least regret.

When to Sense and Control? A Time-adaptive Approach for Continuous-Time RL

Reinforcement learning (RL) excels in optimizing policies for discrete-time Markov decision processes (MDP). However, various systems are inherently continuous in time, making discrete-time MDPs an inexact modeling choice. In many applications, such as greenhouse control or medical treatments, each interaction (measurement or switching of action) involves manual intervention and thus is inherently costly. Therefore, we generally prefer a time-adaptive approach with fewer interactions with the system. In this work, we formalize an RL framework, Time-adaptive Control & Sensing (TaCoS), that tackles this challenge by optimizing over policies that besides control predict the duration of its application. Our formulation results in an extended MDP that any standard RL algorithm can solve. We demonstrate that state-of-the-art RL algorithms trained on TaCoS drastically reduce the interaction amount over their discrete-time counterpart while retaining the same or improved performance, and exhibiting robustness over discretization frequency. Finally, we propose OTaCoS, an efficient model-based algorithm for our setting. We show that OTaCoS enjoys sublinear regret for systems with sufficiently smooth dynamics and empirically results in further sample-efficiency gains.

Bridging the Sim-to-Real Gap with Bayesian Inference

We present SIM-FSVGD for learning robot dynamics from data. As opposed to traditional methods, SIM-FSVGD leverages low-fidelity physical priors, e.g., in the form of simulators, to regularize the training of neural network models. While learning accurate dynamics already in the low data regime, SIM-FSVGD scales and excels also when more data is available. We empirically show that learning with implicit physical priors results in accurate mean model estimation as well as precise uncertainty quantification. We demonstrate the effectiveness of SIM-FSVGD in bridging the sim-to-real gap on a high-performance RC racecar system. Using model-based RL, we demonstrate a highly dynamic parking maneuver with drifting, using less than half the data compared to the state of the art.

Information-based Transductive Active Learning

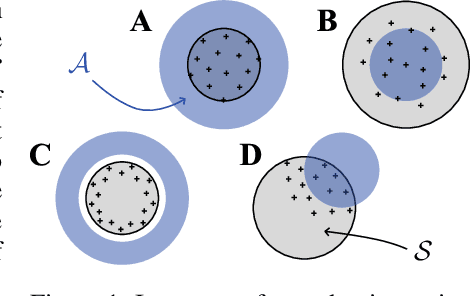
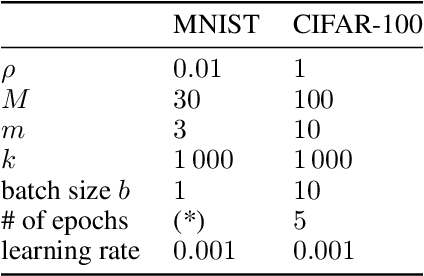
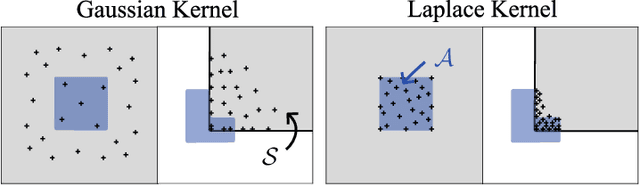
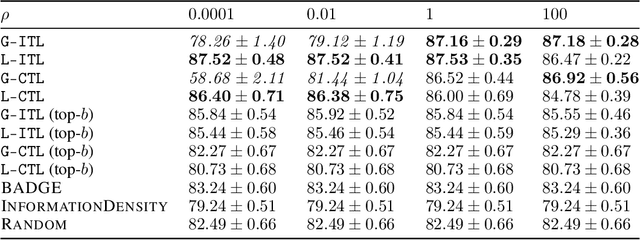
We generalize active learning to address real-world settings where sampling is restricted to an accessible region of the domain, while prediction targets may lie outside this region. To this end, we propose ITL, short for information-based transductive learning, an approach which samples adaptively to maximize the information gained about specified prediction targets. We show, under general regularity assumptions, that ITL converges uniformly to the smallest possible uncertainty obtainable from the accessible data. We demonstrate ITL in two key applications: Few-shot fine-tuning of large neural networks and safe Bayesian optimization, and in both cases, ITL significantly outperforms the state-of-the-art.

Active Few-Shot Fine-Tuning

We study the active few-shot fine-tuning of large neural networks to downstream tasks. We show that few-shot fine-tuning is an instance of a generalization of classical active learning, transductive active learning, and we propose ITL, short for information-based transductive learning, an approach which samples adaptively to maximize the information gained about specified downstream tasks. Under general regularity assumptions, we prove that ITL converges uniformly to the smallest possible uncertainty obtainable from the accessible data. To the best of our knowledge, we are the first to derive generalization bounds of this kind, and they may be of independent interest for active learning. We apply ITL to the few-shot fine-tuning of large neural networks and show that ITL substantially improves upon the state-of-the-art.

Efficient Exploration in Continuous-time Model-based Reinforcement Learning

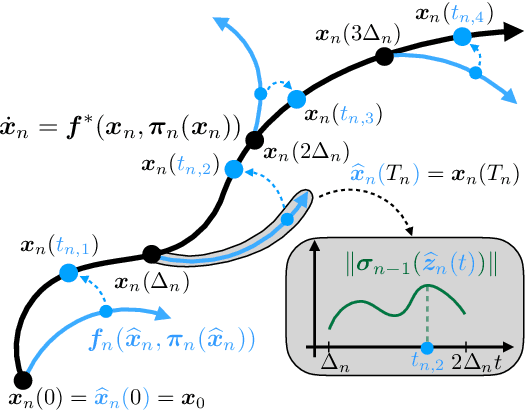
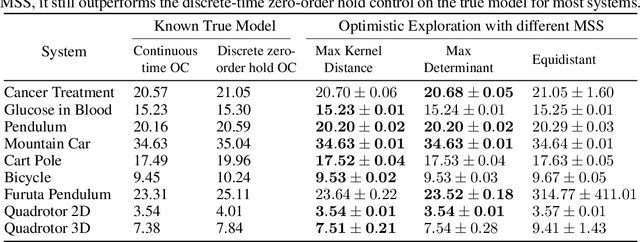
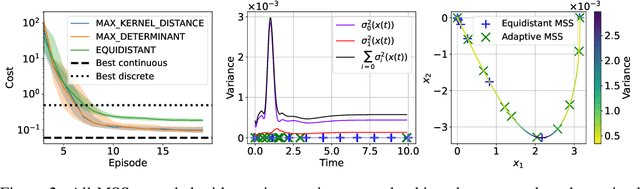
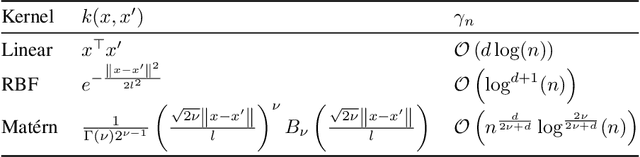
Reinforcement learning algorithms typically consider discrete-time dynamics, even though the underlying systems are often continuous in time. In this paper, we introduce a model-based reinforcement learning algorithm that represents continuous-time dynamics using nonlinear ordinary differential equations (ODEs). We capture epistemic uncertainty using well-calibrated probabilistic models, and use the optimistic principle for exploration. Our regret bounds surface the importance of the measurement selection strategy(MSS), since in continuous time we not only must decide how to explore, but also when to observe the underlying system. Our analysis demonstrates that the regret is sublinear when modeling ODEs with Gaussian Processes (GP) for common choices of MSS, such as equidistant sampling. Additionally, we propose an adaptive, data-dependent, practical MSS that, when combined with GP dynamics, also achieves sublinear regret with significantly fewer samples. We showcase the benefits of continuous-time modeling over its discrete-time counterpart, as well as our proposed adaptive MSS over standard baselines, on several applications.

Optimistic Active Exploration of Dynamical Systems

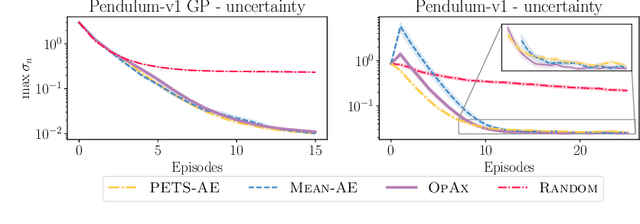
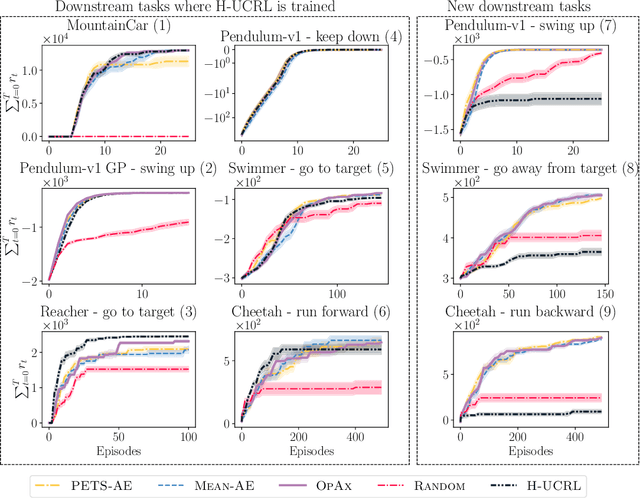
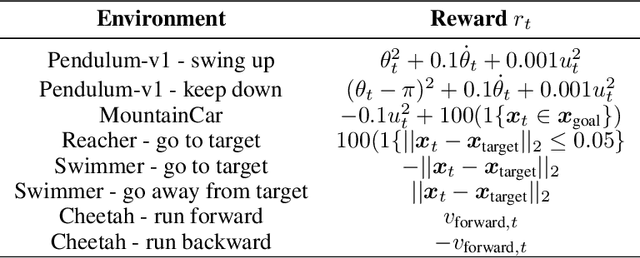
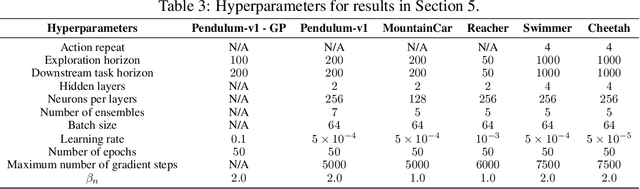
Reinforcement learning algorithms commonly seek to optimize policies for solving one particular task. How should we explore an unknown dynamical system such that the estimated model allows us to solve multiple downstream tasks in a zero-shot manner? In this paper, we address this challenge, by developing an algorithm -- OPAX -- for active exploration. OPAX uses well-calibrated probabilistic models to quantify the epistemic uncertainty about the unknown dynamics. It optimistically -- w.r.t. to plausible dynamics -- maximizes the information gain between the unknown dynamics and state observations. We show how the resulting optimization problem can be reduced to an optimal control problem that can be solved at each episode using standard approaches. We analyze our algorithm for general models, and, in the case of Gaussian process dynamics, we give a sample complexity bound and show that the epistemic uncertainty converges to zero. In our experiments, we compare OPAX with other heuristic active exploration approaches on several environments. Our experiments show that OPAX is not only theoretically sound but also performs well for zero-shot planning on novel downstream tasks.

Distributional Gradient Matching for Learning Uncertain Neural Dynamics Models

Differential equations in general and neural ODEs in particular are an essential technique in continuous-time system identification. While many deterministic learning algorithms have been designed based on numerical integration via the adjoint method, many downstream tasks such as active learning, exploration in reinforcement learning, robust control, or filtering require accurate estimates of predictive uncertainties. In this work, we propose a novel approach towards estimating epistemically uncertain neural ODEs, avoiding the numerical integration bottleneck. Instead of modeling uncertainty in the ODE parameters, we directly model uncertainties in the state space. Our algorithm - distributional gradient matching (DGM) - jointly trains a smoother and a dynamics model and matches their gradients via minimizing a Wasserstein loss. Our experiments show that, compared to traditional approximate inference methods based on numerical integration, our approach is faster to train, faster at predicting previously unseen trajectories, and in the context of neural ODEs, significantly more accurate.

Iterative Correction of Sensor Degradation and a Bayesian Multi-Sensor Data Fusion Method

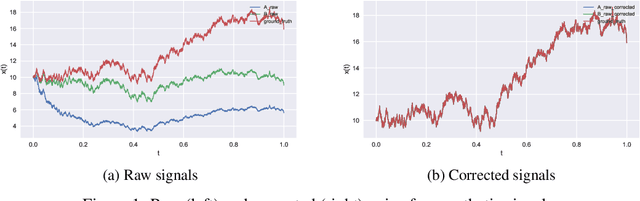
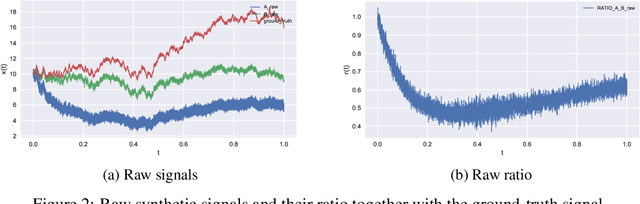
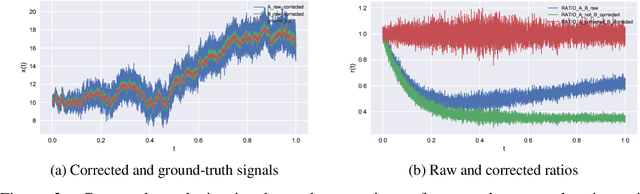
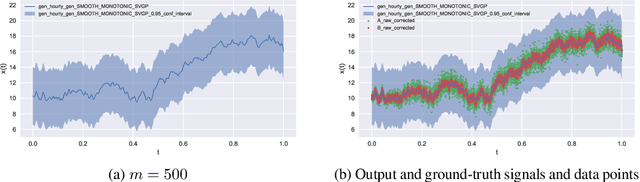
We present a novel method for inferring ground-truth signal from multiple degraded signals, affected by different amounts of sensor exposure. The algorithm learns a multiplicative degradation effect by performing iterative corrections of two signals solely from the ratio between them. The degradation function d should be continuous, satisfy monotonicity, and d(0) = 1. We use smoothed monotonic regression method, where we easily incorporate the aforementioned criteria to the fitting part. We include theoretical analysis and prove convergence to the ground-truth signal for the noiseless measurement model. Lastly, we present an approach to fuse the noisy corrected signals using Gaussian processes. We use sparse Gaussian processes that can be utilized for a large number of measurements together with a specialized kernel that enables the estimation of noise values of all sensors. The data fusion framework naturally handles data gaps and provides a simple and powerful method for observing the signal trends on multiple timescales(long-term and short-term signal properties). The viability of correction method is evaluated on a synthetic dataset with known ground-truth signal.

Learning Controllers for Unstable Linear Quadratic Regulators from a Single Trajectory

We present the first approach for learning -- from a single trajectory -- a linear quadratic regulator (LQR), even for unstable systems, without knowledge of the system dynamics and without requiring an initial stabilizing controller. Our central contribution is an efficient algorithm -- \emph{eXploration} -- that quickly identifies a stabilizing controller. Our approach utilizes robust System Level Synthesis (SLS), and we prove that it succeeds in a constant number of iterations. Our approach can be used to initialize existing algorithms that require a stabilizing controller as input. When used in this way, it yields a method for learning LQRs from a single trajectory and even for unstable systems, while suffering at most $\widetilde{\mathcal{O}}(\sqrt{T})$ regret.