Information-based Transductive Active Learning

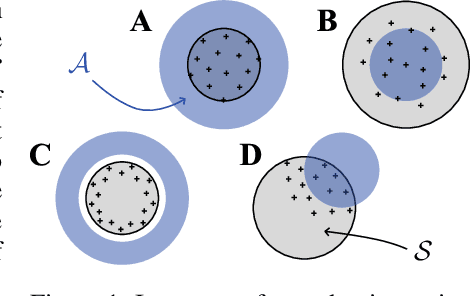
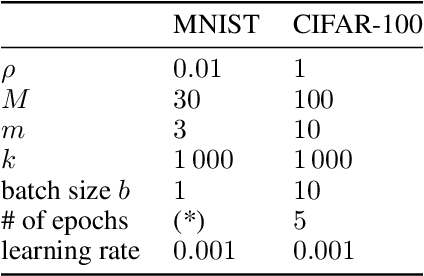
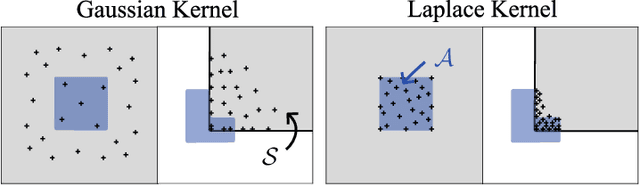
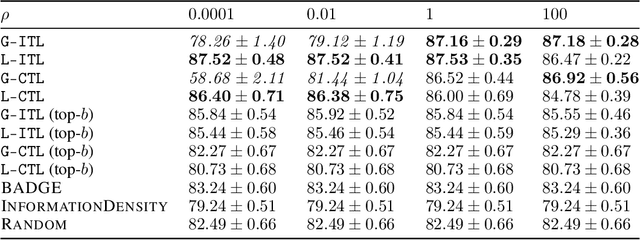
We generalize active learning to address real-world settings where sampling is restricted to an accessible region of the domain, while prediction targets may lie outside this region. To this end, we propose ITL, short for information-based transductive learning, an approach which samples adaptively to maximize the information gained about specified prediction targets. We show, under general regularity assumptions, that ITL converges uniformly to the smallest possible uncertainty obtainable from the accessible data. We demonstrate ITL in two key applications: Few-shot fine-tuning of large neural networks and safe Bayesian optimization, and in both cases, ITL significantly outperforms the state-of-the-art.