Learning Stable Deep Dynamics Models for Partially Observed or Delayed Dynamical Systems

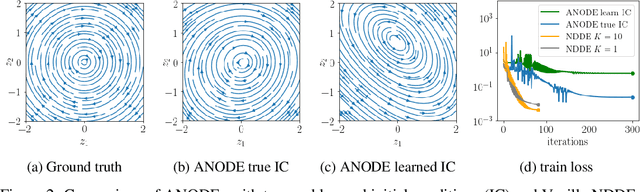
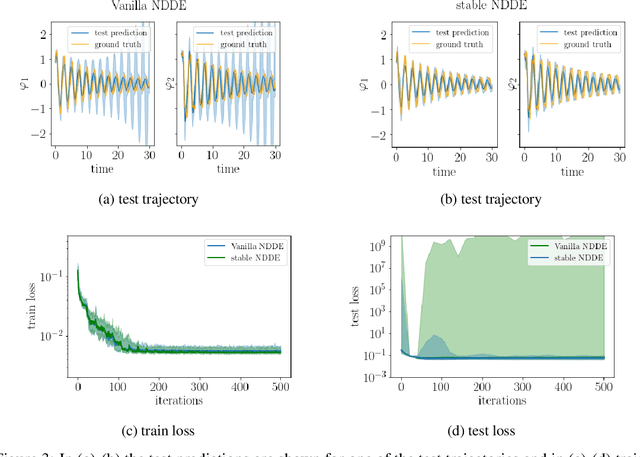
Learning how complex dynamical systems evolve over time is a key challenge in system identification. For safety critical systems, it is often crucial that the learned model is guaranteed to converge to some equilibrium point. To this end, neural ODEs regularized with neural Lyapunov functions are a promising approach when states are fully observed. For practical applications however, partial observations are the norm. As we will demonstrate, initialization of unobserved augmented states can become a key problem for neural ODEs. To alleviate this issue, we propose to augment the system's state with its history. Inspired by state augmentation in discrete-time systems, we thus obtain neural delay differential equations. Based on classical time delay stability analysis, we then show how to ensure stability of the learned models, and theoretically analyze our approach. Our experiments demonstrate its applicability to stable system identification of partially observed systems and learning a stabilizing feedback policy in delayed feedback control.

Distributional Gradient Matching for Learning Uncertain Neural Dynamics Models

Differential equations in general and neural ODEs in particular are an essential technique in continuous-time system identification. While many deterministic learning algorithms have been designed based on numerical integration via the adjoint method, many downstream tasks such as active learning, exploration in reinforcement learning, robust control, or filtering require accurate estimates of predictive uncertainties. In this work, we propose a novel approach towards estimating epistemically uncertain neural ODEs, avoiding the numerical integration bottleneck. Instead of modeling uncertainty in the ODE parameters, we directly model uncertainties in the state space. Our algorithm - distributional gradient matching (DGM) - jointly trains a smoother and a dynamics model and matches their gradients via minimizing a Wasserstein loss. Our experiments show that, compared to traditional approximate inference methods based on numerical integration, our approach is faster to train, faster at predicting previously unseen trajectories, and in the context of neural ODEs, significantly more accurate.

SLEIPNIR: Deterministic and Provably Accurate Feature Expansion for Gaussian Process Regression with Derivatives

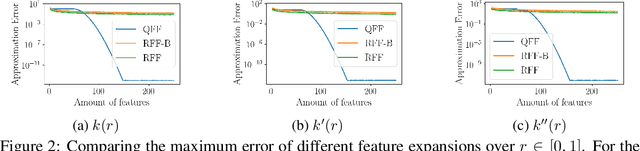
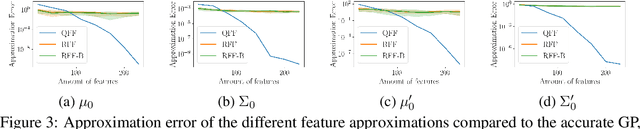
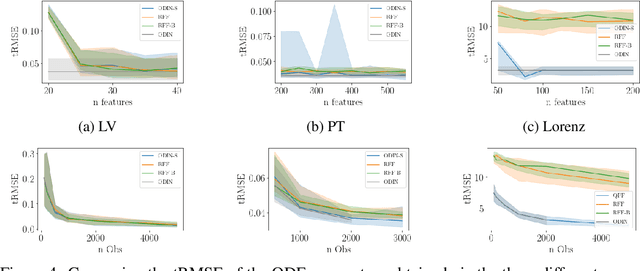
Gaussian processes are an important regression tool with excellent analytic properties which allow for direct integration of derivative observations. However, vanilla GP methods scale cubically in the amount of observations. In this work, we propose a novel approach for scaling GP regression with derivatives based on quadrature Fourier features. We then prove deterministic, non-asymptotic and exponentially fast decaying error bounds which apply for both the approximated kernel as well as the approximated posterior. To furthermore illustrate the practical applicability of our method, we then apply it to ODIN, a recently developed algorithm for ODE parameter inference. In an extensive experiments section, all results are empirically validated, demonstrating the speed, accuracy, and practical applicability of this approach.

AReS and MaRS - Adversarial and MMD-Minimizing Regression for SDEs

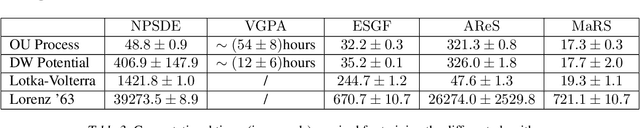
Stochastic differential equations are an important modeling class in many disciplines. Consequently, there exist many methods relying on various discretization and numerical integration schemes. In this paper, we propose a novel, probabilistic model for estimating the drift and diffusion given noisy observations of the underlying stochastic system. Using state-of-the-art adversarial and moment matching inference techniques, we circumvent the use of the discretization schemes as seen in classical approaches. This yields significant improvements in parameter estimation accuracy and robustness given random initial guesses. On four commonly used benchmark systems, we demonstrate the performance of our algorithms compared to state-of-the-art solutions based on extended Kalman filtering and Gaussian processes.

ODIN: ODE-Informed Regression for Parameter and State Inference in Time-Continuous Dynamical Systems

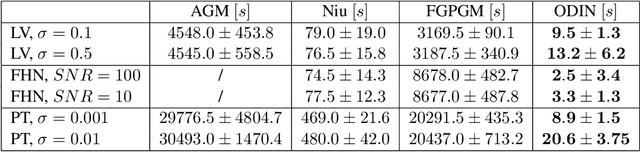
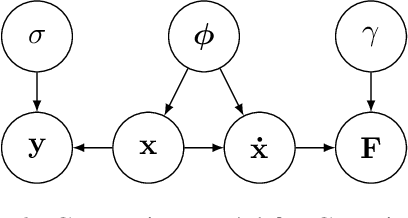
Parameter inference in ordinary differential equations is an important problem in many applied sciences and in engineering, especially in a data-scarce setting. In this work, we introduce a novel generative modeling approach based on constrained Gaussian processes and use it to create a computationally and data efficient algorithm for state and parameter inference. In an extensive set of experiments, our approach outperforms its competitors both in terms of accuracy and computational cost for parameter inference. It also shows promising results for the much more challenging problem of model selection.

Fast Gaussian Process Based Gradient Matching for Parameter Identification in Systems of Nonlinear ODEs

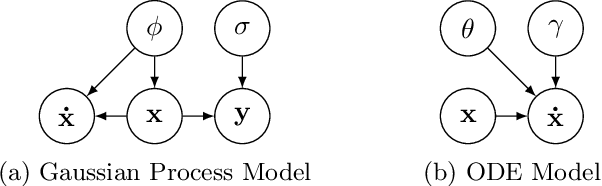
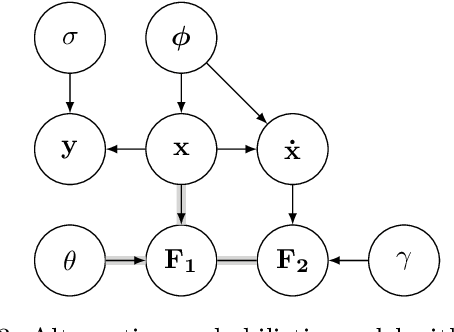
Parameter identification and comparison of dynamical systems is a challenging task in many fields. Bayesian approaches based on Gaussian process regression over time-series data have been successfully applied to infer the parameters of a dynamical system without explicitly solving it. While the benefits in computational cost are well established, a rigorous mathematical framework has been missing. We offer a novel interpretation which leads to a better understanding and improvements in state-of-the-art performance in terms of accuracy for nonlinear dynamical systems.