Fast Gaussian Process Based Gradient Matching for Parameter Identification in Systems of Nonlinear ODEs

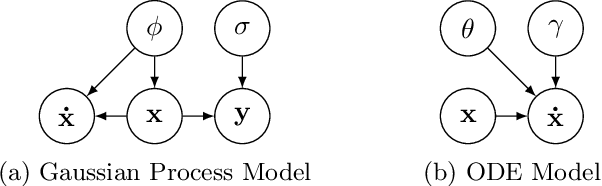
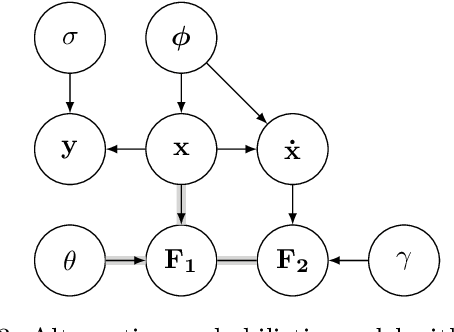
Parameter identification and comparison of dynamical systems is a challenging task in many fields. Bayesian approaches based on Gaussian process regression over time-series data have been successfully applied to infer the parameters of a dynamical system without explicitly solving it. While the benefits in computational cost are well established, a rigorous mathematical framework has been missing. We offer a novel interpretation which leads to a better understanding and improvements in state-of-the-art performance in terms of accuracy for nonlinear dynamical systems.

Model Selection for Gaussian Process Regression by Approximation Set Coding

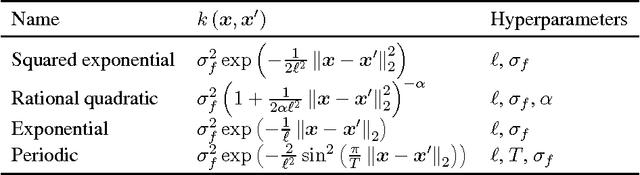
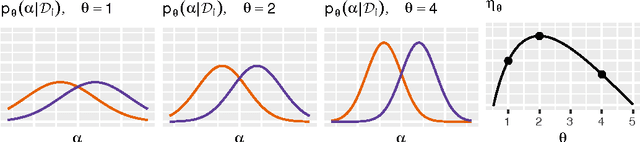
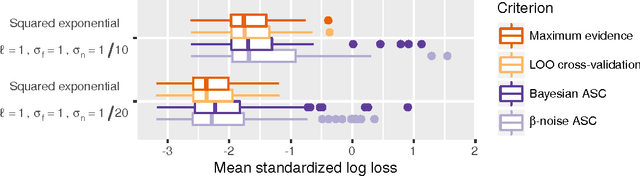
Gaussian processes are powerful, yet analytically tractable models for supervised learning. A Gaussian process is characterized by a mean function and a covariance function (kernel), which are determined by a model selection criterion. The functions to be compared do not just differ in their parametrization but in their fundamental structure. It is often not clear which function structure to choose, for instance to decide between a squared exponential and a rational quadratic kernel. Based on the principle of approximation set coding, we develop a framework for model selection to rank kernels for Gaussian process regression. In our experiments approximation set coding shows promise to become a model selection criterion competitive with maximum evidence (also called marginal likelihood) and leave-one-out cross-validation.