Paramater Optimization for Manipulator Motion Planning using a Novel Benchmark Set

Sampling-based motion planning algorithms have been continuously developed for more than two decades. Apart from mobile robots, they are also widely used in manipulator motion planning. Hence, these methods play a key role in collaborative and shared workspaces. Despite numerous improvements, their performance can highly vary depending on the chosen parameter setting. The optimal parameters depend on numerous factors such as the start state, the goal state and the complexity of the environment. Practitioners usually choose these values using their experience and tedious trial and error experiments. To address this problem, recent works combine hyperparameter optimization methods with motion planning. They show that tuning the planner's parameters can lead to shorter planning times and lower costs. It is not clear, however, how well such approaches generalize to a diverse set of planning problems that include narrow passages as well as barely cluttered environments. In this work, we analyze optimized planner settings for a large set of diverse planning problems. We then provide insights into the connection between the characteristics of the planning problem and the optimal parameters. As a result, we provide a list of recommended parameters for various use-cases. Our experiments are based on a novel motion planning benchmark for manipulators which we provide at https://mytuc.org/rybj.

Model Selection for Gaussian Process Regression by Approximation Set Coding

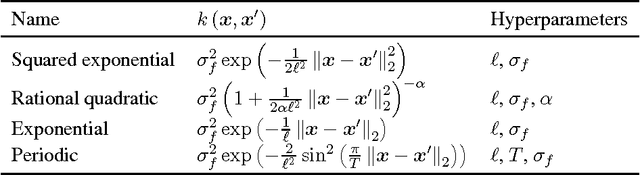
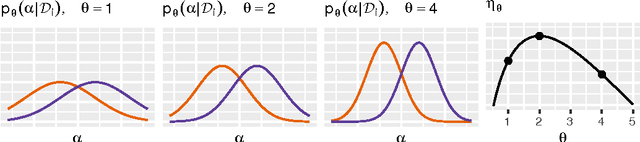
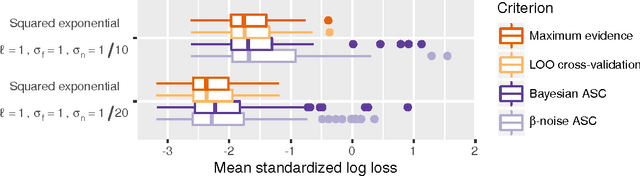
Gaussian processes are powerful, yet analytically tractable models for supervised learning. A Gaussian process is characterized by a mean function and a covariance function (kernel), which are determined by a model selection criterion. The functions to be compared do not just differ in their parametrization but in their fundamental structure. It is often not clear which function structure to choose, for instance to decide between a squared exponential and a rational quadratic kernel. Based on the principle of approximation set coding, we develop a framework for model selection to rank kernels for Gaussian process regression. In our experiments approximation set coding shows promise to become a model selection criterion competitive with maximum evidence (also called marginal likelihood) and leave-one-out cross-validation.