Prompt Programming: A Platform for Dialogue-based Computational Problem Solving with Generative AI Models

Computing students increasingly rely on generative AI tools for programming assistance, often without formal instruction or guidance. This highlights a need to teach students how to effectively interact with AI models, particularly through natural language prompts, to generate and critically evaluate code for solving computational tasks. To address this, we developed a novel platform for prompt programming that enables authentic dialogue-based interactions, supports problems involving multiple interdependent functions, and offers on-request execution of generated code. Data analysis from over 900 students in an introductory programming course revealed high engagement, with the majority of prompts occurring within multi-turn dialogues. Problems with multiple interdependent functions encouraged iterative refinement, with progression graphs highlighting several common strategies. Students were highly selective about the code they chose to test, suggesting that on-request execution of generated code promoted critical thinking. Given the growing importance of learning dialogue-based programming with AI, we provide this tool as a publicly accessible resource, accompanied by a corpus of programming problems for educational use.

Hints-In-Browser: Benchmarking Language Models for Programming Feedback Generation

Generative AI and large language models hold great promise in enhancing programming education by generating individualized feedback and hints for learners. Recent works have primarily focused on improving the quality of generated feedback to achieve human tutors' quality. While quality is an important performance criterion, it is not the only criterion to optimize for real-world educational deployments. In this paper, we benchmark language models for programming feedback generation across several performance criteria, including quality, cost, time, and data privacy. The key idea is to leverage recent advances in the new paradigm of in-browser inference that allow running these models directly in the browser, thereby providing direct benefits across cost and data privacy. To boost the feedback quality of small models compatible with in-browser inference engines, we develop a fine-tuning pipeline based on GPT-4 generated synthetic data. We showcase the efficacy of fine-tuned Llama3-8B and Phi3-3.8B 4-bit quantized models using WebLLM's in-browser inference engine on three different Python programming datasets. We will release the full implementation along with a web app and datasets to facilitate further research on in-browser language models.

On the Existence of Universal Lottery Tickets

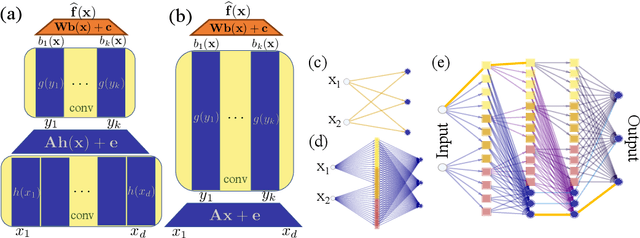
The lottery ticket hypothesis conjectures the existence of sparse subnetworks of large randomly initialized deep neural networks that can be successfully trained in isolation. Recent work has experimentally observed that some of these tickets can be practically reused across a variety of tasks, hinting at some form of universality. We formalize this concept and theoretically prove that not only do such universal tickets exist but they also do not require further training. Our proofs introduce a couple of technical innovations related to pruning for strong lottery tickets, including extensions of subset sum results and a strategy to leverage higher amounts of depth. Our explicit sparse constructions of universal function families might be of independent interest, as they highlight representational benefits induced by univariate convolutional architectures.

Scaling up Continuous-Time Markov Chains Helps Resolve Underspecification

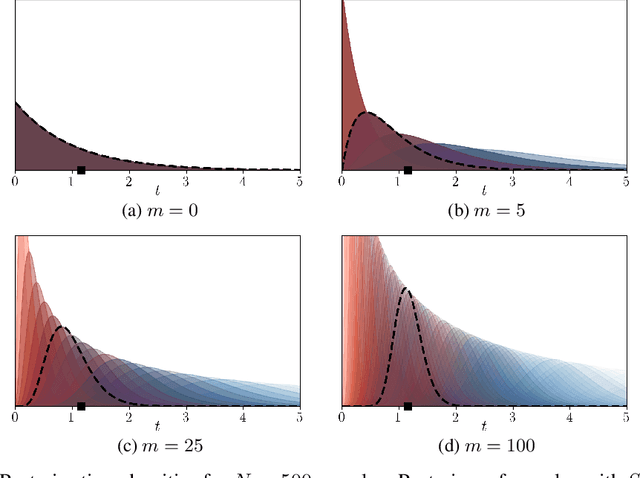
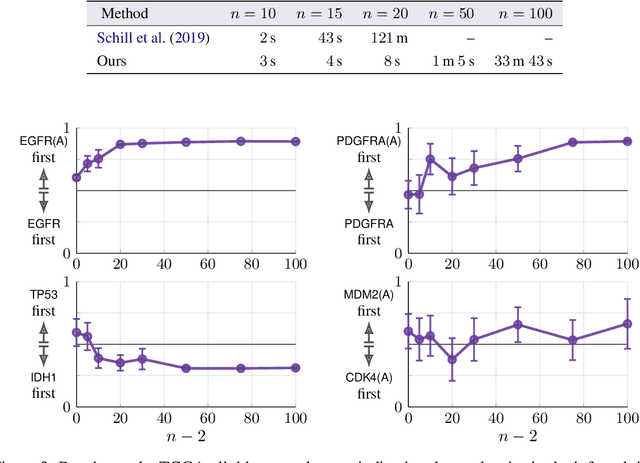
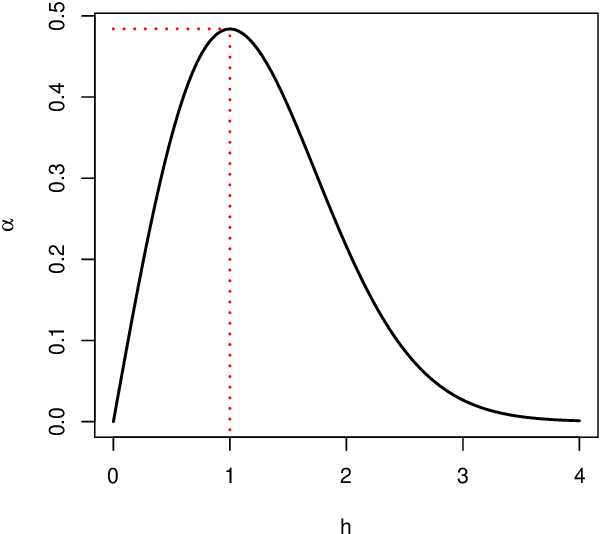
Modeling the time evolution of discrete sets of items (e.g., genetic mutations) is a fundamental problem in many biomedical applications. We approach this problem through the lens of continuous-time Markov chains, and show that the resulting learning task is generally underspecified in the usual setting of cross-sectional data. We explore a perhaps surprising remedy: including a number of additional independent items can help determine time order, and hence resolve underspecification. This is in sharp contrast to the common practice of limiting the analysis to a small subset of relevant items, which is followed largely due to poor scaling of existing methods. To put our theoretical insight into practice, we develop an approximate likelihood maximization method for learning continuous-time Markov chains, which can scale to hundreds of items and is orders of magnitude faster than previous methods. We demonstrate the effectiveness of our approach on synthetic and real cancer data.

Strong Log-Concavity Does Not Imply Log-Submodularity

We disprove a recent conjecture regarding discrete distributions and their generating polynomials stating that strong log-concavity implies log-submodularity.

Discrete Sampling using Semigradient-based Product Mixtures

We consider the problem of inference in discrete probabilistic models, that is, distributions over subsets of a finite ground set. These encompass a range of well-known models in machine learning, such as determinantal point processes and Ising models. Locally-moving Markov chain Monte Carlo algorithms, such as the Gibbs sampler, are commonly used for inference in such models, but their convergence is, at times, prohibitively slow. This is often caused by state-space bottlenecks that greatly hinder the movement of such samplers. We propose a novel sampling strategy that uses a specific mixture of product distributions to propose global moves and, thus, accelerate convergence. Furthermore, we show how to construct such a mixture using semigradient information. We illustrate the effectiveness of combining our sampler with existing ones, both theoretically on an example model, as well as practically on three models learned from real-world data sets.

Fast Gaussian Process Based Gradient Matching for Parameter Identification in Systems of Nonlinear ODEs

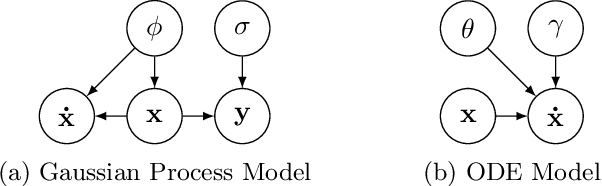
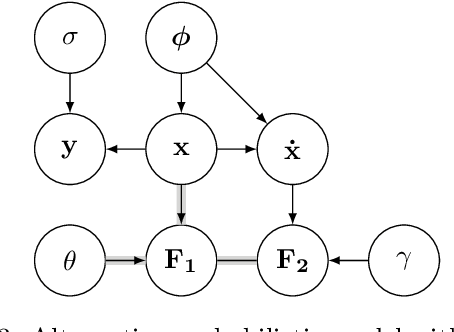
Parameter identification and comparison of dynamical systems is a challenging task in many fields. Bayesian approaches based on Gaussian process regression over time-series data have been successfully applied to infer the parameters of a dynamical system without explicitly solving it. While the benefits in computational cost are well established, a rigorous mathematical framework has been missing. We offer a novel interpretation which leads to a better understanding and improvements in state-of-the-art performance in terms of accuracy for nonlinear dynamical systems.