Method-of-Moments Inference for GLMs and Doubly Robust Functionals under Proportional Asymptotics

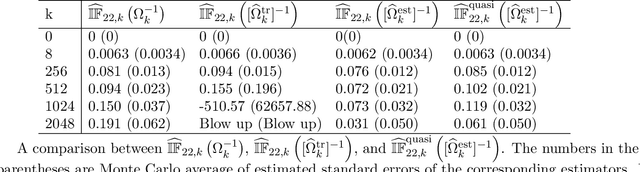
In this paper, we consider the estimation of regression coefficients and signal-to-noise (SNR) ratio in high-dimensional Generalized Linear Models (GLMs), and explore their implications in inferring popular estimands such as average treatment effects in high-dimensional observational studies. Under the ``proportional asymptotic'' regime and Gaussian covariates with known (population) covariance $\Sigma$, we derive Consistent and Asymptotically Normal (CAN) estimators of our targets of inference through a Method-of-Moments type of estimators that bypasses estimation of high dimensional nuisance functions and hyperparameter tuning altogether. Additionally, under non-Gaussian covariates, we demonstrate universality of our results under certain additional assumptions on the regression coefficients and $\Sigma$. We also demonstrate that knowing $\Sigma$ is not essential to our proposed methodology when the sample covariance matrix estimator is invertible. Finally, we complement our theoretical results with numerical experiments and comparisons with existing literature.

Can we falsify the justification of the validity of Wald confidence intervals of doubly robust functionals, without assumptions?

In this article we develop a feasible version of the assumption-lean tests in Liu et al. 20 that can falsify an analyst's justification for the validity of a reported nominal $(1 - \alpha)$ Wald confidence interval (CI) centered at a double machine learning (DML) estimator for any member of the class of doubly robust (DR) functionals studied by Rotnitzky et al. 21. The class of DR functionals is broad and of central importance in economics and biostatistics. It strictly includes both (i) the class of mean-square continuous functionals that can be written as an expectation of an affine functional of a conditional expectation studied by Chernozhukov et al. 22 and the class of functionals studied by Robins et al. 08. The present state-of-the-art estimators for DR functionals $\psi$ are DML estimators $\hat{\psi}_{1}$. The bias of $\hat{\psi}_{1}$ depends on the product of the rates at which two nuisance functions $b$ and $p$ are estimated. Most commonly an analyst justifies the validity of her Wald CIs by proving that, under her complexity-reducing assumptions, the Cauchy-Schwarz (CS) upper bound for the bias of $\hat{\psi}_{1}$ is $o (n^{- 1 / 2})$. Thus if the hypothesis $H_{0}$: the CS upper bound is $o (n^{- 1 / 2})$ is rejected by our test, we will have falsified the analyst's justification for the validity of her Wald CIs. In this work, we exhibit a valid assumption-lean falsification test of $H_{0}$, without relying on complexity-reducing assumptions on $b, p$, or their estimates $\hat{b}, \hat{p}$. Simulation experiments are conducted to demonstrate how the proposed assumption-lean test can be used in practice. An unavoidable limitation of our methodology is that no assumption-lean test of $H_{0}$, including ours, can be a consistent test. Thus failure of our test to reject is not meaningful evidence in favor of $H_{0}$.

On Undersmoothing and Sample Splitting for Estimating a Doubly Robust Functional

We consider the problem of constructing minimax rate-optimal estimators for a doubly robust nonparametric functional that has witnessed applications across the causal inference and conditional independence testing literature. Minimax rate-optimal estimators for such functionals are typically constructed through higher-order bias corrections of plug-in and one-step type estimators and, in turn, depend on estimators of nuisance functions. In this paper, we consider a parallel question of interest regarding the optimality and/or sub-optimality of plug-in and one-step bias-corrected estimators for the specific doubly robust functional of interest. Specifically, we verify that by using undersmoothing and sample splitting techniques when constructing nuisance function estimators, one can achieve minimax rates of convergence in all H\"older smoothness classes of the nuisance functions (i.e. the propensity score and outcome regression) provided that the marginal density of the covariates is sufficiently regular. Additionally, by demonstrating suitable lower bounds on these classes of estimators, we demonstrate the necessity to undersmooth the nuisance function estimators to obtain minimax optimal rates of convergence.

Sparse Signal Detection in Heteroscedastic Gaussian Sequence Models: Sharp Minimax Rates

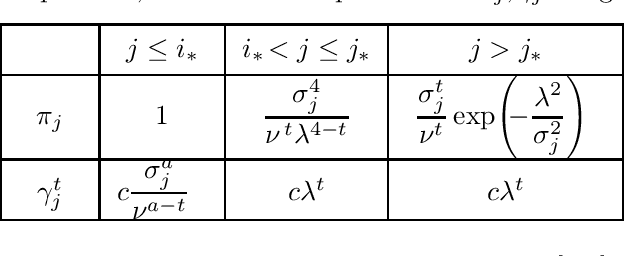
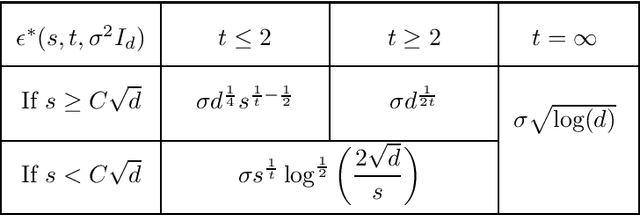
Given a heterogeneous Gaussian sequence model with unknown mean $\theta \in \mathbb R^d$ and known covariance matrix $\Sigma = \operatorname{diag}(\sigma_1^2,\dots, \sigma_d^2)$, we study the signal detection problem against sparse alternatives, for known sparsity $s$. Namely, we characterize how large $\epsilon^*>0$ should be, in order to distinguish with high probability the null hypothesis $\theta=0$ from the alternative composed of $s$-sparse vectors in $\mathbb R^d$, separated from $0$ in $L^t$ norm ($t \geq 1$) by at least $\epsilon^*$. We find minimax upper and lower bounds over the minimax separation radius $\epsilon^*$ and prove that they are always matching. We also derive the corresponding minimax tests achieving these bounds. Our results reveal new phase transitions regarding the behavior of $\epsilon^*$ with respect to the level of sparsity, to the $L^t$ metric, and to the heteroscedasticity profile of $\Sigma$. In the case of the Euclidean (i.e. $L^2$) separation, we bridge the remaining gaps in the literature.

A New Central Limit Theorem for the Augmented IPW Estimator: Variance Inflation, Cross-Fit Covariance and Beyond

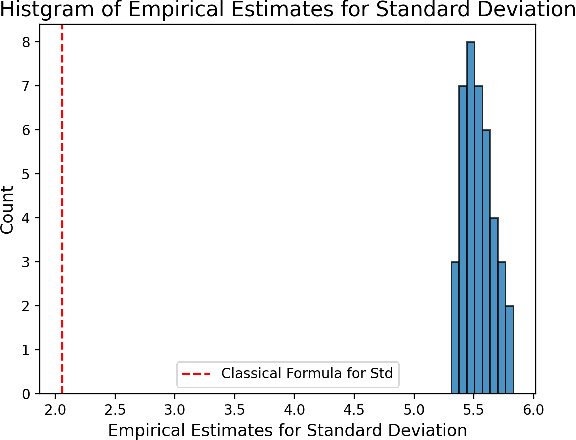
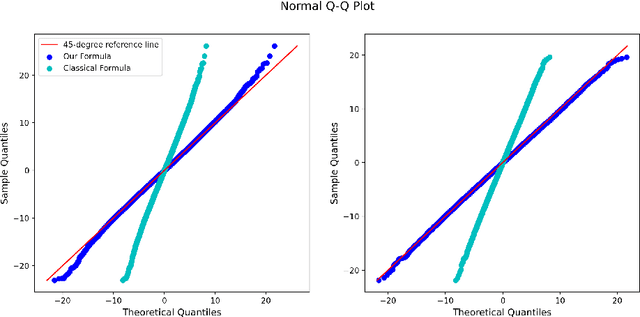
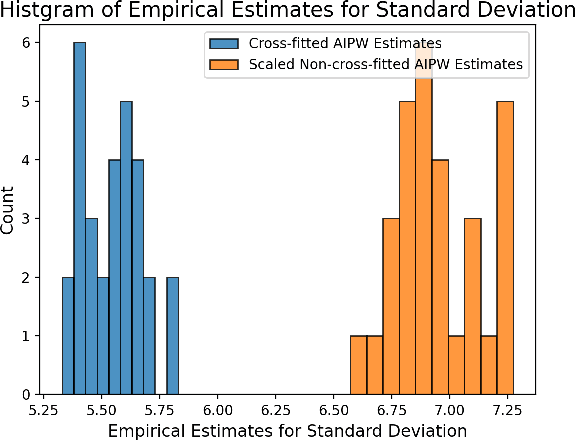
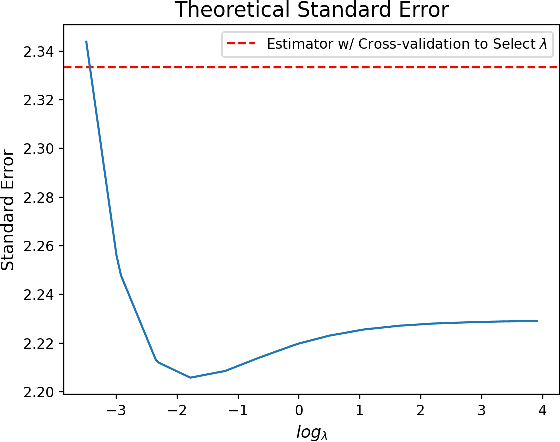
Estimation of the average treatment effect (ATE) is a central problem in causal inference. In recent times, inference for the ATE in the presence of high-dimensional covariates has been extensively studied. Among the diverse approaches that have been proposed, augmented inverse probability weighting (AIPW) with cross-fitting has emerged as a popular choice in practice. In this work, we study this cross-fit AIPW estimator under well-specified outcome regression and propensity score models in a high-dimensional regime where the number of features and samples are both large and comparable. Under assumptions on the covariate distribution, we establish a new CLT for the suitably scaled cross-fit AIPW that applies without any sparsity assumptions on the underlying high-dimensional parameters. Our CLT uncovers two crucial phenomena among others: (i) the AIPW exhibits a substantial variance inflation that can be precisely quantified in terms of the signal-to-noise ratio and other problem parameters, (ii) the asymptotic covariance between the pre-cross-fit estimates is non-negligible even on the root-n scale. In fact, these cross-covariances turn out to be negative in our setting. These findings are strikingly different from their classical counterparts. On the technical front, our work utilizes a novel interplay between three distinct tools--approximate message passing theory, the theory of deterministic equivalents, and the leave-one-out approach. We believe our proof techniques should be useful for analyzing other two-stage estimators in this high-dimensional regime. Finally, we complement our theoretical results with simulations that demonstrate both the finite sample efficacy of our CLT and its robustness to our assumptions.

On the Existence of Universal Lottery Tickets

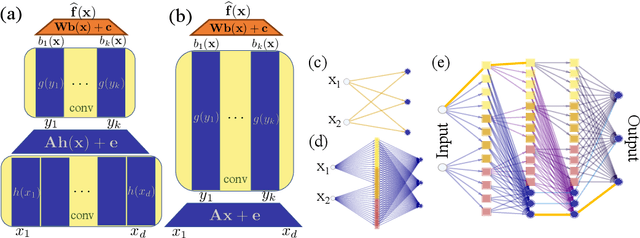
The lottery ticket hypothesis conjectures the existence of sparse subnetworks of large randomly initialized deep neural networks that can be successfully trained in isolation. Recent work has experimentally observed that some of these tickets can be practically reused across a variety of tasks, hinting at some form of universality. We formalize this concept and theoretically prove that not only do such universal tickets exist but they also do not require further training. Our proofs introduce a couple of technical innovations related to pruning for strong lottery tickets, including extensions of subset sum results and a strategy to leverage higher amounts of depth. Our explicit sparse constructions of universal function families might be of independent interest, as they highlight representational benefits induced by univariate convolutional architectures.

Cross-Cluster Weighted Forests

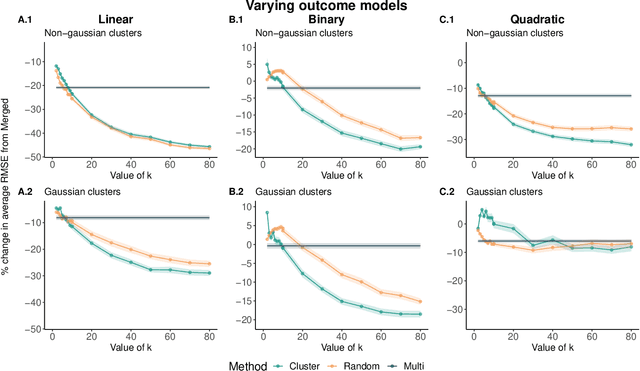
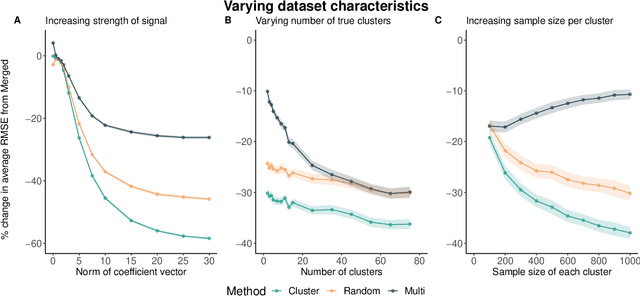
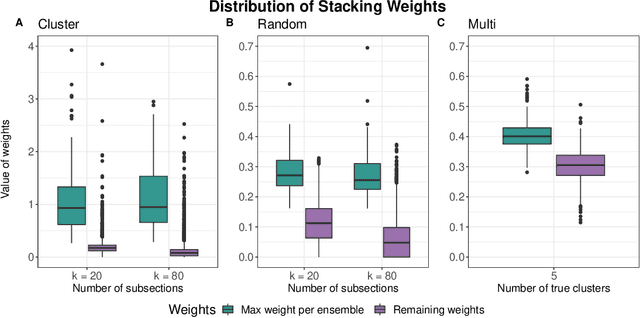
Adapting machine learning algorithms to better handle the presence of natural clustering or batch effects within training datasets is imperative across a wide variety of biological applications. This article considers the effect of ensembling Random Forest learners trained on clusters within a single dataset with heterogeneity in the distribution of the features. We find that constructing ensembles of forests trained on clusters determined by algorithms such as k-means results in significant improvements in accuracy and generalizability over the traditional Random Forest algorithm. We denote our novel approach as the Cross-Cluster Weighted Forest, and examine its robustness to various data-generating scenarios and outcome models. Furthermore, we explore the influence of the data-partitioning and ensemble weighting strategies on conferring the benefits of our method over the existing paradigm. Finally, we apply our approach to cancer molecular profiling and gene expression datasets that are naturally divisible into clusters and illustrate that our approach outperforms classic Random Forest. Code and supplementary material are available at https://github.com/m-ramchandran/cross-cluster.

Semi-Supervised Off Policy Reinforcement Learning

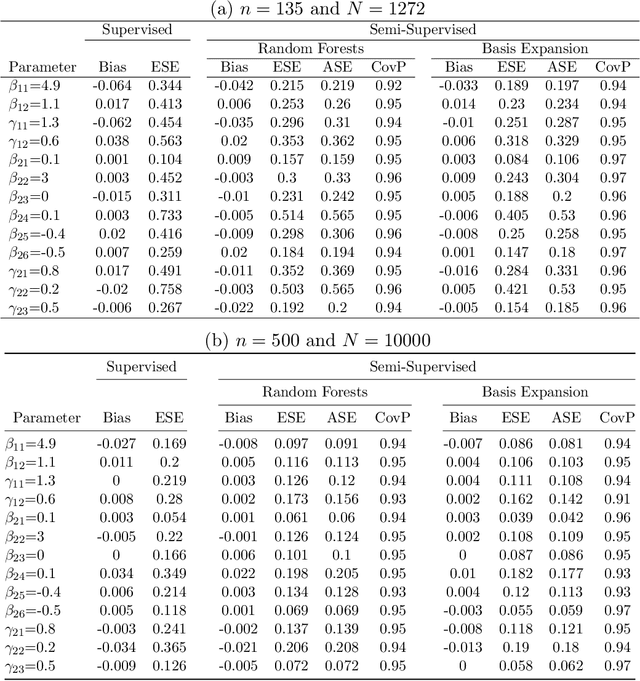
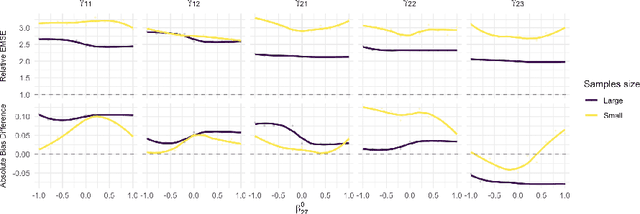
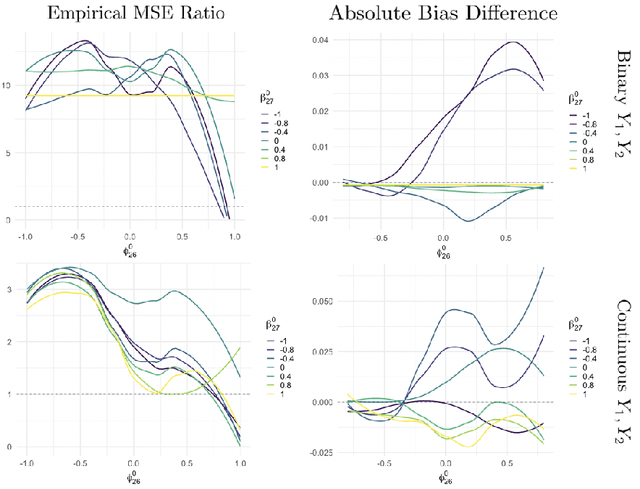
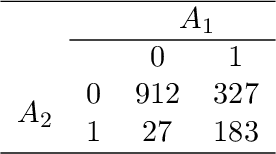
Reinforcement learning (RL) has shown great success in estimating sequential treatment strategies which account for patient heterogeneity. However, health-outcome information is often not well coded but rather embedded in clinical notes. Extracting precise outcome information is a resource intensive task. This translates into only small well-annotated cohorts available. We propose a semi-supervised learning (SSL) approach that can efficiently leverage a small sized labeled data $\mathcal{L}$ with true outcome observed, and a large sized unlabeled data $\mathcal{U}$ with outcome surrogates $\pmb W$. In particular we propose a theoretically justified SSL approach to Q-learning and develop a robust and efficient SSL approach to estimating the value function of the derived optimal STR, defined as the expected counterfactual outcome under the optimal STR. Generalizing SSL to learning STR brings interesting challenges. First, the feature distribution for predicting $Y_t$ is unknown in the $Q$-learning procedure, as it includes unknown $Y_{t-1}$ due to the sequential nature. Our methods for estimating optimal STR and its associated value function, carefully adapts to this sequentially missing data structure. Second, we modify the SSL framework to handle the use of surrogate variables $\pmb W$ which are predictive of the outcome through the joint law $\mathbb{P}_{Y,\pmb O,\pmb W}$, but are not part of the conditional distribution of interest $\mathbb{P}_{Y|\pmb O}$. We provide theoretical results to understand when and to what degree efficiency can be gained from $\pmb W$ and $\pmb O$. Our approach is robust to misspecification of the imputation models. Further, we provide a doubly robust value function estimator for the derived STR. If either the Q functions or the propensity score functions are correctly specified, our value function estimators are consistent for the true value function.

Rejoinder: On nearly assumption-free tests of nominal confidence interval coverage for causal parameters estimated by machine learning

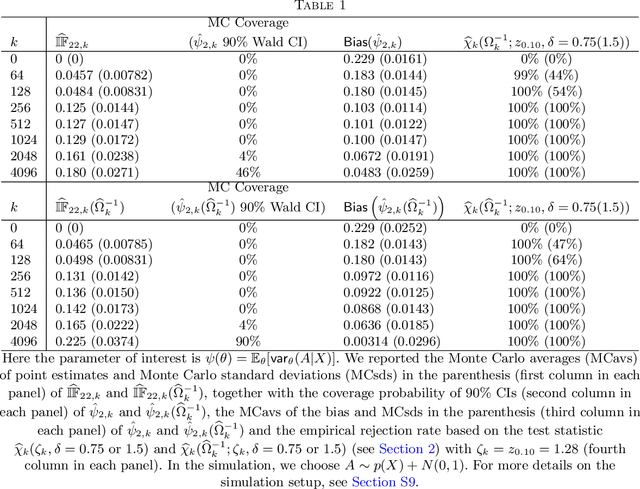
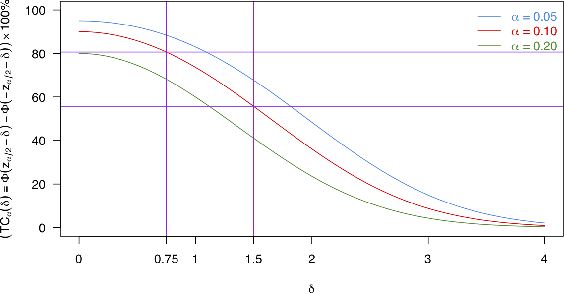
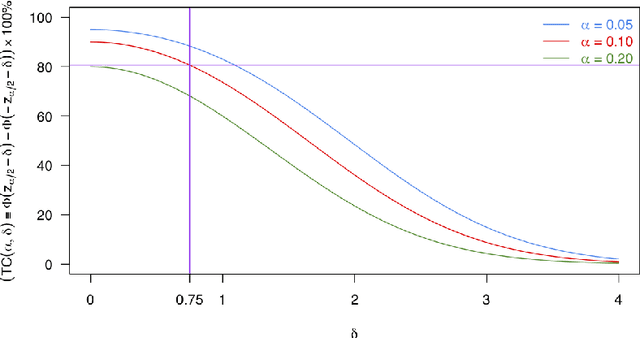
This is the rejoinder to the discussion by Kennedy, Balakrishnan and Wasserman on the paper "On nearly assumption-free tests of nominal confidence interval coverage for causal parameters estimated by machine learning" published in Statistical Science.

On assumption-free tests and confidence intervals for causal effects estimated by machine learning

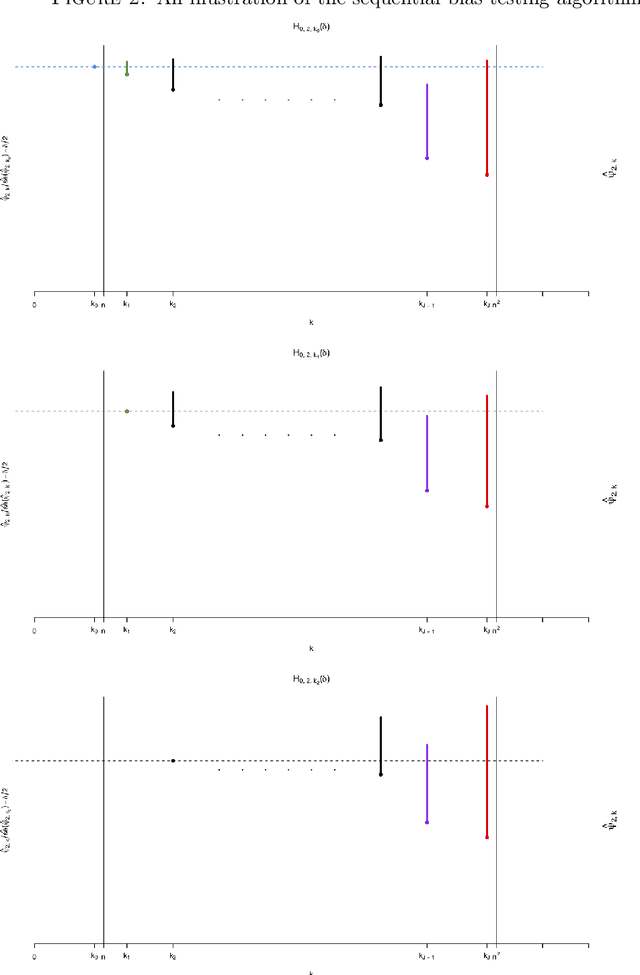
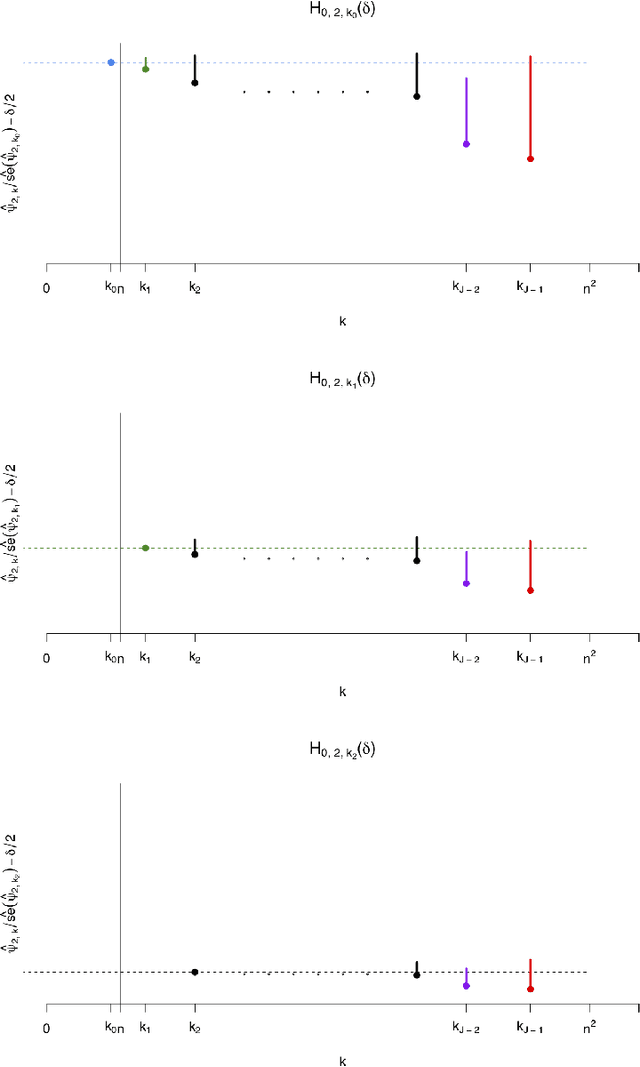
For many causal effect parameters $\psi$ of interest doubly robust machine learning estimators $\widehat\psi_1$ are the state-of-the-art, incorporating the benefits of the low prediction error of machine learning algorithms; the decreased bias of doubly robust estimators; and.the analytic tractability and bias reduction of cross fitting. When the potential confounders is high dimensional, the associated $(1 - \alpha)$ Wald intervals may still undercover even in large samples, because the bias may be of the same or even larger order than its standard error. In this paper, we introduce tests that can have the power to detect whether the bias of $\widehat\psi_1$ is of the same or even larger order than its standard error of order $n^{-1/2}$, can provide a lower confidence limit on the degree of under coverage of the interval and strikingly, are valid under essentially no assumptions. We also introduce an estimator with bias generally less than that of $\widehat\psi_1$, yet whose standard error is not much greater than $\widehat\psi_1$'s. The tests, as well as the estimator $\widehat\psi_2$, are based on a U-statistic that is the second-order influence function for the parameter that encodes the estimable part of the bias of $\widehat\psi_1$. Our impressive claims need to be tempered in several important ways. First no test, including ours, of the null hypothesis that the ratio of the bias to its standard error can be consistent [without making additional assumptions that may be incorrect]. Furthermore the above claims only apply to parameters in a particular class. For the others, our results are less sharp and require more careful interpretation.