Nilanjana Laha
On the Existence of Universal Lottery Tickets
Nov 22, 2021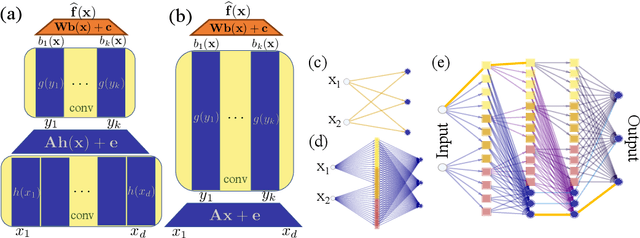
Abstract:The lottery ticket hypothesis conjectures the existence of sparse subnetworks of large randomly initialized deep neural networks that can be successfully trained in isolation. Recent work has experimentally observed that some of these tickets can be practically reused across a variety of tasks, hinting at some form of universality. We formalize this concept and theoretically prove that not only do such universal tickets exist but they also do not require further training. Our proofs introduce a couple of technical innovations related to pruning for strong lottery tickets, including extensions of subset sum results and a strategy to leverage higher amounts of depth. Our explicit sparse constructions of universal function families might be of independent interest, as they highlight representational benefits induced by univariate convolutional architectures.
Semi-Supervised Off Policy Reinforcement Learning
Jan 21, 2021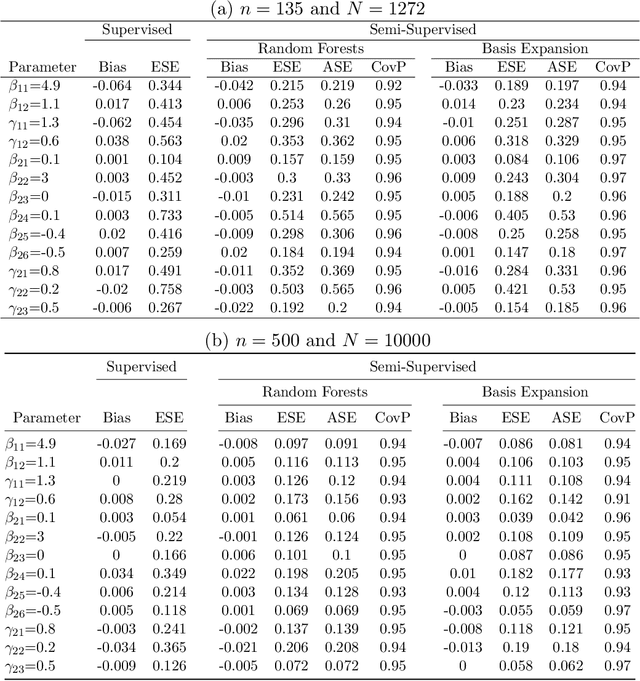
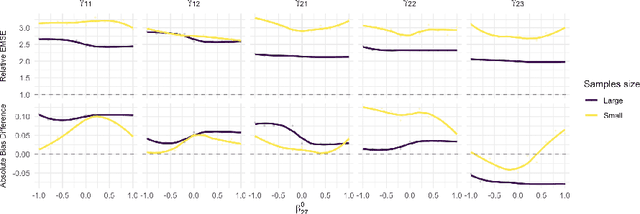
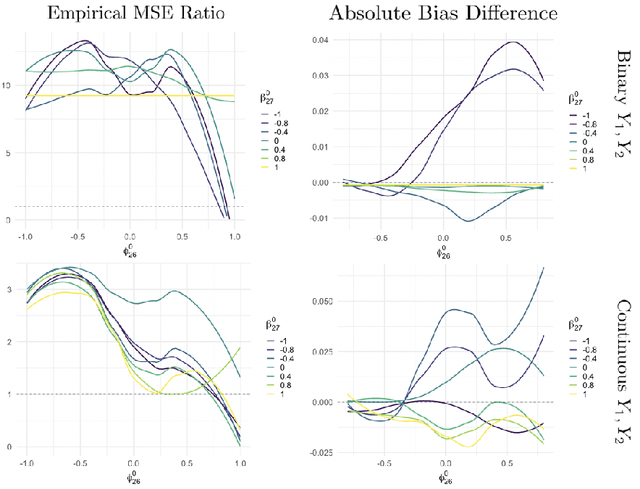
Abstract:Reinforcement learning (RL) has shown great success in estimating sequential treatment strategies which account for patient heterogeneity. However, health-outcome information is often not well coded but rather embedded in clinical notes. Extracting precise outcome information is a resource intensive task. This translates into only small well-annotated cohorts available. We propose a semi-supervised learning (SSL) approach that can efficiently leverage a small sized labeled data $\mathcal{L}$ with true outcome observed, and a large sized unlabeled data $\mathcal{U}$ with outcome surrogates $\pmb W$. In particular we propose a theoretically justified SSL approach to Q-learning and develop a robust and efficient SSL approach to estimating the value function of the derived optimal STR, defined as the expected counterfactual outcome under the optimal STR. Generalizing SSL to learning STR brings interesting challenges. First, the feature distribution for predicting $Y_t$ is unknown in the $Q$-learning procedure, as it includes unknown $Y_{t-1}$ due to the sequential nature. Our methods for estimating optimal STR and its associated value function, carefully adapts to this sequentially missing data structure. Second, we modify the SSL framework to handle the use of surrogate variables $\pmb W$ which are predictive of the outcome through the joint law $\mathbb{P}_{Y,\pmb O,\pmb W}$, but are not part of the conditional distribution of interest $\mathbb{P}_{Y|\pmb O}$. We provide theoretical results to understand when and to what degree efficiency can be gained from $\pmb W$ and $\pmb O$. Our approach is robust to misspecification of the imputation models. Further, we provide a doubly robust value function estimator for the derived STR. If either the Q functions or the propensity score functions are correctly specified, our value function estimators are consistent for the true value function.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge