Federated Offline Reinforcement Learning

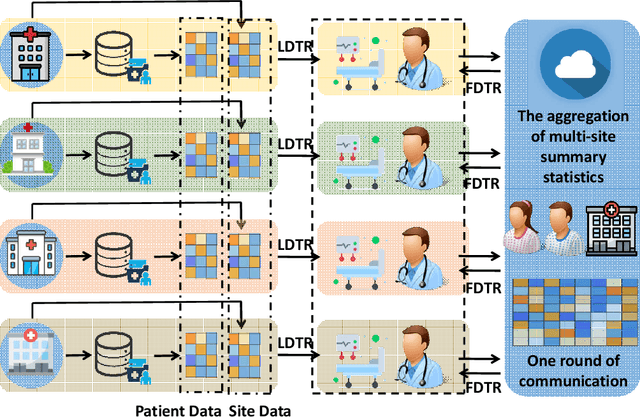
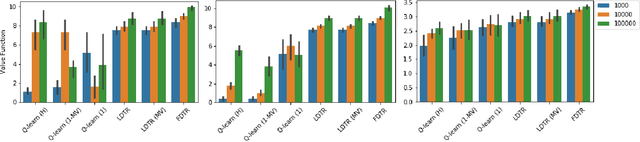
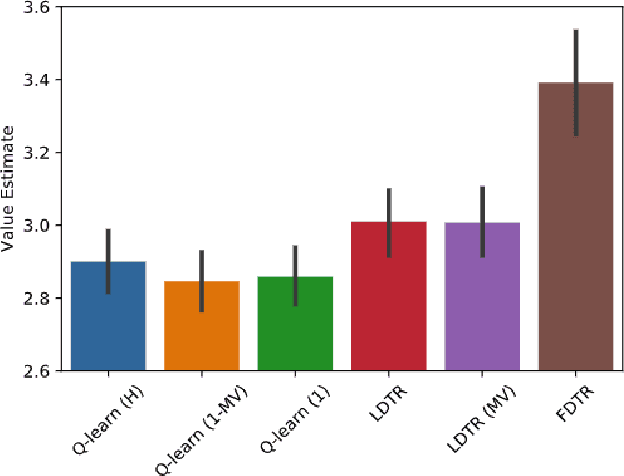
Evidence-based or data-driven dynamic treatment regimes are essential for personalized medicine, which can benefit from offline reinforcement learning (RL). Although massive healthcare data are available across medical institutions, they are prohibited from sharing due to privacy constraints. Besides, heterogeneity exists in different sites. As a result, federated offline RL algorithms are necessary and promising to deal with the problems. In this paper, we propose a multi-site Markov decision process model which allows both homogeneous and heterogeneous effects across sites. The proposed model makes the analysis of the site-level features possible. We design the first federated policy optimization algorithm for offline RL with sample complexity. The proposed algorithm is communication-efficient and privacy-preserving, which requires only a single round of communication interaction by exchanging summary statistics. We give a theoretical guarantee for the proposed algorithm without the assumption of sufficient action coverage, where the suboptimality for the learned policies is comparable to the rate as if data is not distributed. Extensive simulations demonstrate the effectiveness of the proposed algorithm. The method is applied to a sepsis data set in multiple sites to illustrate its use in clinical settings.

Semi-Supervised Off Policy Reinforcement Learning

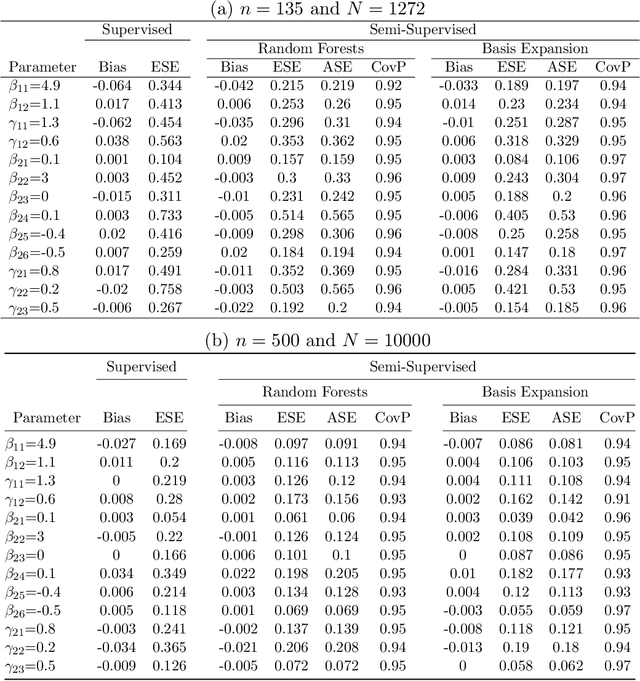
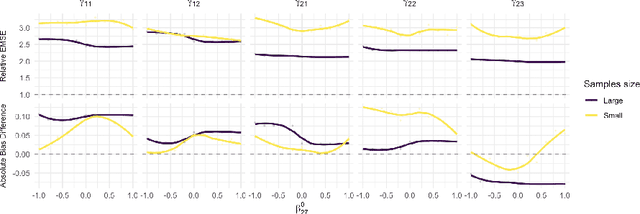
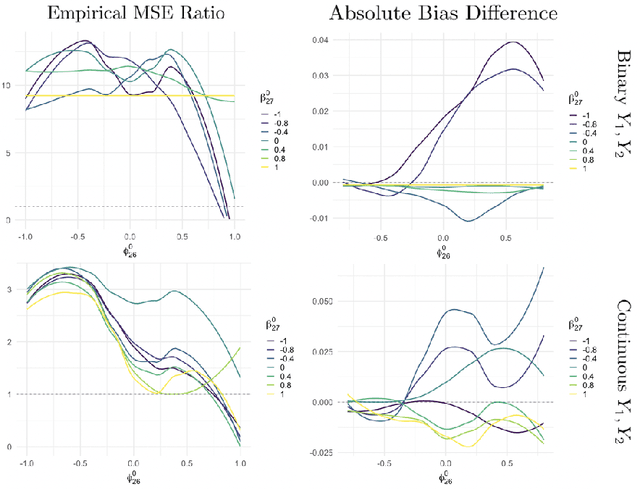
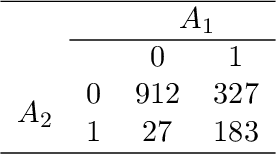
Reinforcement learning (RL) has shown great success in estimating sequential treatment strategies which account for patient heterogeneity. However, health-outcome information is often not well coded but rather embedded in clinical notes. Extracting precise outcome information is a resource intensive task. This translates into only small well-annotated cohorts available. We propose a semi-supervised learning (SSL) approach that can efficiently leverage a small sized labeled data $\mathcal{L}$ with true outcome observed, and a large sized unlabeled data $\mathcal{U}$ with outcome surrogates $\pmb W$. In particular we propose a theoretically justified SSL approach to Q-learning and develop a robust and efficient SSL approach to estimating the value function of the derived optimal STR, defined as the expected counterfactual outcome under the optimal STR. Generalizing SSL to learning STR brings interesting challenges. First, the feature distribution for predicting $Y_t$ is unknown in the $Q$-learning procedure, as it includes unknown $Y_{t-1}$ due to the sequential nature. Our methods for estimating optimal STR and its associated value function, carefully adapts to this sequentially missing data structure. Second, we modify the SSL framework to handle the use of surrogate variables $\pmb W$ which are predictive of the outcome through the joint law $\mathbb{P}_{Y,\pmb O,\pmb W}$, but are not part of the conditional distribution of interest $\mathbb{P}_{Y|\pmb O}$. We provide theoretical results to understand when and to what degree efficiency can be gained from $\pmb W$ and $\pmb O$. Our approach is robust to misspecification of the imputation models. Further, we provide a doubly robust value function estimator for the derived STR. If either the Q functions or the propensity score functions are correctly specified, our value function estimators are consistent for the true value function.