On assumption-free tests and confidence intervals for causal effects estimated by machine learning
Paper and Code
Apr 08, 2019
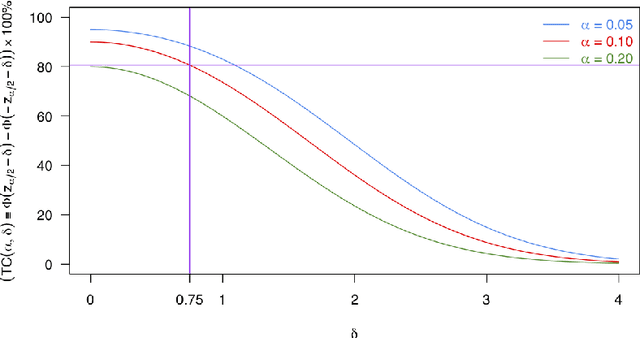
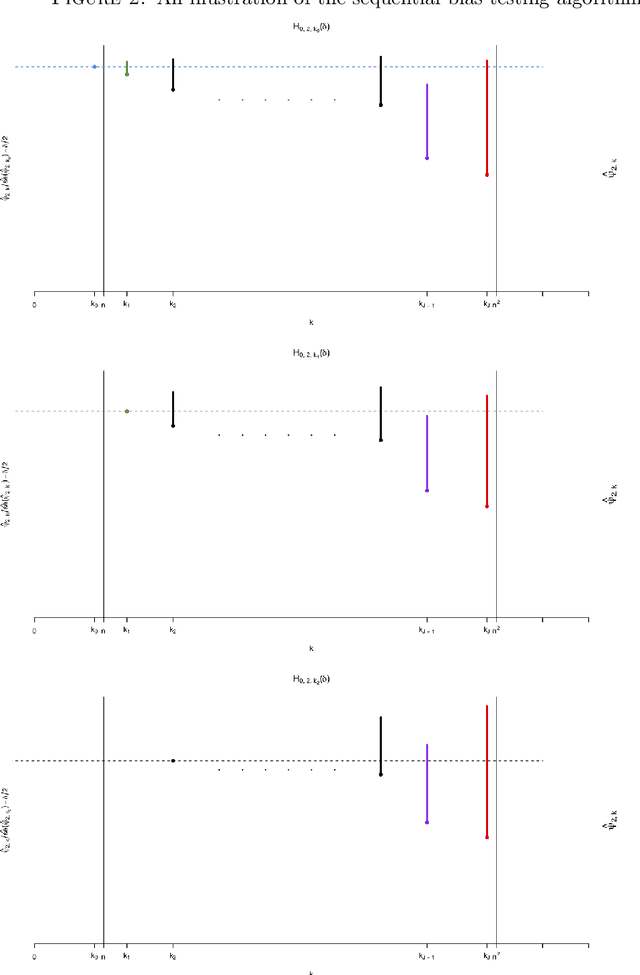
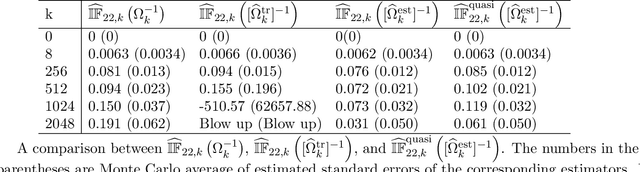
For many causal effect parameters $\psi$ of interest doubly robust machine learning estimators $\widehat\psi_1$ are the state-of-the-art, incorporating the benefits of the low prediction error of machine learning algorithms; the decreased bias of doubly robust estimators; and.the analytic tractability and bias reduction of cross fitting. When the potential confounders is high dimensional, the associated $(1 - \alpha)$ Wald intervals may still undercover even in large samples, because the bias may be of the same or even larger order than its standard error. In this paper, we introduce tests that can have the power to detect whether the bias of $\widehat\psi_1$ is of the same or even larger order than its standard error of order $n^{-1/2}$, can provide a lower confidence limit on the degree of under coverage of the interval and strikingly, are valid under essentially no assumptions. We also introduce an estimator with bias generally less than that of $\widehat\psi_1$, yet whose standard error is not much greater than $\widehat\psi_1$'s. The tests, as well as the estimator $\widehat\psi_2$, are based on a U-statistic that is the second-order influence function for the parameter that encodes the estimable part of the bias of $\widehat\psi_1$. Our impressive claims need to be tempered in several important ways. First no test, including ours, of the null hypothesis that the ratio of the bias to its standard error can be consistent [without making additional assumptions that may be incorrect]. Furthermore the above claims only apply to parameters in a particular class. For the others, our results are less sharp and require more careful interpretation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge