Multi-source domain adaptation for regression

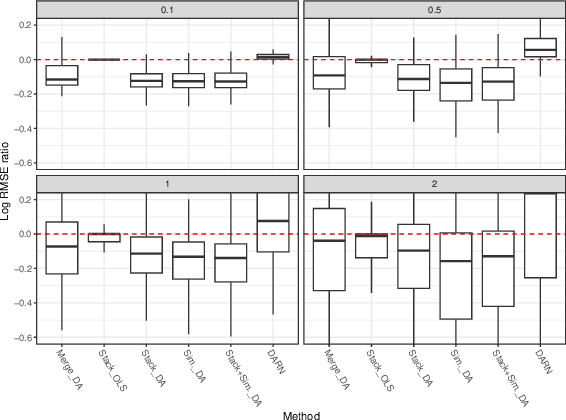
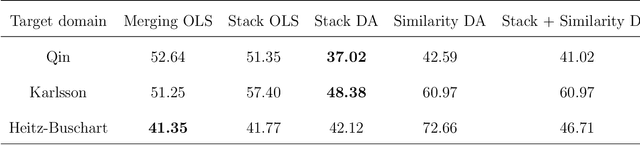
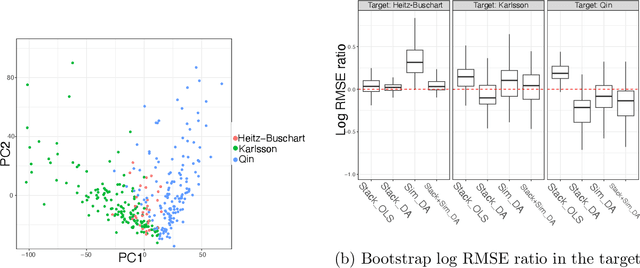
Multi-source domain adaptation (DA) aims at leveraging information from more than one source domain to make predictions in a target domain, where different domains may have different data distributions. Most existing methods for multi-source DA focus on classification problems while there is only limited investigation in the regression settings. In this paper, we fill in this gap through a two-step procedure. First, we extend a flexible single-source DA algorithm for classification through outcome-coarsening to enable its application to regression problems. We then augment our single-source DA algorithm for regression with ensemble learning to achieve multi-source DA. We consider three learning paradigms in the ensemble algorithm, which combines linearly the target-adapted learners trained with each source domain: (i) a multi-source stacking algorithm to obtain the ensemble weights; (ii) a similarity-based weighting where the weights reflect the quality of DA of each target-adapted learner; and (iii) a combination of the stacking and similarity weights. We illustrate the performance of our algorithms with simulations and a data application where the goal is to predict High-density lipoprotein (HDL) cholesterol levels using gut microbiome. We observe a consistent improvement in prediction performance of our multi-source DA algorithm over the routinely used methods in all these scenarios.

Multi-study R-learner for Heterogeneous Treatment Effect Estimation

Estimating heterogeneous treatment effects is crucial for informing personalized treatment strategies and policies. While multiple studies can improve the accuracy and generalizability of results, leveraging them for estimation is statistically challenging. Existing approaches often assume identical heterogeneous treatment effects across studies, but this may be violated due to various sources of between-study heterogeneity, including differences in study design, confounders, and sample characteristics. To this end, we propose a unifying framework for multi-study heterogeneous treatment effect estimation that is robust to between-study heterogeneity in the nuisance functions and treatment effects. Our approach, the multi-study R-learner, extends the R-learner to obtain principled statistical estimation with modern machine learning (ML) in the multi-study setting. The multi-study R-learner is easy to implement and flexible in its ability to incorporate ML for estimating heterogeneous treatment effects, nuisance functions, and membership probabilities, which borrow strength across heterogeneous studies. It achieves robustness in confounding adjustment through its loss function and can leverage both randomized controlled trials and observational studies. We provide asymptotic guarantees for the proposed method in the case of series estimation and illustrate using real cancer data that it has the lowest estimation error compared to existing approaches in the presence of between-study heterogeneity.

Defining Replicability of Prediction Rules

In this article I propose an approach for defining replicability for prediction rules. Motivated by a recent NAS report, I start from the perspective that replicability is obtaining consistent results across studies suitable to address the same prediction question, each of which has obtained its own data. I then discuss concept and issues in defining key elements of this statement. I focus specifically on the meaning of "consistent results" in typical utilization contexts, and propose a multi-agent framework for defining replicability, in which agents are neither partners nor adversaries. I recover some of the prevalent practical approaches as special cases. I hope to provide guidance for a more systematic assessment of replicability in machine learning.

Multi-Task Learning for Sparsity Pattern Heterogeneity: A Discrete Optimization Approach

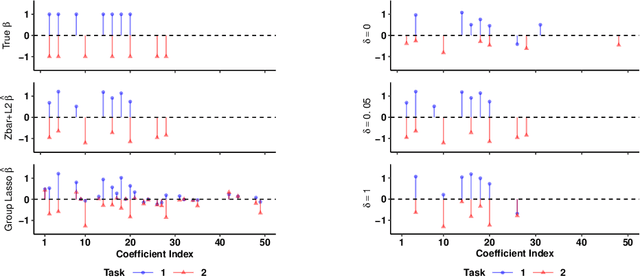
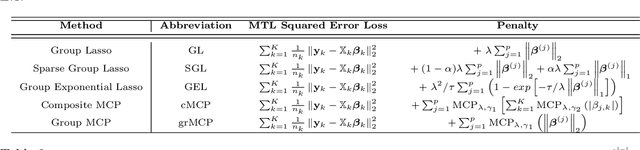
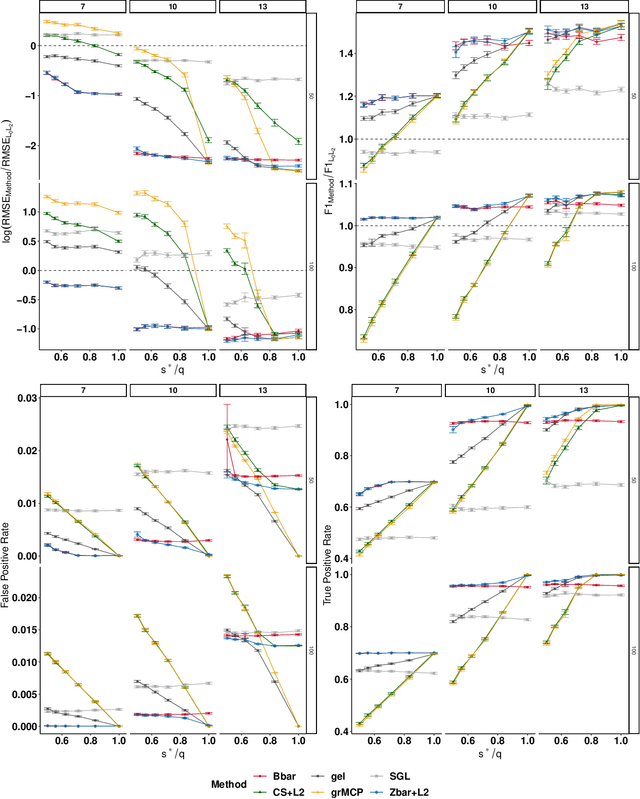
We extend best-subset selection to linear Multi-Task Learning (MTL), where a set of linear models are jointly trained on a collection of datasets (``tasks''). Allowing the regression coefficients of tasks to have different sparsity patterns (i.e., different supports), we propose a modeling framework for MTL that encourages models to share information across tasks, for a given covariate, through separately 1) shrinking the coefficient supports together, and/or 2) shrinking the coefficient values together. This allows models to borrow strength during variable selection even when the coefficient values differ markedly between tasks. We express our modeling framework as a Mixed-Integer Program, and propose efficient and scalable algorithms based on block coordinate descent and combinatorial local search. We show our estimator achieves statistically optimal prediction rates. Importantly, our theory characterizes how our estimator leverages the shared support information across tasks to achieve better variable selection performance. We evaluate the performance of our method in simulations and two biology applications. Our proposed approaches outperform other sparse MTL methods in variable selection and prediction accuracy. Interestingly, penalties that shrink the supports together often outperform penalties that shrink the coefficient values together. We will release an R package implementing our methods.

Multi-Study Boosting: Theoretical Considerations for Merging vs. Ensembling

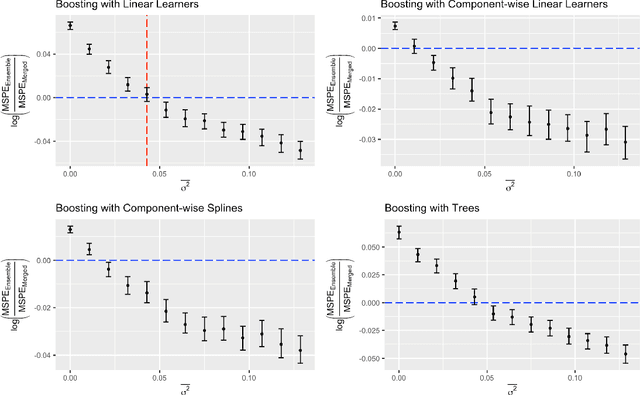
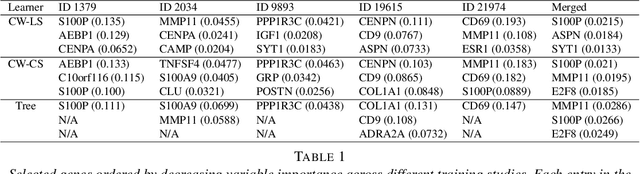
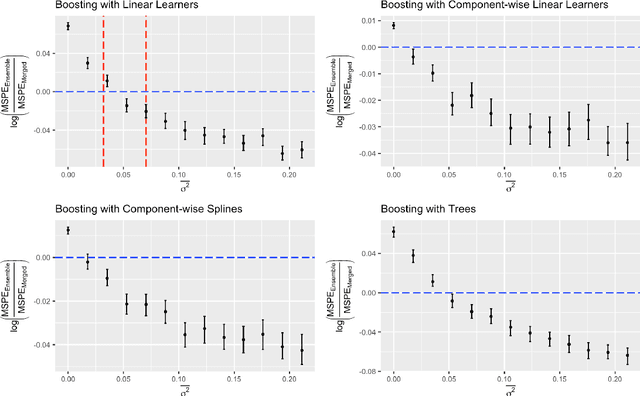
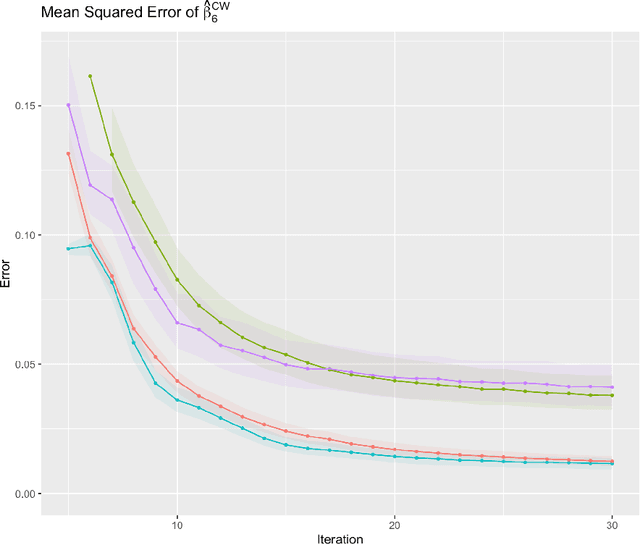
Cross-study replicability is a powerful model evaluation criterion that emphasizes generalizability of predictions. When training cross-study replicable prediction models, it is critical to decide between merging and treating the studies separately. We study boosting algorithms in the presence of potential heterogeneity in predictor-outcome relationships across studies and compare two multi-study learning strategies: 1) merging all the studies and training a single model, and 2) multi-study ensembling, which involves training a separate model on each study and ensembling the resulting predictions. In the regression setting, we provide theoretical guidelines based on an analytical transition point to determine whether it is more beneficial to merge or to ensemble for boosting with linear learners. In addition, we characterize a bias-variance decomposition of estimation error for boosting with component-wise linear learners. We verify the theoretical transition point result in simulation and illustrate how it can guide the decision on merging vs. ensembling in an application to breast cancer gene expression data.

Optimal Ensemble Construction for Multi-Study Prediction with Applications to COVID-19 Excess Mortality Estimation

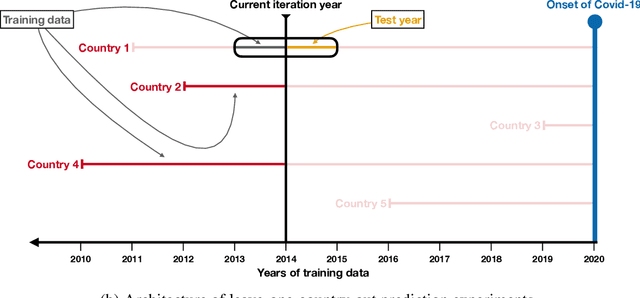
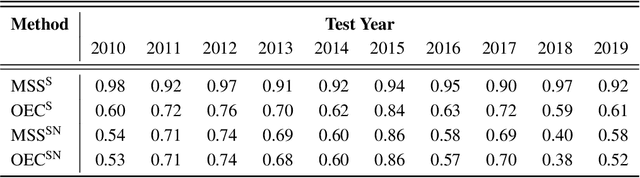
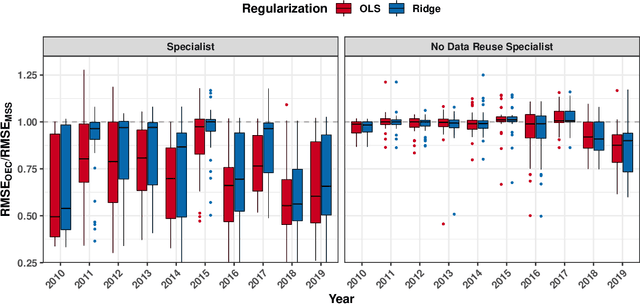
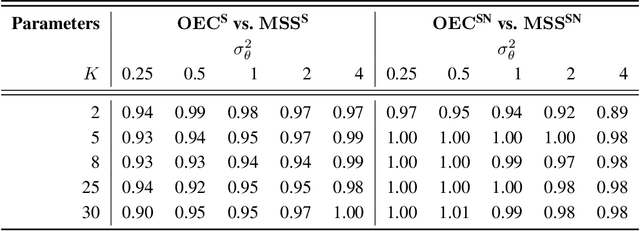
It is increasingly common to encounter prediction tasks in the biomedical sciences for which multiple datasets are available for model training. Common approaches such as pooling datasets and applying standard statistical learning methods can result in poor out-of-study prediction performance when datasets are heterogeneous. Theoretical and applied work has shown $\textit{multi-study ensembling}$ to be a viable alternative that leverages the variability across datasets in a manner that promotes model generalizability. Multi-study ensembling uses a two-stage $\textit{stacking}$ strategy which fits study-specific models and estimates ensemble weights separately. This approach ignores, however, the ensemble properties at the model-fitting stage, potentially resulting in a loss of efficiency. We therefore propose $\textit{optimal ensemble construction}$, an $\textit{all-in-one}$ approach to multi-study stacking whereby we jointly estimate ensemble weights as well as parameters associated with each study-specific model. We prove that limiting cases of our approach yield existing methods such as multi-study stacking and pooling datasets before model fitting. We propose an efficient block coordinate descent algorithm to optimize the proposed loss function. We compare our approach to standard methods by applying it to a multi-country COVID-19 dataset for baseline mortality prediction. We show that when little data is available for a country before the onset of the pandemic, leveraging data from other countries can substantially improve prediction accuracy. Importantly, our approach outperforms multi-study stacking and other standard methods in this application. We further characterize the method's performance in simulations. Our method remains competitive with or outperforms multi-study stacking and other earlier methods across a range of between-study heterogeneity levels.

Prediction of Hereditary Cancers Using Neural Networks

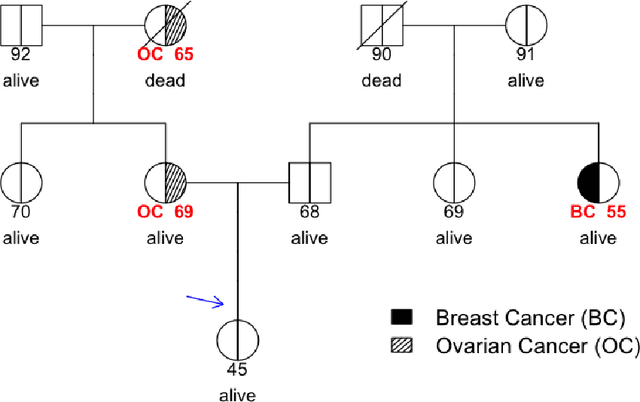
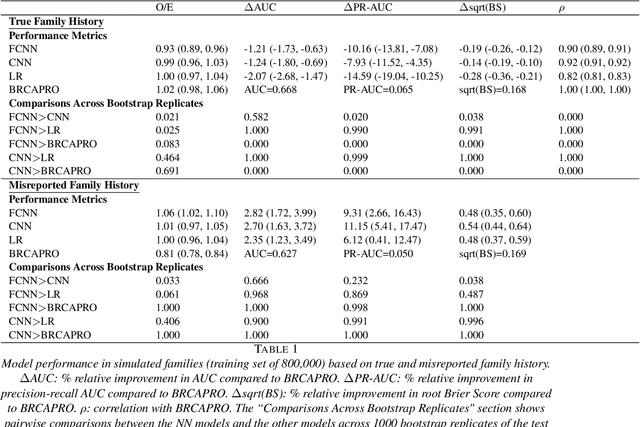
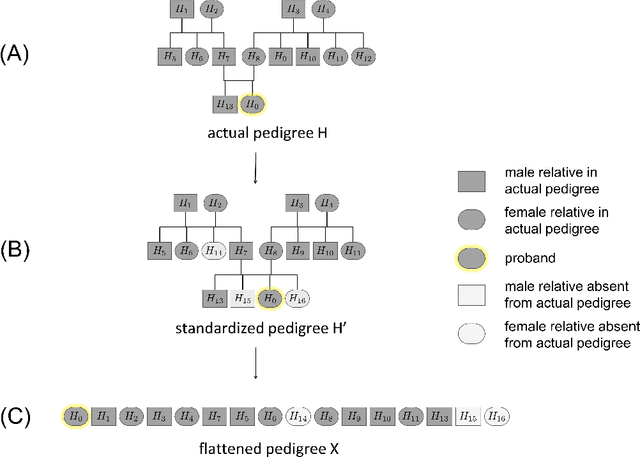
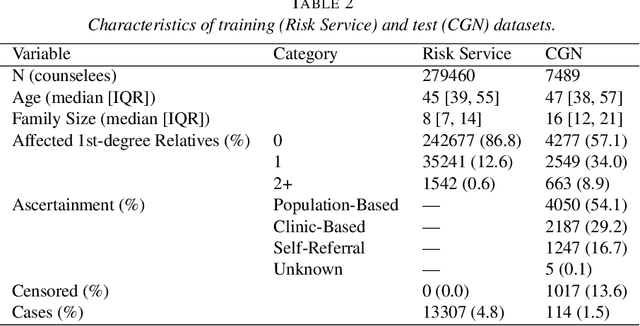
Family history is a major risk factor for many types of cancer. Mendelian risk prediction models translate family histories into cancer risk predictions based on knowledge of cancer susceptibility genes. These models are widely used in clinical practice to help identify high-risk individuals. Mendelian models leverage the entire family history, but they rely on many assumptions about cancer susceptibility genes that are either unrealistic or challenging to validate due to low mutation prevalence. Training more flexible models, such as neural networks, on large databases of pedigrees can potentially lead to accuracy gains. In this paper, we develop a framework to apply neural networks to family history data and investigate their ability to learn inherited susceptibility to cancer. While there is an extensive literature on neural networks and their state-of-the-art performance in many tasks, there is little work applying them to family history data. We propose adaptations of fully-connected neural networks and convolutional neural networks to pedigrees. In data simulated under Mendelian inheritance, we demonstrate that our proposed neural network models are able to achieve nearly optimal prediction performance. Moreover, when the observed family history includes misreported cancer diagnoses, neural networks are able to outperform the Mendelian BRCAPRO model embedding the correct inheritance laws. Using a large dataset of over 200,000 family histories, the Risk Service cohort, we train prediction models for future risk of breast cancer. We validate the models using data from the Cancer Genetics Network.

Cross-Cluster Weighted Forests

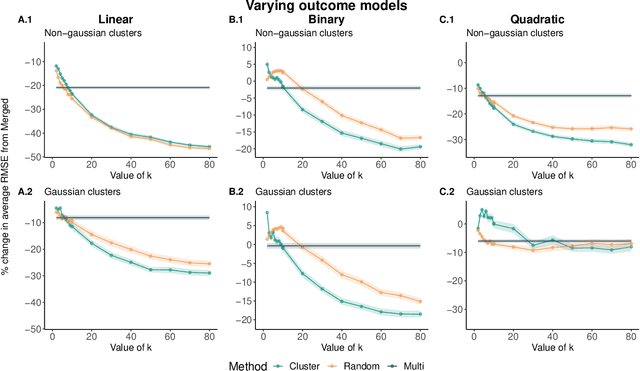
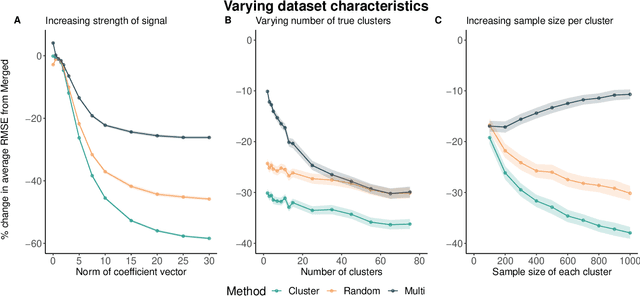
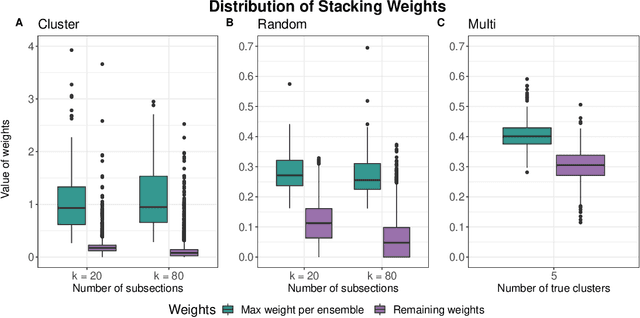
Adapting machine learning algorithms to better handle the presence of natural clustering or batch effects within training datasets is imperative across a wide variety of biological applications. This article considers the effect of ensembling Random Forest learners trained on clusters within a single dataset with heterogeneity in the distribution of the features. We find that constructing ensembles of forests trained on clusters determined by algorithms such as k-means results in significant improvements in accuracy and generalizability over the traditional Random Forest algorithm. We denote our novel approach as the Cross-Cluster Weighted Forest, and examine its robustness to various data-generating scenarios and outcome models. Furthermore, we explore the influence of the data-partitioning and ensemble weighting strategies on conferring the benefits of our method over the existing paradigm. Finally, we apply our approach to cancer molecular profiling and gene expression datasets that are naturally divisible into clusters and illustrate that our approach outperforms classic Random Forest. Code and supplementary material are available at https://github.com/m-ramchandran/cross-cluster.

Extending Models Via Gradient Boosting: An Application to Mendelian Models

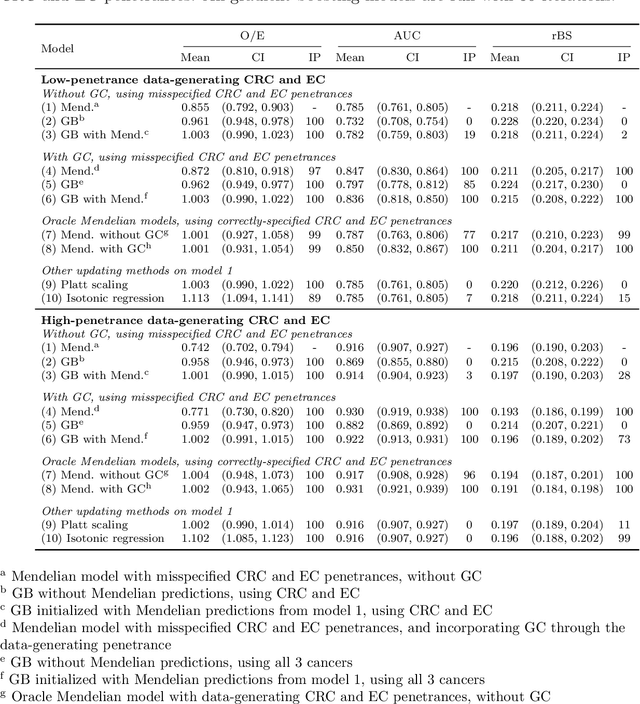
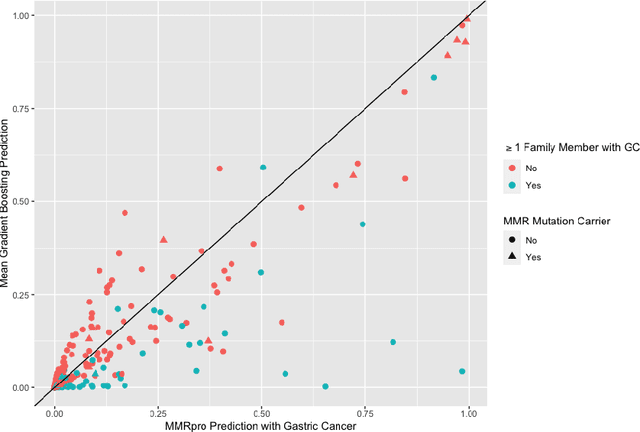
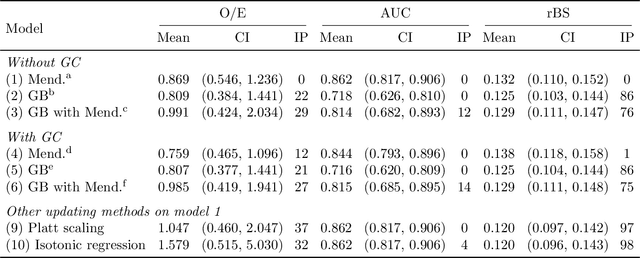
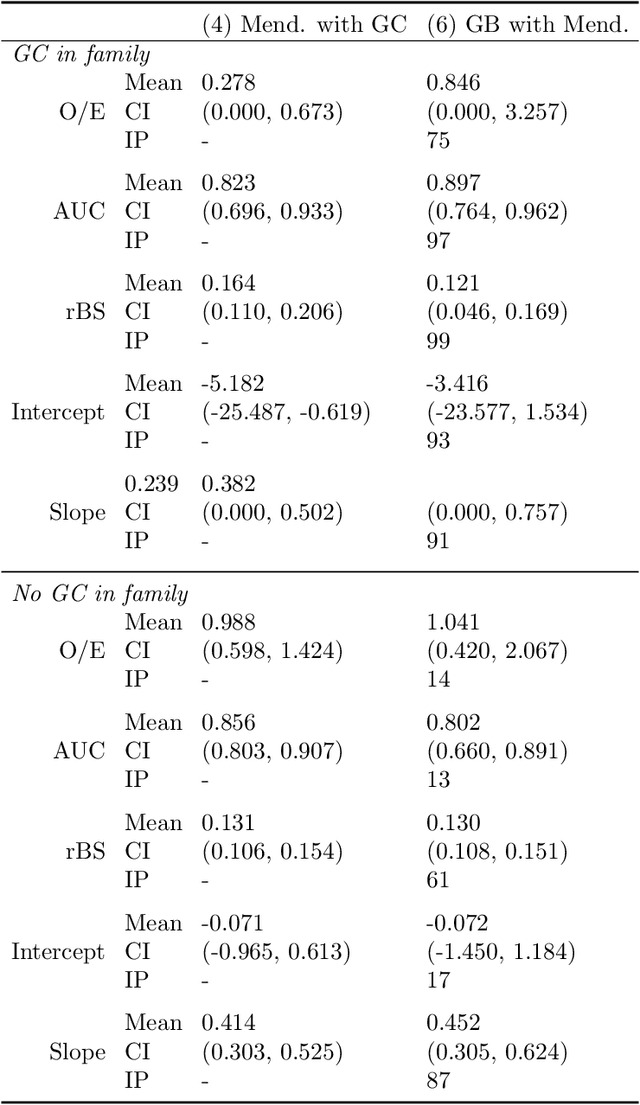
Improving existing widely-adopted prediction models is often a more efficient and robust way towards progress than training new models from scratch. Existing models may (a) incorporate complex mechanistic knowledge, (b) leverage proprietary information and, (c) have surmounted barriers to adoption. Compared to model training, model improvement and modification receive little attention. In this paper we propose a general approach to model improvement: we combine gradient boosting with any previously developed model to improve model performance while retaining important existing characteristics. To exemplify, we consider the context of Mendelian models, which estimate the probability of carrying genetic mutations that confer susceptibility to disease by using family pedigrees and health histories of family members. Via simulations we show that integration of gradient boosting with an existing Mendelian model can produce an improved model that outperforms both that model and the model built using gradient boosting alone. We illustrate the approach on genetic testing data from the USC-Stanford Cancer Genetics Hereditary Cancer Panel (HCP) study.

Representation via Representations: Domain Generalization via Adversarially Learned Invariant Representations

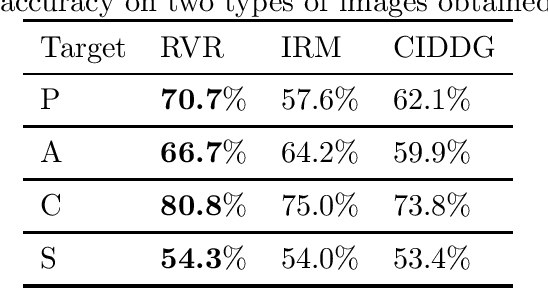
We investigate the power of censoring techniques, first developed for learning {\em fair representations}, to address domain generalization. We examine {\em adversarial} censoring techniques for learning invariant representations from multiple "studies" (or domains), where each study is drawn according to a distribution on domains. The mapping is used at test time to classify instances from a new domain. In many contexts, such as medical forecasting, domain generalization from studies in populous areas (where data are plentiful), to geographically remote populations (for which no training data exist) provides fairness of a different flavor, not anticipated in previous work on algorithmic fairness. We study an adversarial loss function for $k$ domains and precisely characterize its limiting behavior as $k$ grows, formalizing and proving the intuition, backed by experiments, that observing data from a larger number of domains helps. The limiting results are accompanied by non-asymptotic learning-theoretic bounds. Furthermore, we obtain sufficient conditions for good worst-case prediction performance of our algorithm on previously unseen domains. Finally, we decompose our mappings into two components and provide a complete characterization of invariance in terms of this decomposition. To our knowledge, our results provide the first formal guarantees of these kinds for adversarial invariant domain generalization.