Prediction of Hereditary Cancers Using Neural Networks

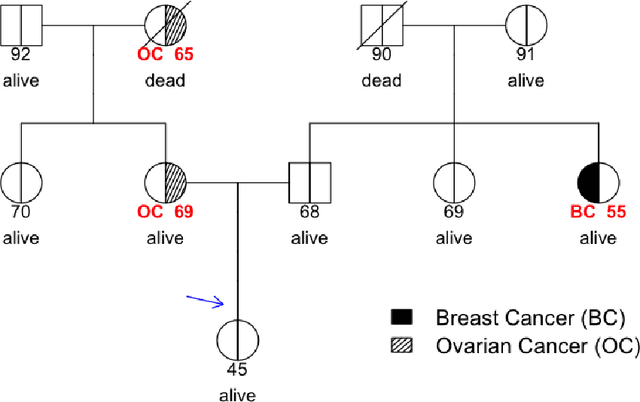
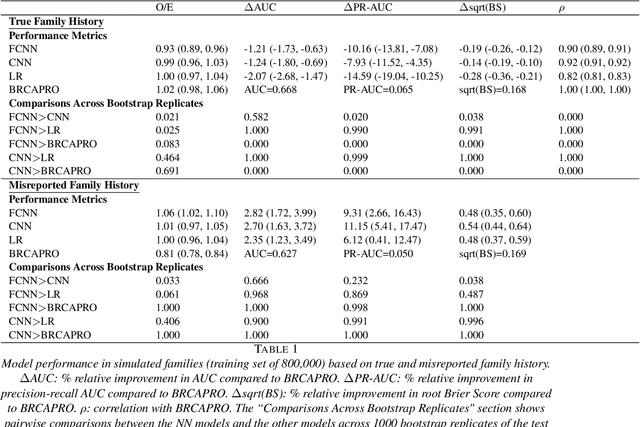
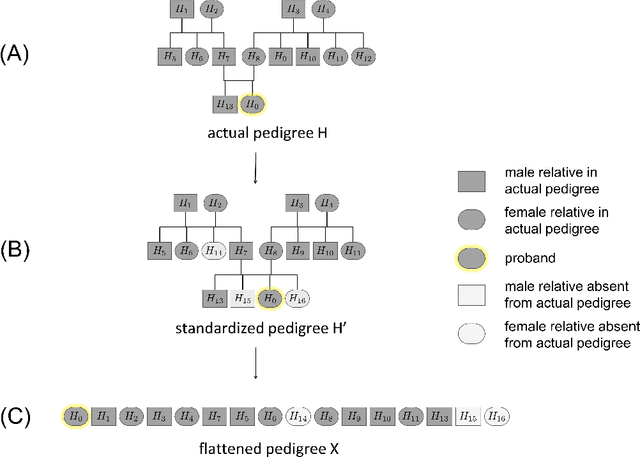
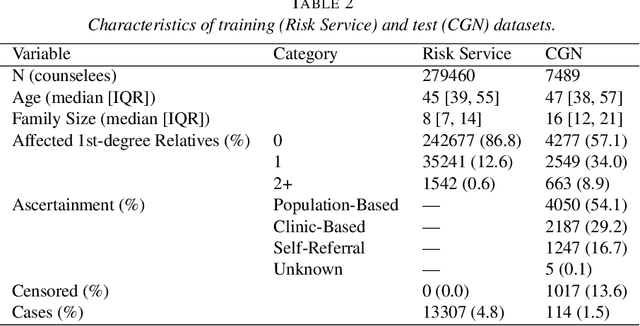
Family history is a major risk factor for many types of cancer. Mendelian risk prediction models translate family histories into cancer risk predictions based on knowledge of cancer susceptibility genes. These models are widely used in clinical practice to help identify high-risk individuals. Mendelian models leverage the entire family history, but they rely on many assumptions about cancer susceptibility genes that are either unrealistic or challenging to validate due to low mutation prevalence. Training more flexible models, such as neural networks, on large databases of pedigrees can potentially lead to accuracy gains. In this paper, we develop a framework to apply neural networks to family history data and investigate their ability to learn inherited susceptibility to cancer. While there is an extensive literature on neural networks and their state-of-the-art performance in many tasks, there is little work applying them to family history data. We propose adaptations of fully-connected neural networks and convolutional neural networks to pedigrees. In data simulated under Mendelian inheritance, we demonstrate that our proposed neural network models are able to achieve nearly optimal prediction performance. Moreover, when the observed family history includes misreported cancer diagnoses, neural networks are able to outperform the Mendelian BRCAPRO model embedding the correct inheritance laws. Using a large dataset of over 200,000 family histories, the Risk Service cohort, we train prediction models for future risk of breast cancer. We validate the models using data from the Cancer Genetics Network.

Merging versus Ensembling in Multi-Study Machine Learning: Theoretical Insight from Random Effects

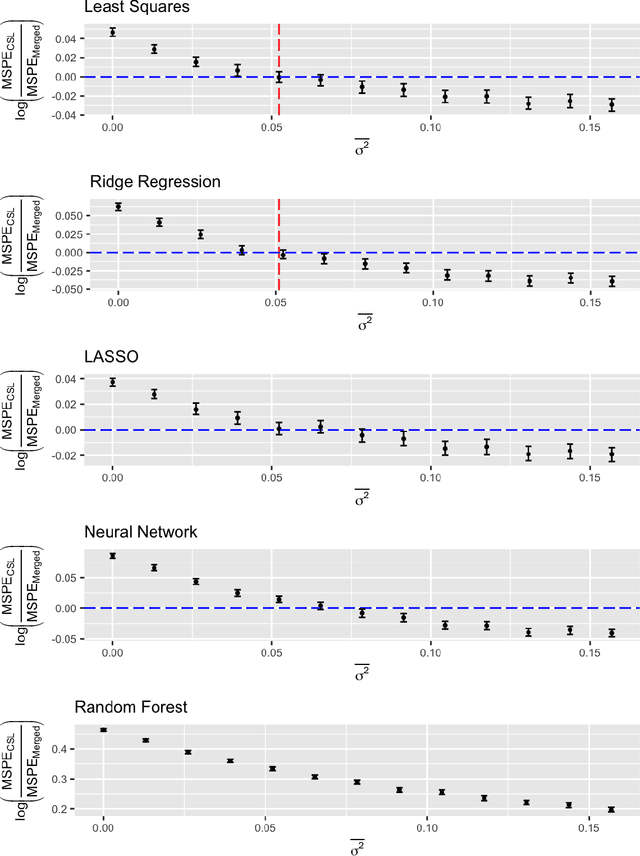
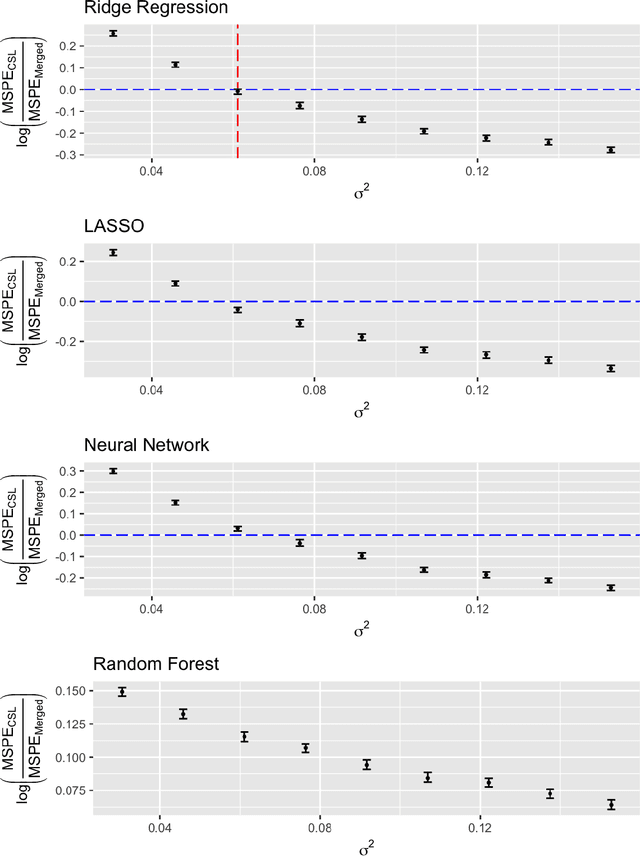
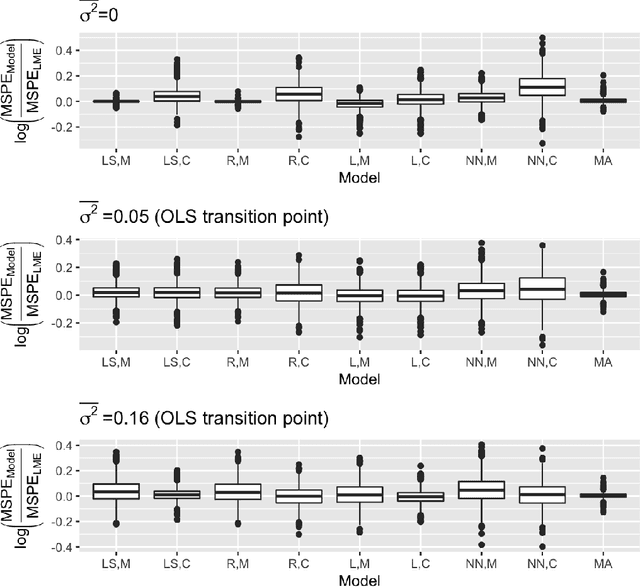
A critical decision point when training predictors using multiple studies is whether these studies should be combined or treated separately. We compare two multi-study learning approaches in the presence of potential heterogeneity in predictor-outcome relationships across datasets. We consider 1) merging all of the datasets and training a single learner, and 2) cross-study learning, which involves training a separate learner on each dataset and combining the resulting predictions. In a linear regression setting, we show analytically and confirm via simulation that merging yields lower prediction error than cross-study learning when the predictor-outcome relationships are relatively homogeneous across studies. However, as heterogeneity increases, there exists a transition point beyond which cross-study learning outperforms merging. We provide analytic expressions for the transition point in various scenarios and study asymptotic properties.