Multi-study R-learner for Heterogeneous Treatment Effect Estimation

Estimating heterogeneous treatment effects is crucial for informing personalized treatment strategies and policies. While multiple studies can improve the accuracy and generalizability of results, leveraging them for estimation is statistically challenging. Existing approaches often assume identical heterogeneous treatment effects across studies, but this may be violated due to various sources of between-study heterogeneity, including differences in study design, confounders, and sample characteristics. To this end, we propose a unifying framework for multi-study heterogeneous treatment effect estimation that is robust to between-study heterogeneity in the nuisance functions and treatment effects. Our approach, the multi-study R-learner, extends the R-learner to obtain principled statistical estimation with modern machine learning (ML) in the multi-study setting. The multi-study R-learner is easy to implement and flexible in its ability to incorporate ML for estimating heterogeneous treatment effects, nuisance functions, and membership probabilities, which borrow strength across heterogeneous studies. It achieves robustness in confounding adjustment through its loss function and can leverage both randomized controlled trials and observational studies. We provide asymptotic guarantees for the proposed method in the case of series estimation and illustrate using real cancer data that it has the lowest estimation error compared to existing approaches in the presence of between-study heterogeneity.

Multi-Study Boosting: Theoretical Considerations for Merging vs. Ensembling

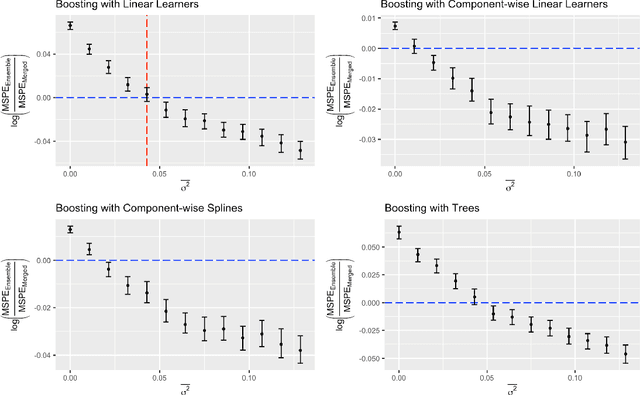
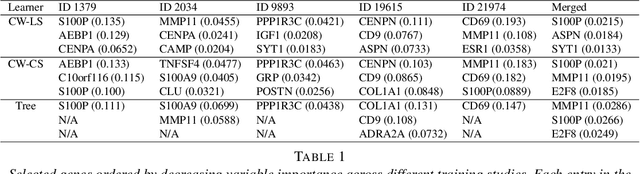
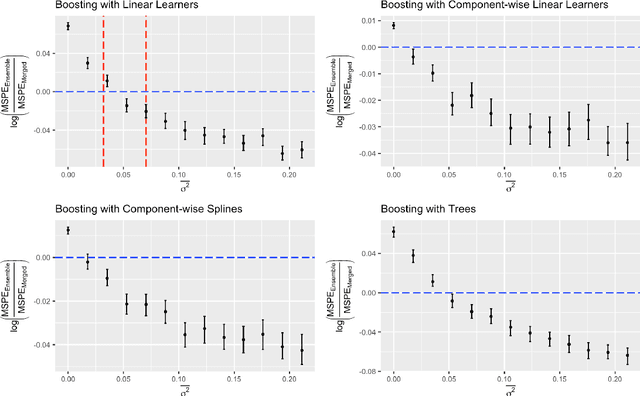
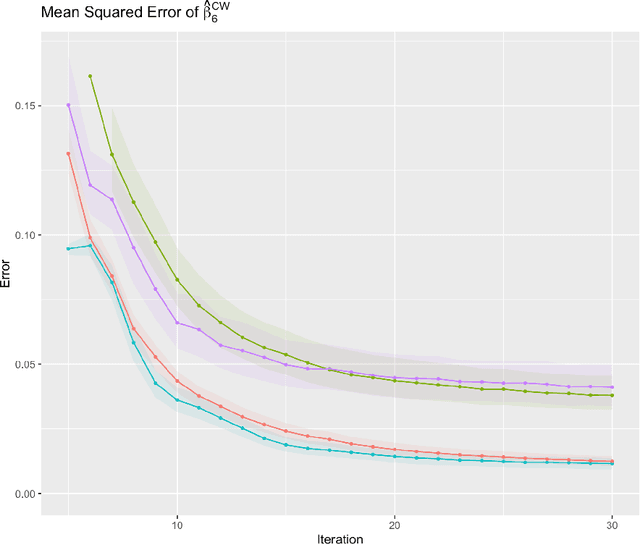
Cross-study replicability is a powerful model evaluation criterion that emphasizes generalizability of predictions. When training cross-study replicable prediction models, it is critical to decide between merging and treating the studies separately. We study boosting algorithms in the presence of potential heterogeneity in predictor-outcome relationships across studies and compare two multi-study learning strategies: 1) merging all the studies and training a single model, and 2) multi-study ensembling, which involves training a separate model on each study and ensembling the resulting predictions. In the regression setting, we provide theoretical guidelines based on an analytical transition point to determine whether it is more beneficial to merge or to ensemble for boosting with linear learners. In addition, we characterize a bias-variance decomposition of estimation error for boosting with component-wise linear learners. We verify the theoretical transition point result in simulation and illustrate how it can guide the decision on merging vs. ensembling in an application to breast cancer gene expression data.

Representation via Representations: Domain Generalization via Adversarially Learned Invariant Representations

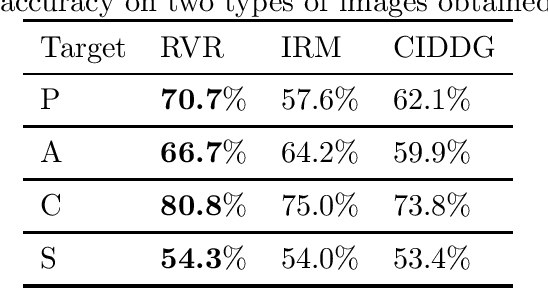
We investigate the power of censoring techniques, first developed for learning {\em fair representations}, to address domain generalization. We examine {\em adversarial} censoring techniques for learning invariant representations from multiple "studies" (or domains), where each study is drawn according to a distribution on domains. The mapping is used at test time to classify instances from a new domain. In many contexts, such as medical forecasting, domain generalization from studies in populous areas (where data are plentiful), to geographically remote populations (for which no training data exist) provides fairness of a different flavor, not anticipated in previous work on algorithmic fairness. We study an adversarial loss function for $k$ domains and precisely characterize its limiting behavior as $k$ grows, formalizing and proving the intuition, backed by experiments, that observing data from a larger number of domains helps. The limiting results are accompanied by non-asymptotic learning-theoretic bounds. Furthermore, we obtain sufficient conditions for good worst-case prediction performance of our algorithm on previously unseen domains. Finally, we decompose our mappings into two components and provide a complete characterization of invariance in terms of this decomposition. To our knowledge, our results provide the first formal guarantees of these kinds for adversarial invariant domain generalization.

Merging versus Ensembling in Multi-Study Machine Learning: Theoretical Insight from Random Effects

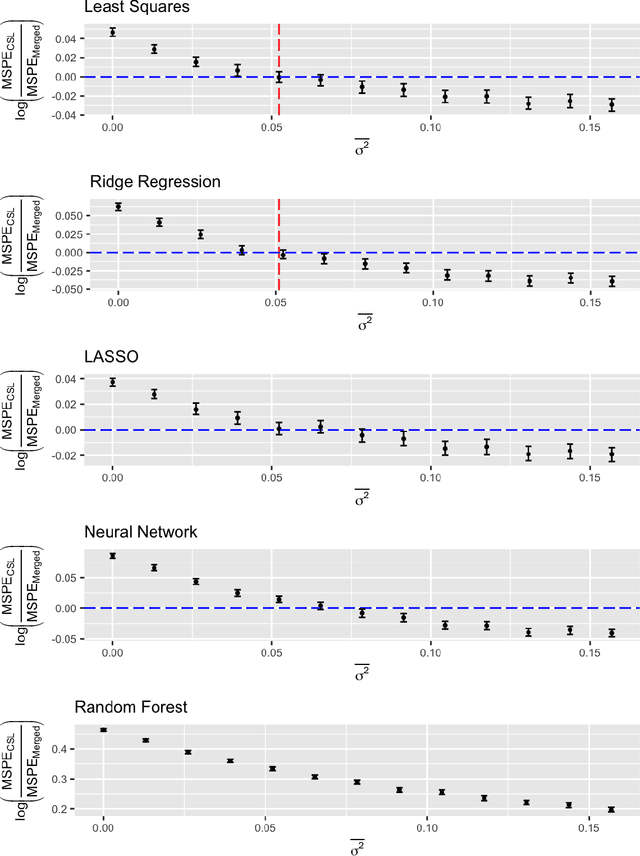
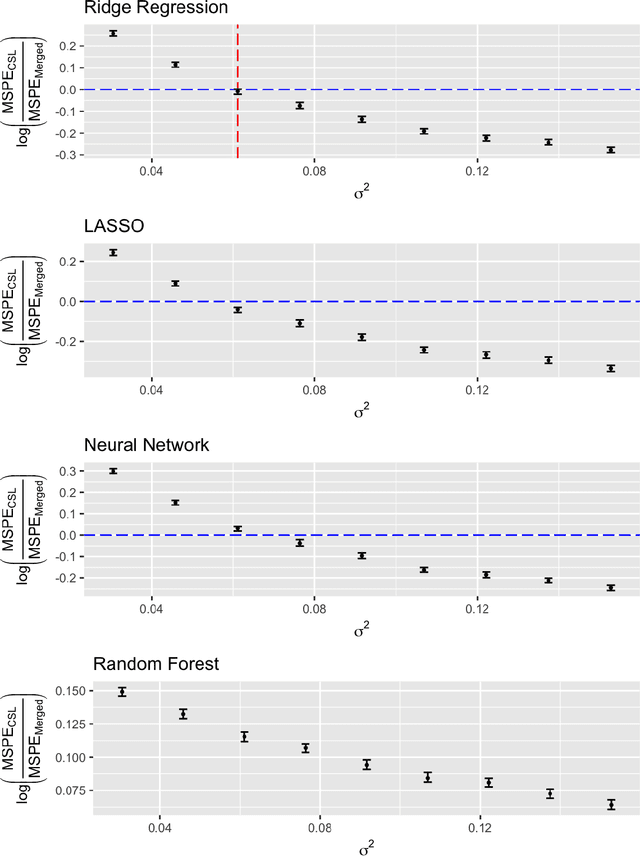
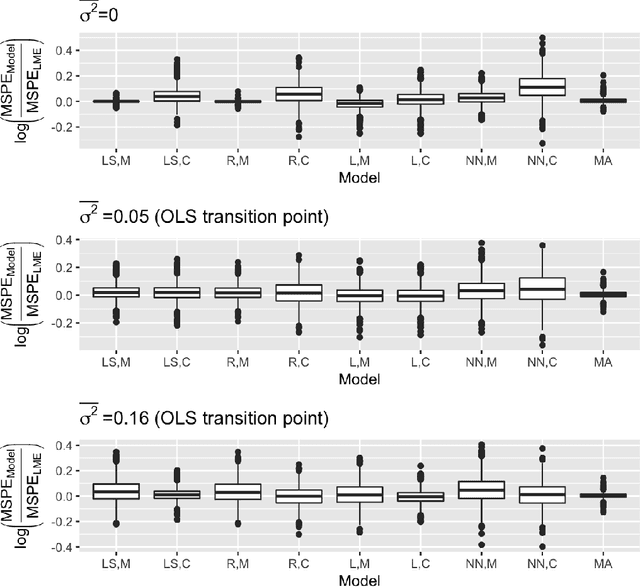
A critical decision point when training predictors using multiple studies is whether these studies should be combined or treated separately. We compare two multi-study learning approaches in the presence of potential heterogeneity in predictor-outcome relationships across datasets. We consider 1) merging all of the datasets and training a single learner, and 2) cross-study learning, which involves training a separate learner on each dataset and combining the resulting predictions. In a linear regression setting, we show analytically and confirm via simulation that merging yields lower prediction error than cross-study learning when the predictor-outcome relationships are relatively homogeneous across studies. However, as heterogeneity increases, there exists a transition point beyond which cross-study learning outperforms merging. We provide analytic expressions for the transition point in various scenarios and study asymptotic properties.