From Fairness to Infinity: Outcome-Indistinguishable (Omni)Prediction in Evolving Graphs

Professional networks provide invaluable entree to opportunity through referrals and introductions. A rich literature shows they also serve to entrench and even exacerbate a status quo of privilege and disadvantage. Hiring platforms, equipped with the ability to nudge link formation, provide a tantalizing opening for beneficial structural change. We anticipate that key to this prospect will be the ability to estimate the likelihood of edge formation in an evolving graph. Outcome-indistinguishable prediction algorithms ensure that the modeled world is indistinguishable from the real world by a family of statistical tests. Omnipredictors ensure that predictions can be post-processed to yield loss minimization competitive with respect to a benchmark class of predictors for many losses simultaneously, with appropriate post-processing. We begin by observing that, by combining a slightly modified form of the online K29 star algorithm of Vovk (2007) with basic facts from the theory of reproducing kernel Hilbert spaces, one can derive simple and efficient online algorithms satisfying outcome indistinguishability and omniprediction, with guarantees that improve upon, or are complementary to, those currently known. This is of independent interest. We apply these techniques to evolving graphs, obtaining online outcome-indistinguishable omnipredictors for rich -- possibly infinite -- sets of distinguishers that capture properties of pairs of nodes, and their neighborhoods. This yields, inter alia, multicalibrated predictions of edge formation with respect to pairs of demographic groups, and the ability to simultaneously optimize loss as measured by a variety of social welfare functions.

Differentially Private Learning Beyond the Classical Dimensionality Regime

We initiate the study of differentially private learning in the proportional dimensionality regime, in which the number of data samples $n$ and problem dimension $d$ approach infinity at rates proportional to one another, meaning that $d / n \to \delta$ as $n \to \infty$ for an arbitrary, given constant $\delta \in (0, \infty)$. This setting is significantly more challenging than that of all prior theoretical work in high-dimensional differentially private learning, which, despite the name, has assumed that $\delta = 0$ or is sufficiently small for problems of sample complexity $O(d)$, a regime typically considered "low-dimensional" or "classical" by modern standards in high-dimensional statistics. We provide sharp theoretical estimates of the error of several well-studied differentially private algorithms for robust linear regression and logistic regression, including output perturbation, objective perturbation, and noisy stochastic gradient descent, in the proportional dimensionality regime. The $1 + o(1)$ factor precision of our error estimates enables a far more nuanced understanding of the price of privacy of these algorithms than that afforded by existing, coarser analyses, which are essentially vacuous in the regime we consider. We incorporate several probabilistic tools that have not previously been used to analyze differentially private learning algorithms, such as a modern Gaussian comparison inequality and recent universality laws with origins in statistical physics.

Set-Based Prompting: Provably Solving the Language Model Order Dependency Problem

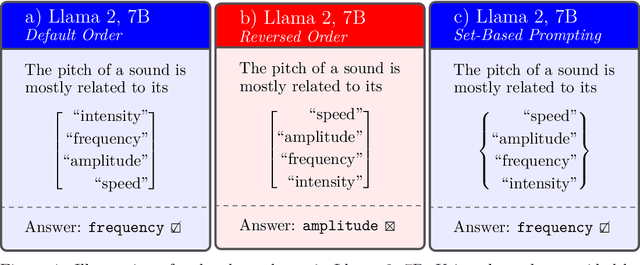
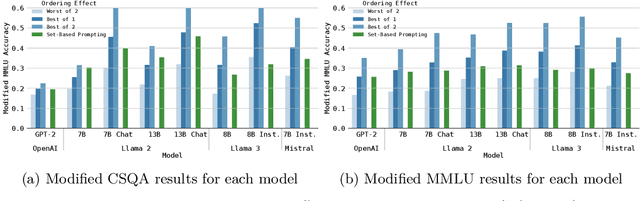
The development of generative language models that can create long and coherent textual outputs via autoregression has lead to a proliferation of uses and a corresponding sweep of analyses as researches work to determine the limitations of this new paradigm. Unlike humans, these 'Large Language Models' (LLMs) are highly sensitive to small changes in their inputs, leading to unwanted inconsistency in their behavior. One problematic inconsistency when LLMs are used to answer multiple-choice questions or analyze multiple inputs is order dependency: the output of an LLM can (and often does) change significantly when sub-sequences are swapped, despite both orderings being semantically identical. In this paper we present Set-Based Prompting, a technique that guarantees the output of an LLM will not have order dependence on a specified set of sub-sequences. We show that this method provably eliminates order dependency, and that it can be applied to any transformer-based LLM to enable text generation that is unaffected by re-orderings. Delving into the implications of our method, we show that, despite our inputs being out of distribution, the impact on expected accuracy is small, where the expectation is over the order of uniformly chosen shuffling of the candidate responses, and usually significantly less in practice. Thus, Set-Based Prompting can be used as a 'dropped-in' method on fully trained models. Finally, we discuss how our method's success suggests that other strong guarantees can be obtained on LLM performance via modifying the input representations.

HappyMap: A Generalized Multi-calibration Method

Multi-calibration is a powerful and evolving concept originating in the field of algorithmic fairness. For a predictor $f$ that estimates the outcome $y$ given covariates $x$, and for a function class $\mathcal{C}$, multi-calibration requires that the predictor $f(x)$ and outcome $y$ are indistinguishable under the class of auditors in $\mathcal{C}$. Fairness is captured by incorporating demographic subgroups into the class of functions~$\mathcal{C}$. Recent work has shown that, by enriching the class $\mathcal{C}$ to incorporate appropriate propensity re-weighting functions, multi-calibration also yields target-independent learning, wherein a model trained on a source domain performs well on unseen, future, target domains(approximately) captured by the re-weightings. Formally, multi-calibration with respect to $\mathcal{C}$ bounds $\big|\mathbb{E}_{(x,y)\sim \mathcal{D}}[c(f(x),x)\cdot(f(x)-y)]\big|$ for all $c \in \mathcal{C}$. In this work, we view the term $(f(x)-y)$ as just one specific mapping, and explore the power of an enriched class of mappings. We propose \textit{HappyMap}, a generalization of multi-calibration, which yields a wide range of new applications, including a new fairness notion for uncertainty quantification (conformal prediction), a novel technique for conformal prediction under covariate shift, and a different approach to analyzing missing data, while also yielding a unified understanding of several existing seemingly disparate algorithmic fairness notions and target-independent learning approaches. We give a single \textit{HappyMap} meta-algorithm that captures all these results, together with a sufficiency condition for its success.

New Insights into Multi-Calibration

We identify a novel connection between the recent literature on multi-group fairness for prediction algorithms and well-established notions of graph regularity from extremal graph theory. We frame our investigation using new, statistical distance-based variants of multi-calibration that are closely related to the concept of outcome indistinguishability. Adopting this perspective leads us naturally not only to our graph theoretic results, but also to new multi-calibration algorithms with improved complexity in certain parameter regimes, and to a generalization of a state-of-the-art result on omniprediction. Along the way, we also unify several prior algorithms for achieving multi-group fairness, as well as their analyses, through the lens of no-regret learning.

Confidence-Ranked Reconstruction of Census Microdata from Published Statistics

A reconstruction attack on a private dataset $D$ takes as input some publicly accessible information about the dataset and produces a list of candidate elements of $D$. We introduce a new class of data reconstruction attacks based on randomized methods for non-convex optimization. We empirically demonstrate that our attacks can not only reconstruct full rows of $D$ from aggregate query statistics $Q(D)\in \mathbb{R}^m$, but can do so in a way that reliably ranks reconstructed rows by their odds of appearing in the private data, providing a signature that could be used for prioritizing reconstructed rows for further actions such as identify theft or hate crime. We also design a sequence of baselines for evaluating reconstruction attacks. Our attacks significantly outperform those that are based only on access to a public distribution or population from which the private dataset $D$ was sampled, demonstrating that they are exploiting information in the aggregate statistics $Q(D)$, and not simply the overall structure of the distribution. In other words, the queries $Q(D)$ are permitting reconstruction of elements of this dataset, not the distribution from which $D$ was drawn. These findings are established both on 2010 U.S. decennial Census data and queries and Census-derived American Community Survey datasets. Taken together, our methods and experiments illustrate the risks in releasing numerically precise aggregate statistics of a large dataset, and provide further motivation for the careful application of provably private techniques such as differential privacy.

Improved Generalization Guarantees in Restricted Data Models

Differential privacy is known to protect against threats to validity incurred due to adaptive, or exploratory, data analysis -- even when the analyst adversarially searches for a statistical estimate that diverges from the true value of the quantity of interest on the underlying population. The cost of this protection is the accuracy loss incurred by differential privacy. In this work, inspired by standard models in the genomics literature, we consider data models in which individuals are represented by a sequence of attributes with the property that where distant attributes are only weakly correlated. We show that, under this assumption, it is possible to "re-use" privacy budget on different portions of the data, significantly improving accuracy without increasing the risk of overfitting.

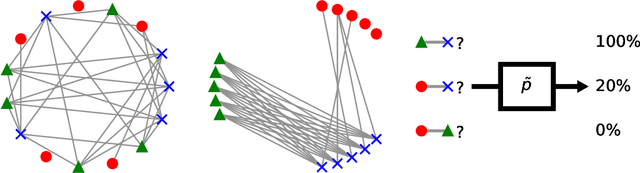
Scaffolding Sets

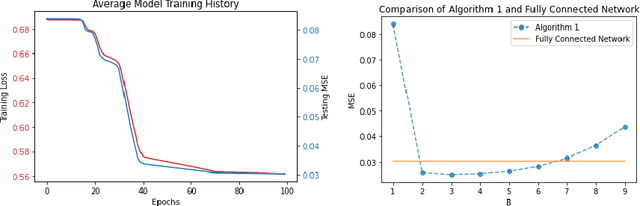
Predictors map individual instances in a population to the interval $[0,1]$. For a collection $\mathcal C$ of subsets of a population, a predictor is multi-calibrated with respect to $\mathcal C$ if it is simultaneously calibrated on each set in $\mathcal C$. We initiate the study of the construction of scaffolding sets, a small collection $\mathcal S$ of sets with the property that multi-calibration with respect to $\mathcal S$ ensures correctness, and not just calibration, of the predictor. Our approach is inspired by the folk wisdom that the intermediate layers of a neural net learn a highly structured and useful data representation.

Outcome Indistinguishability

Prediction algorithms assign numbers to individuals that are popularly understood as individual "probabilities" -- what is the probability of 5-year survival after cancer diagnosis? -- and which increasingly form the basis for life-altering decisions. Drawing on an understanding of computational indistinguishability developed in complexity theory and cryptography, we introduce Outcome Indistinguishability. Predictors that are Outcome Indistinguishable yield a generative model for outcomes that cannot be efficiently refuted on the basis of the real-life observations produced by Nature. We investigate a hierarchy of Outcome Indistinguishability definitions, whose stringency increases with the degree to which distinguishers may access the predictor in question. Our findings reveal that Outcome Indistinguishability behaves qualitatively differently than previously studied notions of indistinguishability. First, we provide constructions at all levels of the hierarchy. Then, leveraging recently-developed machinery for proving average-case fine-grained hardness, we obtain lower bounds on the complexity of the more stringent forms of Outcome Indistinguishability. This hardness result provides the first scientific grounds for the political argument that, when inspecting algorithmic risk prediction instruments, auditors should be granted oracle access to the algorithm, not simply historical predictions.

Interpreting Robust Optimization via Adversarial Influence Functions

Robust optimization has been widely used in nowadays data science, especially in adversarial training. However, little research has been done to quantify how robust optimization changes the optimizers and the prediction losses comparing to standard training. In this paper, inspired by the influence function in robust statistics, we introduce the Adversarial Influence Function (AIF) as a tool to investigate the solution produced by robust optimization. The proposed AIF enjoys a closed-form and can be calculated efficiently. To illustrate the usage of AIF, we apply it to study model sensitivity -- a quantity defined to capture the change of prediction losses on the natural data after implementing robust optimization. We use AIF to analyze how model complexity and randomized smoothing affect the model sensitivity with respect to specific models. We further derive AIF for kernel regressions, with a particular application to neural tangent kernels, and experimentally demonstrate the effectiveness of the proposed AIF. Lastly, the theories of AIF will be extended to distributional robust optimization.