Scaffolding Sets
Paper and Code
Nov 17, 2021
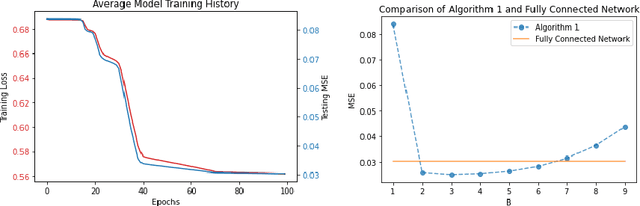

Predictors map individual instances in a population to the interval $[0,1]$. For a collection $\mathcal C$ of subsets of a population, a predictor is multi-calibrated with respect to $\mathcal C$ if it is simultaneously calibrated on each set in $\mathcal C$. We initiate the study of the construction of scaffolding sets, a small collection $\mathcal S$ of sets with the property that multi-calibration with respect to $\mathcal S$ ensures correctness, and not just calibration, of the predictor. Our approach is inspired by the folk wisdom that the intermediate layers of a neural net learn a highly structured and useful data representation.
* 32 pages, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge