Near-Optimal Algorithms for Omniprediction

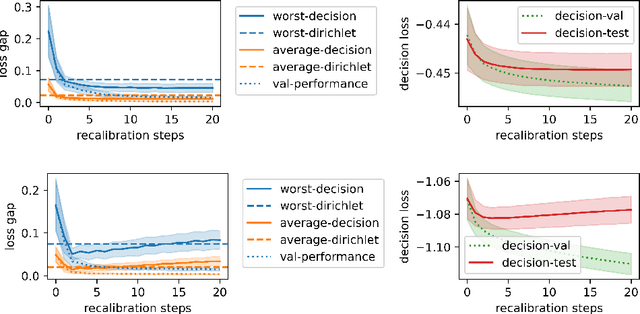
Omnipredictors are simple prediction functions that encode loss-minimizing predictions with respect to a hypothesis class $\mathcal{H}$, simultaneously for every loss function within a class of losses $\mathcal{L}$. In this work, we give near-optimal learning algorithms for omniprediction, in both the online and offline settings. To begin, we give an oracle-efficient online learning algorithm that acheives $(\mathcal{L},\mathcal{H})$-omniprediction with $\tilde{O}(\sqrt{T \log |\mathcal{H}|})$ regret for any class of Lipschitz loss functions $\mathcal{L} \subseteq \mathcal{L}_\mathrm{Lip}$. Quite surprisingly, this regret bound matches the optimal regret for \emph{minimization of a single loss function} (up to a $\sqrt{\log(T)}$ factor). Given this online algorithm, we develop an online-to-offline conversion that achieves near-optimal complexity across a number of measures. In particular, for all bounded loss functions within the class of Bounded Variation losses $\mathcal{L}_\mathrm{BV}$ (which include all convex, all Lipschitz, and all proper losses) and any (possibly-infinite) $\mathcal{H}$, we obtain an offline learning algorithm that, leveraging an (offline) ERM oracle and $m$ samples from $\mathcal{D}$, returns an efficient $(\mathcal{L}_{\mathrm{BV}},\mathcal{H},\varepsilon(m))$-omnipredictor for $\varepsilon(m)$ scaling near-linearly in the Rademacher complexity of $\mathrm{Th} \circ \mathcal{H}$.

Characterizing notions of omniprediction via multicalibration

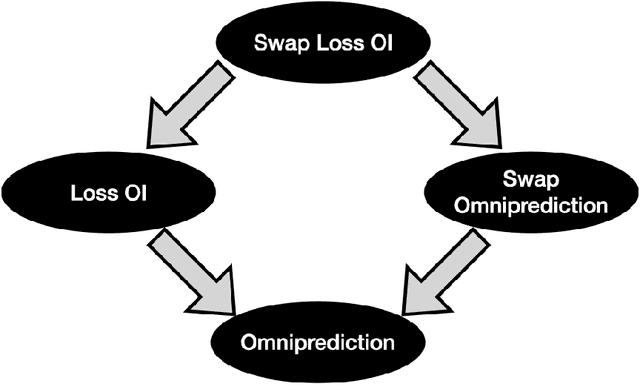
A recent line of work shows that notions of multigroup fairness imply surprisingly strong notions of omniprediction: loss minimization guarantees that apply not just for a specific loss function, but for any loss belonging to a large family of losses. While prior work has derived various notions of omniprediction from multigroup fairness guarantees of varying strength, it was unknown whether the connection goes in both directions. In this work, we answer this question in the affirmative, establishing equivalences between notions of multicalibration and omniprediction. The new definitions that hold the key to this equivalence are new notions of swap omniprediction, which are inspired by swap regret in online learning. We show that these can be characterized exactly by a strengthening of multicalibration that we refer to as swap multicalibration. One can go from standard to swap multicalibration by a simple discretization; moreover all known algorithms for standard multicalibration in fact give swap multicalibration. In the context of omniprediction though, introducing the notion of swapping results in provably stronger notions, which require a predictor to minimize expected loss at least as well as an adaptive adversary who can choose both the loss function and hypothesis based on the value predicted by the predictor. Building on these characterizations, we paint a complete picture of the relationship between the various omniprediction notions in the literature by establishing implications and separations between them. Our work deepens our understanding of the connections between multigroup fairness, loss minimization and outcome indistinguishability and establishes new connections to classic notions in online learning.

Loss Minimization through the Lens of Outcome Indistinguishability

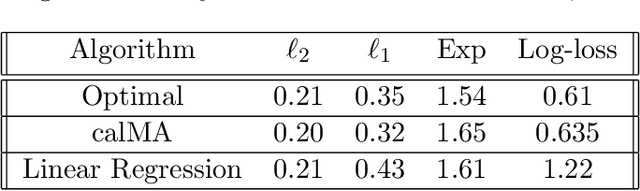
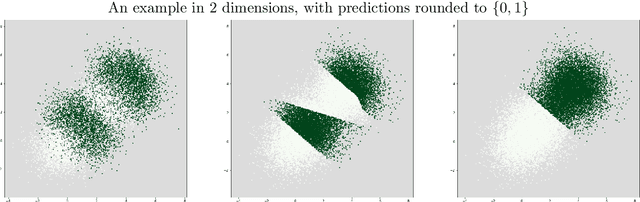
We present a new perspective on loss minimization and the recent notion of Omniprediction through the lens of Outcome Indistingusihability. For a collection of losses and hypothesis class, omniprediction requires that a predictor provide a loss-minimization guarantee simultaneously for every loss in the collection compared to the best (loss-specific) hypothesis in the class. We present a generic template to learn predictors satisfying a guarantee we call Loss Outcome Indistinguishability. For a set of statistical tests--based on a collection of losses and hypothesis class--a predictor is Loss OI if it is indistinguishable (according to the tests) from Nature's true probabilities over outcomes. By design, Loss OI implies omniprediction in a direct and intuitive manner. We simplify Loss OI further, decomposing it into a calibration condition plus multiaccuracy for a class of functions derived from the loss and hypothesis classes. By careful analysis of this class, we give efficient constructions of omnipredictors for interesting classes of loss functions, including non-convex losses. This decomposition highlights the utility of a new multi-group fairness notion that we call calibrated multiaccuracy, which lies in between multiaccuracy and multicalibration. We show that calibrated multiaccuracy implies Loss OI for the important set of convex losses arising from Generalized Linear Models, without requiring full multicalibration. For such losses, we show an equivalence between our computational notion of Loss OI and a geometric notion of indistinguishability, formulated as Pythagorean theorems in the associated Bregman divergence. We give an efficient algorithm for calibrated multiaccuracy with computational complexity comparable to that of multiaccuracy. In all, calibrated multiaccuracy offers an interesting tradeoff point between efficiency and generality in the omniprediction landscape.

Making Decisions under Outcome Performativity

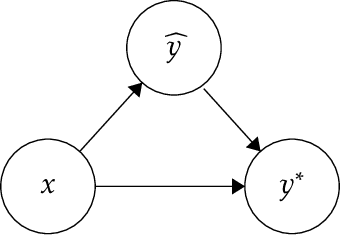
Decision-makers often act in response to data-driven predictions, with the goal of achieving favorable outcomes. In such settings, predictions don't passively forecast the future; instead, predictions actively shape the distribution of outcomes they are meant to predict. This performative prediction setting raises new challenges for learning "optimal" decision rules. In particular, existing solution concepts do not address the apparent tension between the goals of forecasting outcomes accurately and steering individuals to achieve desirable outcomes. To contend with this concern, we introduce a new optimality concept -- performative omniprediction -- adapted from the supervised (non-performative) learning setting. A performative omnipredictor is a single predictor that simultaneously encodes the optimal decision rule with respect to many possibly-competing objectives. Our main result demonstrates that efficient performative omnipredictors exist, under a natural restriction of performative prediction, which we call outcome performativity. On a technical level, our results follow by carefully generalizing the notion of outcome indistinguishability to the outcome performative setting. From an appropriate notion of Performative OI, we recover many consequences known to hold in the supervised setting, such as omniprediction and universal adaptability.

Backward baselines: Is your model predicting the past?

When does a machine learning model predict the future of individuals and when does it recite patterns that predate the individuals? In this work, we propose a distinction between these two pathways of prediction, supported by theoretical, empirical, and normative arguments. At the center of our proposal is a family of simple and efficient statistical tests, called backward baselines, that demonstrate if, and to which extent, a model recounts the past. Our statistical theory provides guidance for interpreting backward baselines, establishing equivalences between different baselines and familiar statistical concepts. Concretely, we derive a meaningful backward baseline for auditing a prediction system as a black box, given only background variables and the system's predictions. Empirically, we evaluate the framework on different prediction tasks derived from longitudinal panel surveys, demonstrating the ease and effectiveness of incorporating backward baselines into the practice of machine learning.

Planting Undetectable Backdoors in Machine Learning Models

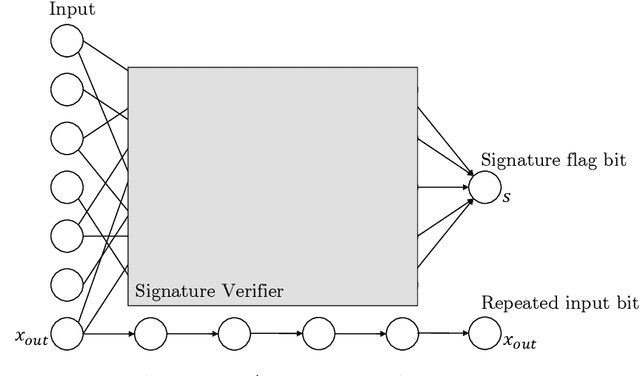
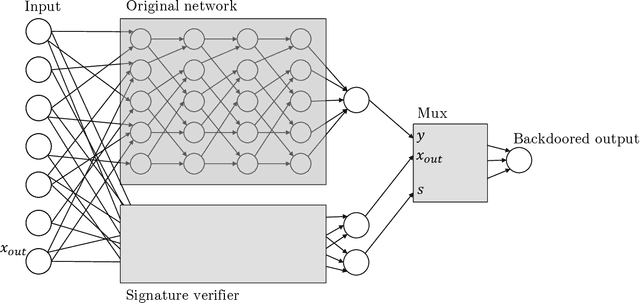
Given the computational cost and technical expertise required to train machine learning models, users may delegate the task of learning to a service provider. We show how a malicious learner can plant an undetectable backdoor into a classifier. On the surface, such a backdoored classifier behaves normally, but in reality, the learner maintains a mechanism for changing the classification of any input, with only a slight perturbation. Importantly, without the appropriate "backdoor key", the mechanism is hidden and cannot be detected by any computationally-bounded observer. We demonstrate two frameworks for planting undetectable backdoors, with incomparable guarantees. First, we show how to plant a backdoor in any model, using digital signature schemes. The construction guarantees that given black-box access to the original model and the backdoored version, it is computationally infeasible to find even a single input where they differ. This property implies that the backdoored model has generalization error comparable with the original model. Second, we demonstrate how to insert undetectable backdoors in models trained using the Random Fourier Features (RFF) learning paradigm or in Random ReLU networks. In this construction, undetectability holds against powerful white-box distinguishers: given a complete description of the network and the training data, no efficient distinguisher can guess whether the model is "clean" or contains a backdoor. Our construction of undetectable backdoors also sheds light on the related issue of robustness to adversarial examples. In particular, our construction can produce a classifier that is indistinguishable from an "adversarially robust" classifier, but where every input has an adversarial example! In summary, the existence of undetectable backdoors represent a significant theoretical roadblock to certifying adversarial robustness.

Low-Degree Multicalibration

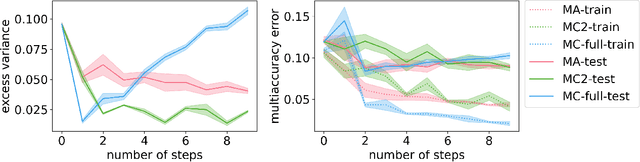
Introduced as a notion of algorithmic fairness, multicalibration has proved to be a powerful and versatile concept with implications far beyond its original intent. This stringent notion -- that predictions be well-calibrated across a rich class of intersecting subpopulations -- provides its strong guarantees at a cost: the computational and sample complexity of learning multicalibrated predictors are high, and grow exponentially with the number of class labels. In contrast, the relaxed notion of multiaccuracy can be achieved more efficiently, yet many of the most desirable properties of multicalibration cannot be guaranteed assuming multiaccuracy alone. This tension raises a key question: Can we learn predictors with multicalibration-style guarantees at a cost commensurate with multiaccuracy? In this work, we define and initiate the study of Low-Degree Multicalibration. Low-Degree Multicalibration defines a hierarchy of increasingly-powerful multi-group fairness notions that spans multiaccuracy and the original formulation of multicalibration at the extremes. Our main technical contribution demonstrates that key properties of multicalibration, related to fairness and accuracy, actually manifest as low-degree properties. Importantly, we show that low-degree multicalibration can be significantly more efficient than full multicalibration. In the multi-class setting, the sample complexity to achieve low-degree multicalibration improves exponentially (in the number of classes) over full multicalibration. Our work presents compelling evidence that low-degree multicalibration represents a sweet spot, pairing computational and sample efficiency with strong fairness and accuracy guarantees.

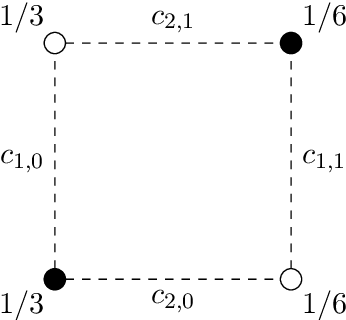
Calibrating Predictions to Decisions: A Novel Approach to Multi-Class Calibration

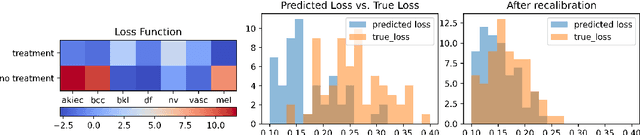
When facing uncertainty, decision-makers want predictions they can trust. A machine learning provider can convey confidence to decision-makers by guaranteeing their predictions are distribution calibrated -- amongst the inputs that receive a predicted class probabilities vector $q$, the actual distribution over classes is $q$. For multi-class prediction problems, however, achieving distribution calibration tends to be infeasible, requiring sample complexity exponential in the number of classes $C$. In this work, we introduce a new notion -- \emph{decision calibration} -- that requires the predicted distribution and true distribution to be ``indistinguishable'' to a set of downstream decision-makers. When all possible decision makers are under consideration, decision calibration is the same as distribution calibration. However, when we only consider decision makers choosing between a bounded number of actions (e.g. polynomial in $C$), our main result shows that decisions calibration becomes feasible -- we design a recalibration algorithm that requires sample complexity polynomial in the number of actions and the number of classes. We validate our recalibration algorithm empirically: compared to existing methods, decision calibration improves decision-making on skin lesion and ImageNet classification with modern neural network predictors.

Outcome Indistinguishability

Prediction algorithms assign numbers to individuals that are popularly understood as individual "probabilities" -- what is the probability of 5-year survival after cancer diagnosis? -- and which increasingly form the basis for life-altering decisions. Drawing on an understanding of computational indistinguishability developed in complexity theory and cryptography, we introduce Outcome Indistinguishability. Predictors that are Outcome Indistinguishable yield a generative model for outcomes that cannot be efficiently refuted on the basis of the real-life observations produced by Nature. We investigate a hierarchy of Outcome Indistinguishability definitions, whose stringency increases with the degree to which distinguishers may access the predictor in question. Our findings reveal that Outcome Indistinguishability behaves qualitatively differently than previously studied notions of indistinguishability. First, we provide constructions at all levels of the hierarchy. Then, leveraging recently-developed machinery for proving average-case fine-grained hardness, we obtain lower bounds on the complexity of the more stringent forms of Outcome Indistinguishability. This hardness result provides the first scientific grounds for the political argument that, when inspecting algorithmic risk prediction instruments, auditors should be granted oracle access to the algorithm, not simply historical predictions.

A Distributional Framework for Data Valuation

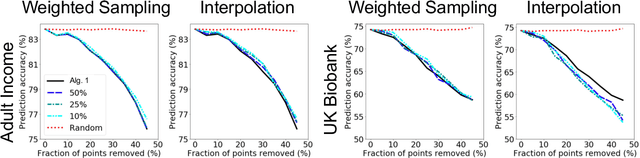
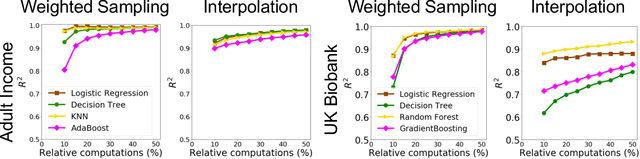
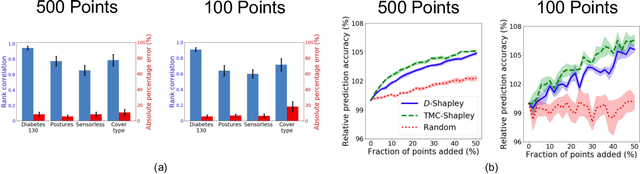
Shapley value is a classic notion from game theory, historically used to quantify the contributions of individuals within groups, and more recently applied to assign values to data points when training machine learning models. Despite its foundational role, a key limitation of the data Shapley framework is that it only provides valuations for points within a fixed data set. It does not account for statistical aspects of the data and does not give a way to reason about points outside the data set. To address these limitations, we propose a novel framework -- distributional Shapley -- where the value of a point is defined in the context of an underlying data distribution. We prove that distributional Shapley has several desirable statistical properties; for example, the values are stable under perturbations to the data points themselves and to the underlying data distribution. We leverage these properties to develop a new algorithm for estimating values from data, which comes with formal guarantees and runs two orders of magnitude faster than state-of-the-art algorithms for computing the (non-distributional) data Shapley values. We apply distributional Shapley to diverse data sets and demonstrate its utility in a data market setting.