Calibrating Predictions to Decisions: A Novel Approach to Multi-Class Calibration
Paper and Code
Jul 12, 2021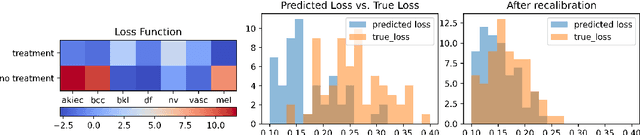


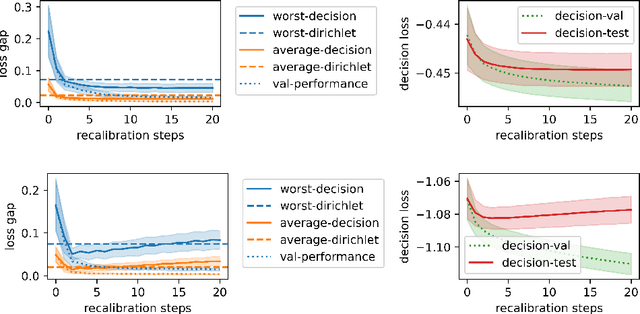
When facing uncertainty, decision-makers want predictions they can trust. A machine learning provider can convey confidence to decision-makers by guaranteeing their predictions are distribution calibrated -- amongst the inputs that receive a predicted class probabilities vector $q$, the actual distribution over classes is $q$. For multi-class prediction problems, however, achieving distribution calibration tends to be infeasible, requiring sample complexity exponential in the number of classes $C$. In this work, we introduce a new notion -- \emph{decision calibration} -- that requires the predicted distribution and true distribution to be ``indistinguishable'' to a set of downstream decision-makers. When all possible decision makers are under consideration, decision calibration is the same as distribution calibration. However, when we only consider decision makers choosing between a bounded number of actions (e.g. polynomial in $C$), our main result shows that decisions calibration becomes feasible -- we design a recalibration algorithm that requires sample complexity polynomial in the number of actions and the number of classes. We validate our recalibration algorithm empirically: compared to existing methods, decision calibration improves decision-making on skin lesion and ImageNet classification with modern neural network predictors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge