Learning from a Biased Sample

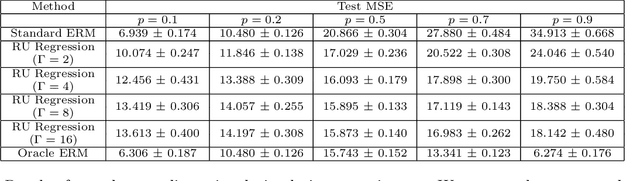
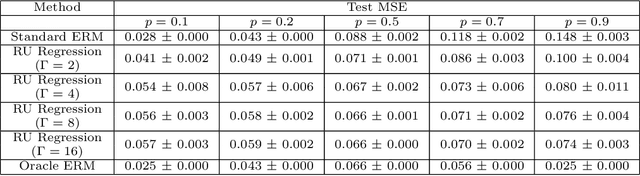
The empirical risk minimization approach to data-driven decision making assumes that we can learn a decision rule from training data drawn under the same conditions as the ones we want to deploy it under. However, in a number of settings, we may be concerned that our training sample is biased, and that some groups (characterized by either observable or unobservable attributes) may be under- or over-represented relative to the general population; and in this setting empirical risk minimization over the training set may fail to yield rules that perform well at deployment. Building on concepts from distributionally robust optimization and sensitivity analysis, we propose a method for learning a decision rule that minimizes the worst-case risk incurred under a family of test distributions whose conditional distributions of outcomes $Y$ given covariates $X$ differ from the conditional training distribution by at most a constant factor, and whose covariate distributions are absolutely continuous with respect to the covariate distribution of the training data. We apply a result of Rockafellar and Uryasev to show that this problem is equivalent to an augmented convex risk minimization problem. We give statistical guarantees for learning a robust model using the method of sieves and propose a deep learning algorithm whose loss function captures our robustness target. We empirically validate our proposed method in simulations and a case study with the MIMIC-III dataset.

Policy Learning with Competing Agents

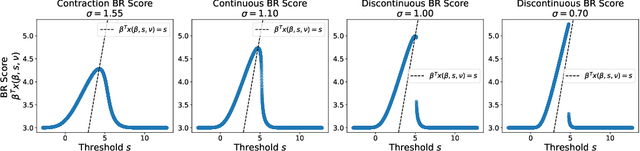
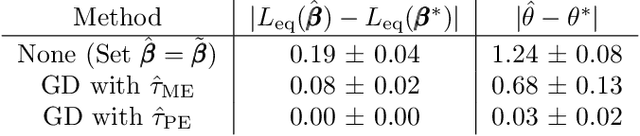
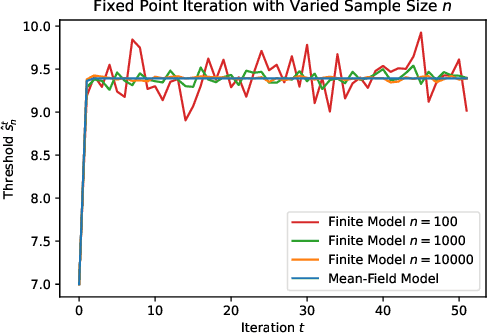
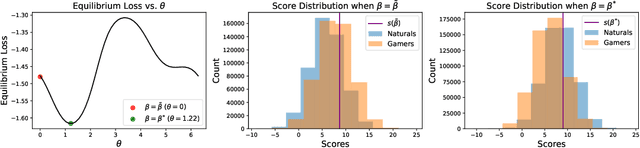
Decision makers often aim to learn a treatment assignment policy under a capacity constraint on the number of agents that they can treat. When agents can respond strategically to such policies, competition arises, complicating the estimation of the effect of the policy. In this paper, we study capacity-constrained treatment assignment in the presence of such interference. We consider a dynamic model where heterogeneous agents myopically best respond to the previous treatment assignment policy. When the number of agents is large but finite, we show that the threshold for receiving treatment under a given policy converges to the policy's mean-field equilibrium threshold. Based on this result, we develop a consistent estimator for the policy effect and demonstrate in simulations that it can be used for learning optimal capacity-constrained policies in the presence of strategic behavior.

Calibrating Predictions to Decisions: A Novel Approach to Multi-Class Calibration

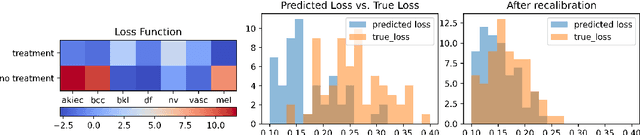
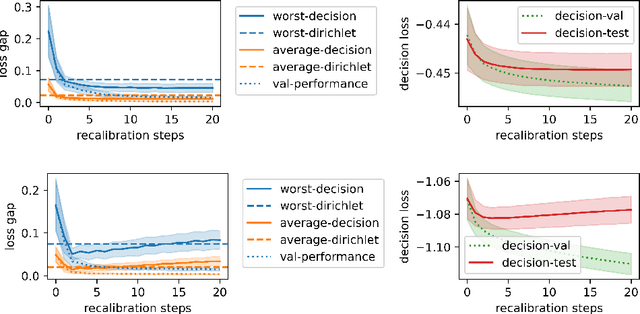
When facing uncertainty, decision-makers want predictions they can trust. A machine learning provider can convey confidence to decision-makers by guaranteeing their predictions are distribution calibrated -- amongst the inputs that receive a predicted class probabilities vector $q$, the actual distribution over classes is $q$. For multi-class prediction problems, however, achieving distribution calibration tends to be infeasible, requiring sample complexity exponential in the number of classes $C$. In this work, we introduce a new notion -- \emph{decision calibration} -- that requires the predicted distribution and true distribution to be ``indistinguishable'' to a set of downstream decision-makers. When all possible decision makers are under consideration, decision calibration is the same as distribution calibration. However, when we only consider decision makers choosing between a bounded number of actions (e.g. polynomial in $C$), our main result shows that decisions calibration becomes feasible -- we design a recalibration algorithm that requires sample complexity polynomial in the number of actions and the number of classes. We validate our recalibration algorithm empirically: compared to existing methods, decision calibration improves decision-making on skin lesion and ImageNet classification with modern neural network predictors.

Unsupervised Domain Adaptation in the Absence of Source Data

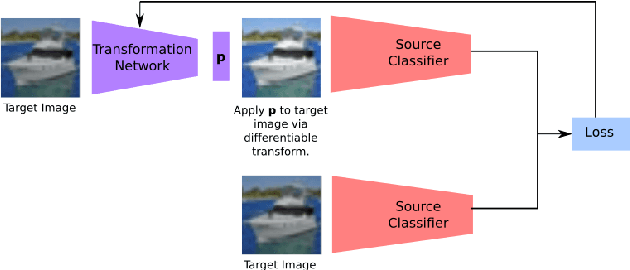
Current unsupervised domain adaptation methods can address many types of distribution shift, but they assume data from the source domain is freely available. As the use of pre-trained models becomes more prevalent, it is reasonable to assume that source data is unavailable. We propose an unsupervised method for adapting a source classifier to a target domain that varies from the source domain along natural axes, such as brightness and contrast. Our method only requires access to unlabeled target instances and the source classifier. We validate our method in scenarios where the distribution shift involves brightness, contrast, and rotation and show that it outperforms fine-tuning baselines in scenarios with limited labeled data.