Policy Learning with Competing Agents

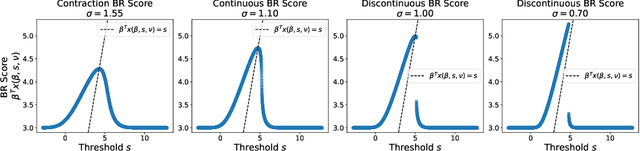
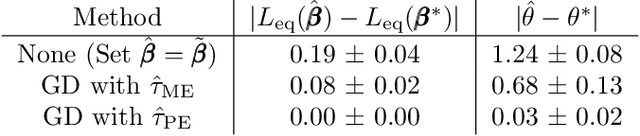
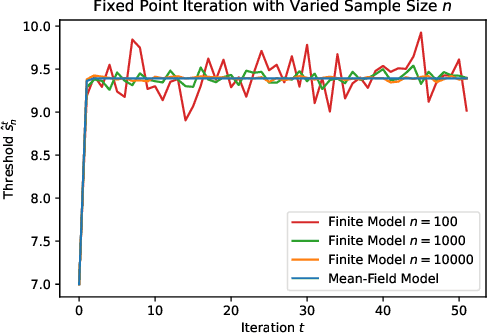
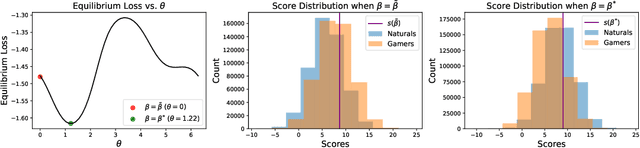
Decision makers often aim to learn a treatment assignment policy under a capacity constraint on the number of agents that they can treat. When agents can respond strategically to such policies, competition arises, complicating the estimation of the effect of the policy. In this paper, we study capacity-constrained treatment assignment in the presence of such interference. We consider a dynamic model where heterogeneous agents myopically best respond to the previous treatment assignment policy. When the number of agents is large but finite, we show that the threshold for receiving treatment under a given policy converges to the policy's mean-field equilibrium threshold. Based on this result, we develop a consistent estimator for the policy effect and demonstrate in simulations that it can be used for learning optimal capacity-constrained policies in the presence of strategic behavior.