A Cryptographic Perspective on Mitigation vs. Detection in Machine Learning

In this paper, we initiate a cryptographically inspired theoretical study of detection versus mitigation of adversarial inputs produced by attackers of Machine Learning algorithms during inference time. We formally define defense by detection (DbD) and defense by mitigation (DbM). Our definitions come in the form of a 3-round protocol between two resource-bounded parties: a trainer/defender and an attacker. The attacker aims to produce inference-time inputs that fool the training algorithm. We define correctness, completeness, and soundness properties to capture successful defense at inference time while not degrading (too much) the performance of the algorithm on inputs from the training distribution. We first show that achieving DbD and achieving DbM are equivalent for ML classification tasks. Surprisingly, this is not the case for ML generative learning tasks, where there are many possible correct outputs that can be generated for each input. We show a separation between DbD and DbM by exhibiting a generative learning task for which is possible to defend by mitigation but is provably impossible to defend by detection under the assumption that the Identity-Based Fully Homomorphic Encryption (IB-FHE), publicly-verifiable zero-knowledge Succinct Non-Interactive Arguments of Knowledge (zk-SNARK) and Strongly Unforgeable Signatures exist. The mitigation phase uses significantly fewer samples than the initial training algorithm.

Unsupervised Translation of Emergent Communication

Emergent Communication (EC) provides a unique window into the language systems that emerge autonomously when agents are trained to jointly achieve shared goals. However, it is difficult to interpret EC and evaluate its relationship with natural languages (NL). This study employs unsupervised neural machine translation (UNMT) techniques to decipher ECs formed during referential games with varying task complexities, influenced by the semantic diversity of the environment. Our findings demonstrate UNMT's potential to translate EC, illustrating that task complexity characterized by semantic diversity enhances EC translatability, while higher task complexity with constrained semantic variability exhibits pragmatic EC, which, although challenging to interpret, remains suitable for translation. This research marks the first attempt, to our knowledge, to translate EC without the aid of parallel data.

Learning Randomized Reductions and Program Properties

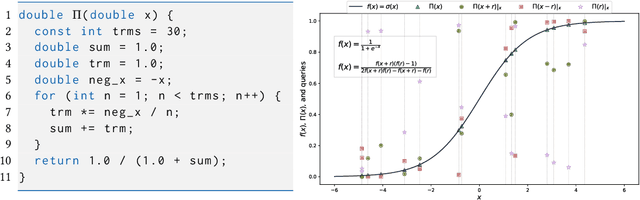
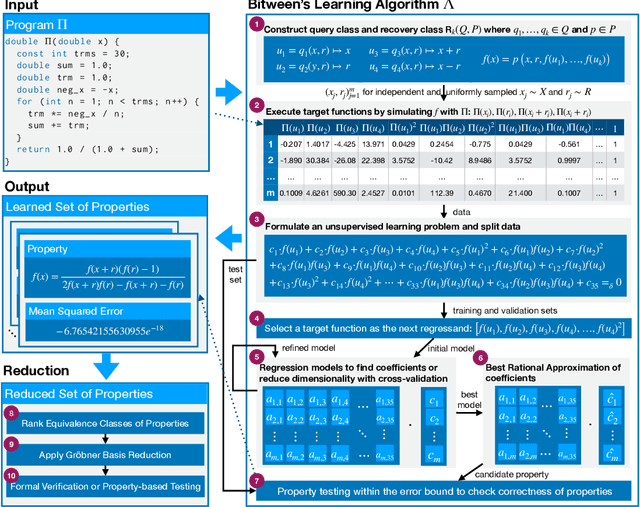
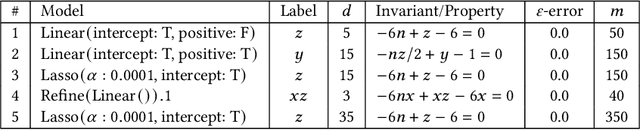
The correctness of computations remains a significant challenge in computer science, with traditional approaches relying on automated testing or formal verification. Self-testing/correcting programs introduce an alternative paradigm, allowing a program to verify and correct its own outputs via randomized reductions, a concept that previously required manual derivation. In this paper, we present Bitween, a method and tool for automated learning of randomized (self)-reductions and program properties in numerical programs. Bitween combines symbolic analysis and machine learning, with a surprising finding: polynomial-time linear regression, a basic optimization method, is not only sufficient but also highly effective for deriving complex randomized self-reductions and program invariants, often outperforming sophisticated mixed-integer linear programming solvers. We establish a theoretical framework for learning these reductions and introduce RSR-Bench, a benchmark suite for evaluating Bitween's capabilities on scientific and machine learning functions. Our empirical results show that Bitween surpasses state-of-the-art tools in scalability, stability, and sample efficiency when evaluated on nonlinear invariant benchmarks like NLA-DigBench. Bitween is open-source as a Python package and accessible via a web interface that supports C language programs.

Oblivious Defense in ML Models: Backdoor Removal without Detection

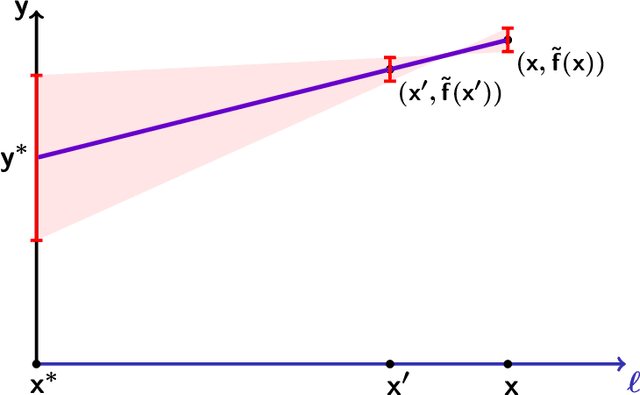
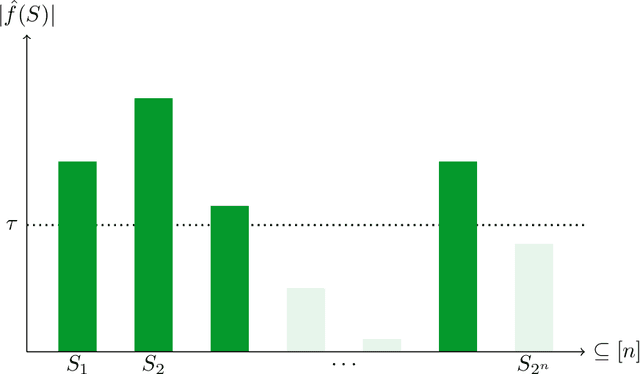
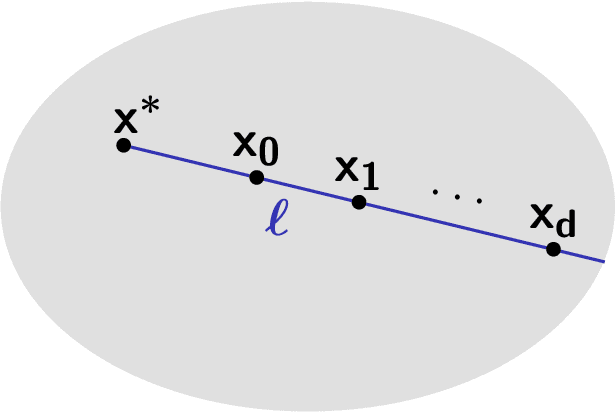
As society grows more reliant on machine learning, ensuring the security of machine learning systems against sophisticated attacks becomes a pressing concern. A recent result of Goldwasser, Kim, Vaikuntanathan, and Zamir (2022) shows that an adversary can plant undetectable backdoors in machine learning models, allowing the adversary to covertly control the model's behavior. Backdoors can be planted in such a way that the backdoored machine learning model is computationally indistinguishable from an honest model without backdoors. In this paper, we present strategies for defending against backdoors in ML models, even if they are undetectable. The key observation is that it is sometimes possible to provably mitigate or even remove backdoors without needing to detect them, using techniques inspired by the notion of random self-reducibility. This depends on properties of the ground-truth labels (chosen by nature), and not of the proposed ML model (which may be chosen by an attacker). We give formal definitions for secure backdoor mitigation, and proceed to show two types of results. First, we show a "global mitigation" technique, which removes all backdoors from a machine learning model under the assumption that the ground-truth labels are close to a Fourier-heavy function. Second, we consider distributions where the ground-truth labels are close to a linear or polynomial function in $\mathbb{R}^n$. Here, we show "local mitigation" techniques, which remove backdoors with high probability for every inputs of interest, and are computationally cheaper than global mitigation. All of our constructions are black-box, so our techniques work without needing access to the model's representation (i.e., its code or parameters). Along the way we prove a simple result for robust mean estimation.

Models That Prove Their Own Correctness

How can we trust the correctness of a learned model on a particular input of interest? Model accuracy is typically measured \emph{on average} over a distribution of inputs, giving no guarantee for any fixed input. This paper proposes a theoretically-founded solution to this problem: to train *Self-Proving models* that prove the correctness of their output to a verification algorithm $V$ via an Interactive Proof. Self-Proving models satisfy that, with high probability over a random input, the model generates a correct output \emph{and} successfully proves its correctness to $V\!$. The *soundness* property of $V$ guarantees that, for *every* input, no model can convince $V$ of the correctness of an incorrect output. Thus, a Self-Proving model proves correctness of most of its outputs, while *all* incorrect outputs (of any model) are detected by $V$. We devise a generic method for learning Self-Proving models, and we prove convergence bounds under certain assumptions. The theoretical framework and results are complemented by experiments on an arithmetic capability: computing the greatest common divisor (GCD) of two integers. Our learning method is used to train a Self-Proving transformer that computes the GCD *and* proves the correctness of its answer.

A Theory of Unsupervised Translation Motivated by Understanding Animal Communication

Recent years have seen breakthroughs in neural language models that capture nuances of language, culture, and knowledge. Neural networks are capable of translating between languages -- in some cases even between two languages where there is little or no access to parallel translations, in what is known as Unsupervised Machine Translation (UMT). Given this progress, it is intriguing to ask whether machine learning tools can ultimately enable understanding animal communication, particularly that of highly intelligent animals. Our work is motivated by an ambitious interdisciplinary initiative, Project CETI, which is collecting a large corpus of sperm whale communications for machine analysis. We propose a theoretical framework for analyzing UMT when no parallel data are available and when it cannot be assumed that the source and target corpora address related subject domains or posses similar linguistic structure. The framework requires access to a prior probability distribution that should assign non-zero probability to possible translations. We instantiate our framework with two models of language. Our analysis suggests that accuracy of translation depends on the complexity of the source language and the amount of ``common ground'' between the source language and target prior. We also prove upper bounds on the amount of data required from the source language in the unsupervised setting as a function of the amount of data required in a hypothetical supervised setting. Surprisingly, our bounds suggest that the amount of source data required for unsupervised translation is comparable to the supervised setting. For one of the language models which we analyze we also prove a nearly matching lower bound. Our analysis is purely information-theoretic and as such can inform how much source data needs to be collected, but does not yield a computationally efficient procedure.

Planting Undetectable Backdoors in Machine Learning Models

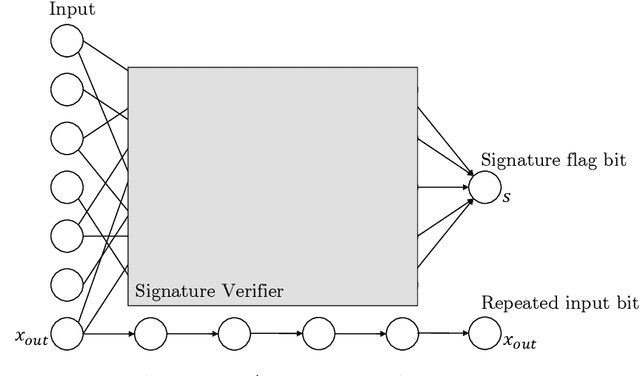
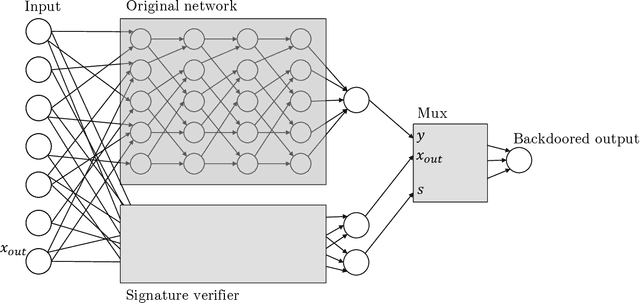
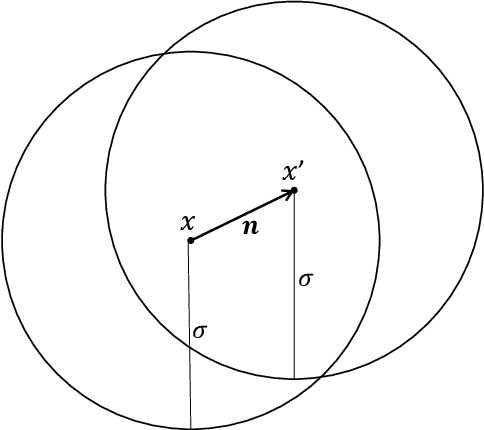
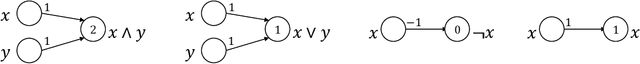
Given the computational cost and technical expertise required to train machine learning models, users may delegate the task of learning to a service provider. We show how a malicious learner can plant an undetectable backdoor into a classifier. On the surface, such a backdoored classifier behaves normally, but in reality, the learner maintains a mechanism for changing the classification of any input, with only a slight perturbation. Importantly, without the appropriate "backdoor key", the mechanism is hidden and cannot be detected by any computationally-bounded observer. We demonstrate two frameworks for planting undetectable backdoors, with incomparable guarantees. First, we show how to plant a backdoor in any model, using digital signature schemes. The construction guarantees that given black-box access to the original model and the backdoored version, it is computationally infeasible to find even a single input where they differ. This property implies that the backdoored model has generalization error comparable with the original model. Second, we demonstrate how to insert undetectable backdoors in models trained using the Random Fourier Features (RFF) learning paradigm or in Random ReLU networks. In this construction, undetectability holds against powerful white-box distinguishers: given a complete description of the network and the training data, no efficient distinguisher can guess whether the model is "clean" or contains a backdoor. Our construction of undetectable backdoors also sheds light on the related issue of robustness to adversarial examples. In particular, our construction can produce a classifier that is indistinguishable from an "adversarially robust" classifier, but where every input has an adversarial example! In summary, the existence of undetectable backdoors represent a significant theoretical roadblock to certifying adversarial robustness.

Cetacean Translation Initiative: a roadmap to deciphering the communication of sperm whales

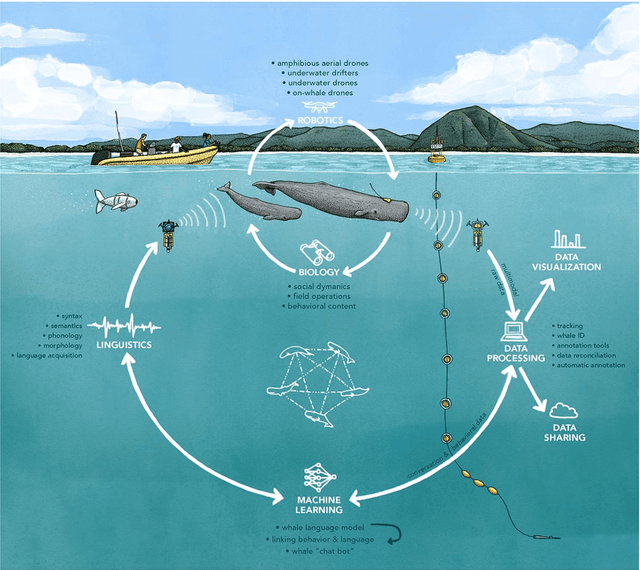
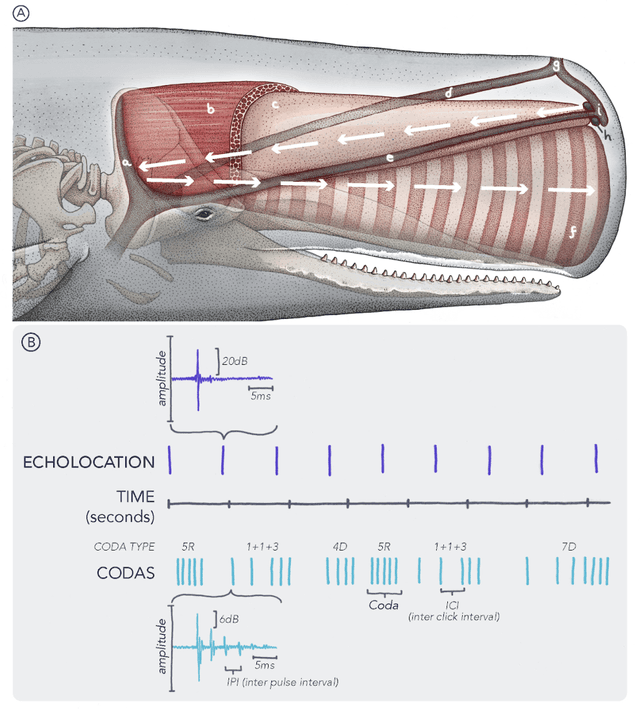
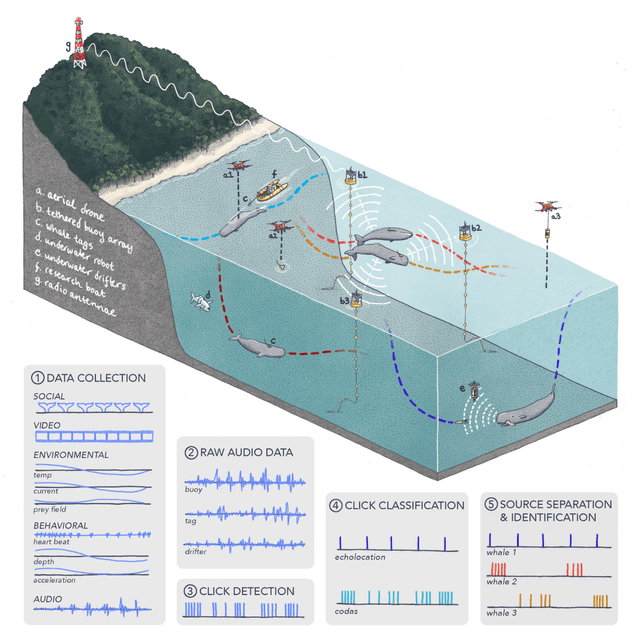
The past decade has witnessed a groundbreaking rise of machine learning for human language analysis, with current methods capable of automatically accurately recovering various aspects of syntax and semantics - including sentence structure and grounded word meaning - from large data collections. Recent research showed the promise of such tools for analyzing acoustic communication in nonhuman species. We posit that machine learning will be the cornerstone of future collection, processing, and analysis of multimodal streams of data in animal communication studies, including bioacoustic, behavioral, biological, and environmental data. Cetaceans are unique non-human model species as they possess sophisticated acoustic communications, but utilize a very different encoding system that evolved in an aquatic rather than terrestrial medium. Sperm whales, in particular, with their highly-developed neuroanatomical features, cognitive abilities, social structures, and discrete click-based encoding make for an excellent starting point for advanced machine learning tools that can be applied to other animals in the future. This paper details a roadmap toward this goal based on currently existing technology and multidisciplinary scientific community effort. We outline the key elements required for the collection and processing of massive bioacoustic data of sperm whales, detecting their basic communication units and language-like higher-level structures, and validating these models through interactive playback experiments. The technological capabilities developed by such an undertaking are likely to yield cross-applications and advancements in broader communities investigating non-human communication and animal behavioral research.

Beyond Perturbations: Learning Guarantees with Arbitrary Adversarial Test Examples

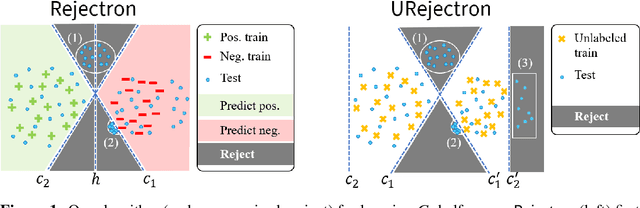
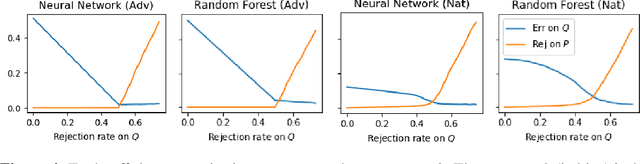
We present a transductive learning algorithm that takes as input training examples from a distribution $P$ and arbitrary (unlabeled) test examples, possibly chosen by an adversary. This is unlike prior work that assumes that test examples are small perturbations of $P$. Our algorithm outputs a selective classifier, which abstains from predicting on some examples. By considering selective transductive learning, we give the first nontrivial guarantees for learning classes of bounded VC dimension with arbitrary train and test distributions---no prior guarantees were known even for simple classes of functions such as intervals on the line. In particular, for any function in a class $C$ of bounded VC dimension, we guarantee a low test error rate and a low rejection rate with respect to $P$. Our algorithm is efficient given an Empirical Risk Minimizer (ERM) for $C$. Our guarantees hold even for test examples chosen by an unbounded white-box adversary. We also give guarantees for generalization, agnostic, and unsupervised settings.