Oblivious Defense in ML Models: Backdoor Removal without Detection

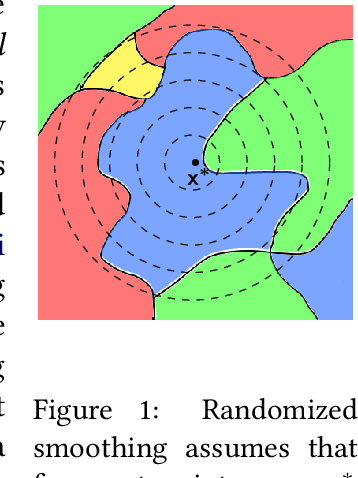
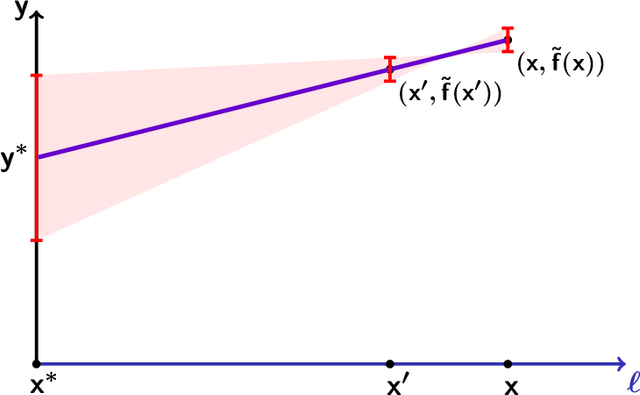
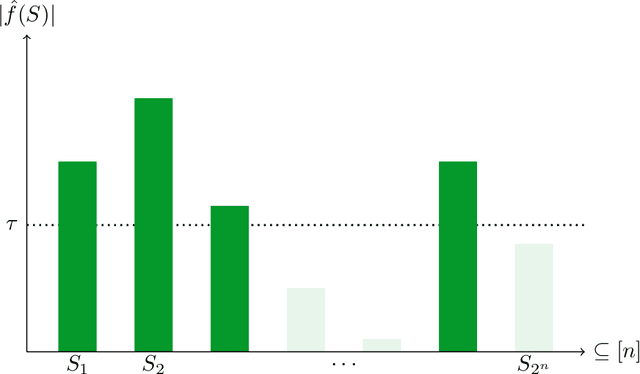
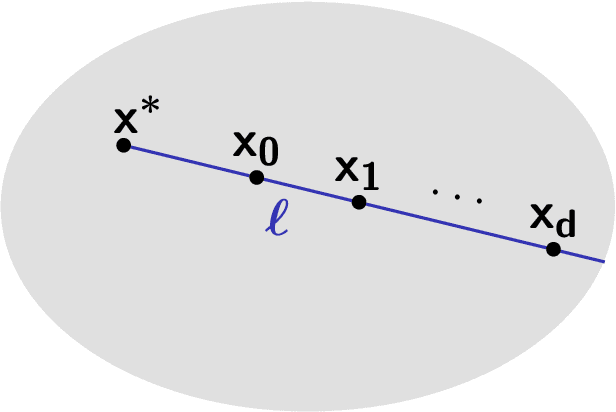
As society grows more reliant on machine learning, ensuring the security of machine learning systems against sophisticated attacks becomes a pressing concern. A recent result of Goldwasser, Kim, Vaikuntanathan, and Zamir (2022) shows that an adversary can plant undetectable backdoors in machine learning models, allowing the adversary to covertly control the model's behavior. Backdoors can be planted in such a way that the backdoored machine learning model is computationally indistinguishable from an honest model without backdoors. In this paper, we present strategies for defending against backdoors in ML models, even if they are undetectable. The key observation is that it is sometimes possible to provably mitigate or even remove backdoors without needing to detect them, using techniques inspired by the notion of random self-reducibility. This depends on properties of the ground-truth labels (chosen by nature), and not of the proposed ML model (which may be chosen by an attacker). We give formal definitions for secure backdoor mitigation, and proceed to show two types of results. First, we show a "global mitigation" technique, which removes all backdoors from a machine learning model under the assumption that the ground-truth labels are close to a Fourier-heavy function. Second, we consider distributions where the ground-truth labels are close to a linear or polynomial function in $\mathbb{R}^n$. Here, we show "local mitigation" techniques, which remove backdoors with high probability for every inputs of interest, and are computationally cheaper than global mitigation. All of our constructions are black-box, so our techniques work without needing access to the model's representation (i.e., its code or parameters). Along the way we prove a simple result for robust mean estimation.

Sparse Linear Regression and Lattice Problems

Sparse linear regression (SLR) is a well-studied problem in statistics where one is given a design matrix $X\in\mathbb{R}^{m\times n}$ and a response vector $y=X\theta^*+w$ for a $k$-sparse vector $\theta^*$ (that is, $\|\theta^*\|_0\leq k$) and small, arbitrary noise $w$, and the goal is to find a $k$-sparse $\widehat{\theta} \in \mathbb{R}^n$ that minimizes the mean squared prediction error $\frac{1}{m}\|X\widehat{\theta}-X\theta^*\|^2_2$. While $\ell_1$-relaxation methods such as basis pursuit, Lasso, and the Dantzig selector solve SLR when the design matrix is well-conditioned, no general algorithm is known, nor is there any formal evidence of hardness in an average-case setting with respect to all efficient algorithms. We give evidence of average-case hardness of SLR w.r.t. all efficient algorithms assuming the worst-case hardness of lattice problems. Specifically, we give an instance-by-instance reduction from a variant of the bounded distance decoding (BDD) problem on lattices to SLR, where the condition number of the lattice basis that defines the BDD instance is directly related to the restricted eigenvalue condition of the design matrix, which characterizes some of the classical statistical-computational gaps for sparse linear regression. Also, by appealing to worst-case to average-case reductions from the world of lattices, this shows hardness for a distribution of SLR instances; while the design matrices are ill-conditioned, the resulting SLR instances are in the identifiable regime. Furthermore, for well-conditioned (essentially) isotropic Gaussian design matrices, where Lasso is known to behave well in the identifiable regime, we show hardness of outputting any good solution in the unidentifiable regime where there are many solutions, assuming the worst-case hardness of standard and well-studied lattice problems.

Continuous LWE is as Hard as LWE & Applications to Learning Gaussian Mixtures

We show direct and conceptually simple reductions between the classical learning with errors (LWE) problem and its continuous analog, CLWE (Bruna, Regev, Song and Tang, STOC 2021). This allows us to bring to bear the powerful machinery of LWE-based cryptography to the applications of CLWE. For example, we obtain the hardness of CLWE under the classical worst-case hardness of the gap shortest vector problem. Previously, this was known only under quantum worst-case hardness of lattice problems. More broadly, with our reductions between the two problems, any future developments to LWE will also apply to CLWE and its downstream applications. As a concrete application, we show an improved hardness result for density estimation for mixtures of Gaussians. In this computational problem, given sample access to a mixture of Gaussians, the goal is to output a function that estimates the density function of the mixture. Under the (plausible and widely believed) exponential hardness of the classical LWE problem, we show that Gaussian mixture density estimation in $\mathbb{R}^n$ with roughly $\log n$ Gaussian components given $\mathsf{poly}(n)$ samples requires time quasi-polynomial in $n$. Under the (conservative) polynomial hardness of LWE, we show hardness of density estimation for $n^{\epsilon}$ Gaussians for any constant $\epsilon > 0$, which improves on Bruna, Regev, Song and Tang (STOC 2021), who show hardness for at least $\sqrt{n}$ Gaussians under polynomial (quantum) hardness assumptions. Our key technical tool is a reduction from classical LWE to LWE with $k$-sparse secrets where the multiplicative increase in the noise is only $O(\sqrt{k})$, independent of the ambient dimension $n$.