Learning Randomized Reductions and Program Properties

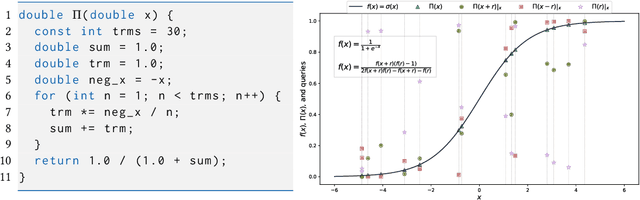
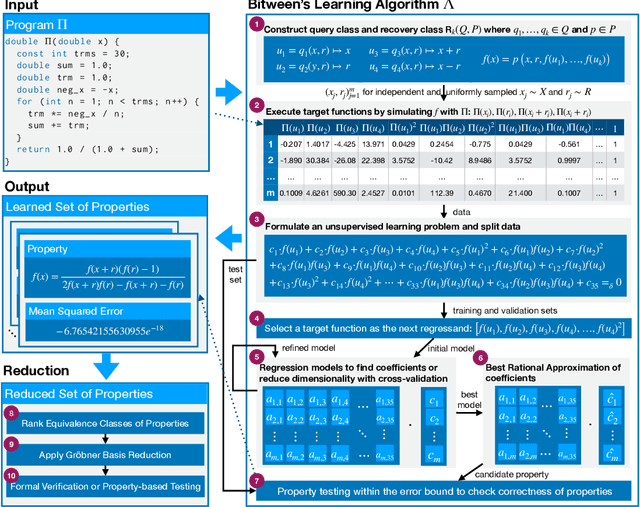
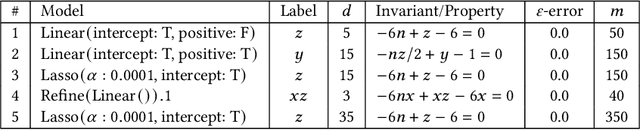
The correctness of computations remains a significant challenge in computer science, with traditional approaches relying on automated testing or formal verification. Self-testing/correcting programs introduce an alternative paradigm, allowing a program to verify and correct its own outputs via randomized reductions, a concept that previously required manual derivation. In this paper, we present Bitween, a method and tool for automated learning of randomized (self)-reductions and program properties in numerical programs. Bitween combines symbolic analysis and machine learning, with a surprising finding: polynomial-time linear regression, a basic optimization method, is not only sufficient but also highly effective for deriving complex randomized self-reductions and program invariants, often outperforming sophisticated mixed-integer linear programming solvers. We establish a theoretical framework for learning these reductions and introduce RSR-Bench, a benchmark suite for evaluating Bitween's capabilities on scientific and machine learning functions. Our empirical results show that Bitween surpasses state-of-the-art tools in scalability, stability, and sample efficiency when evaluated on nonlinear invariant benchmarks like NLA-DigBench. Bitween is open-source as a Python package and accessible via a web interface that supports C language programs.

Harnessing Neuron Stability to Improve DNN Verification

Deep Neural Networks (DNN) have emerged as an effective approach to tackling real-world problems. However, like human-written software, DNNs are susceptible to bugs and attacks. This has generated significant interests in developing effective and scalable DNN verification techniques and tools. In this paper, we present VeriStable, a novel extension of recently proposed DPLL-based constraint DNN verification approach. VeriStable leverages the insight that while neuron behavior may be non-linear across the entire DNN input space, at intermediate states computed during verification many neurons may be constrained to have linear behavior - these neurons are stable. Efficiently detecting stable neurons reduces combinatorial complexity without compromising the precision of abstractions. Moreover, the structure of clauses arising in DNN verification problems shares important characteristics with industrial SAT benchmarks. We adapt and incorporate multi-threading and restart optimizations targeting those characteristics to further optimize DPLL-based DNN verification. We evaluate the effectiveness of VeriStable across a range of challenging benchmarks including fully-connected feedforward networks (FNNs), convolutional neural networks (CNNs) and residual networks (ResNets) applied to the standard MNIST and CIFAR datasets. Preliminary results show that VeriStable is competitive and outperforms state-of-the-art DNN verification tools, including $\alpha$-$\beta$-CROWN and MN-BaB, the first and second performers of the VNN-COMP, respectively.

A DPLL Framework for Verifying Deep Neural Networks

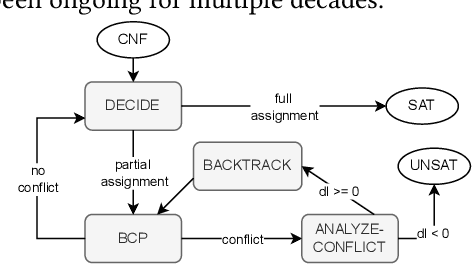
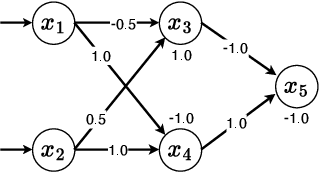
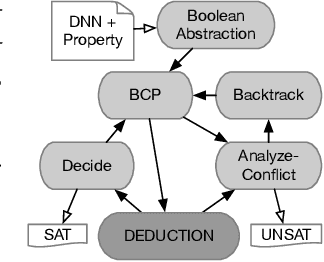
Deep Neural Networks (DNNs) have emerged as an effective approach to tackling real-world problems. However, like human-written software, automatically-generated DNNs can have bugs and be attacked. This thus attracts many recent interests in developing effective and scalable DNN verification techniques and tools. In this work, we introduce a NeuralSAT, a new constraint solving approach to DNN verification. The design of NeuralSAT follows the DPLL(T) algorithm used modern SMT solving, which includes (conflict) clause learning, abstraction, and theory solving, and thus NeuralSAT can be considered as an SMT framework for DNNs. Preliminary results show that the NeuralSAT prototype is competitive to the state-of-the-art. We hope, with proper optimization and engineering, NeuralSAT will carry the power and success of modern SAT/SMT solvers to DNN verification. NeuralSAT is avaliable from: https://github.com/dynaroars/neuralsat-solver