Excuse me, sir? Your language model is leaking

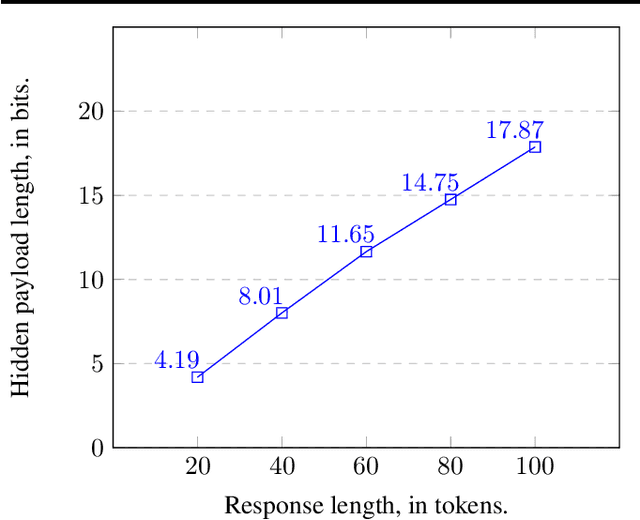
We introduce a cryptographic method to hide an arbitrary secret payload in the response of a Large Language Model (LLM). A secret key is required to extract the payload from the model's response, and without the key it is provably impossible to distinguish between the responses of the original LLM and the LLM that hides a payload. In particular, the quality of generated text is not affected by the payload. Our approach extends a recent result of Christ, Gunn and Zamir (2023) who introduced an undetectable watermarking scheme for LLMs.

Planting Undetectable Backdoors in Machine Learning Models

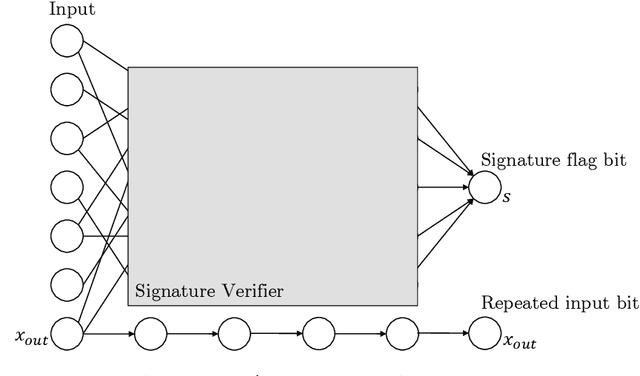
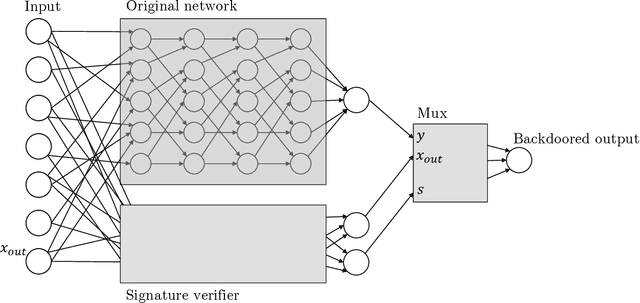
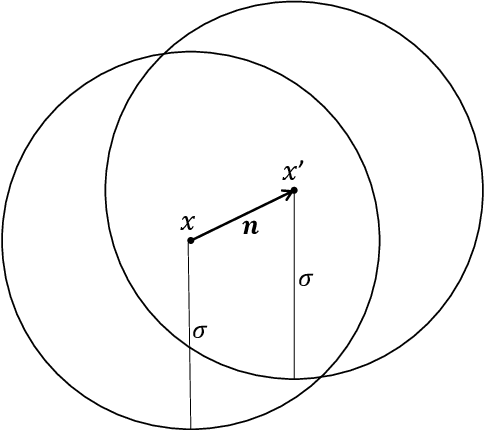
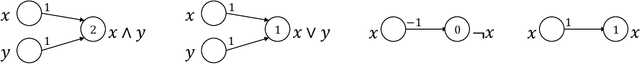
Given the computational cost and technical expertise required to train machine learning models, users may delegate the task of learning to a service provider. We show how a malicious learner can plant an undetectable backdoor into a classifier. On the surface, such a backdoored classifier behaves normally, but in reality, the learner maintains a mechanism for changing the classification of any input, with only a slight perturbation. Importantly, without the appropriate "backdoor key", the mechanism is hidden and cannot be detected by any computationally-bounded observer. We demonstrate two frameworks for planting undetectable backdoors, with incomparable guarantees. First, we show how to plant a backdoor in any model, using digital signature schemes. The construction guarantees that given black-box access to the original model and the backdoored version, it is computationally infeasible to find even a single input where they differ. This property implies that the backdoored model has generalization error comparable with the original model. Second, we demonstrate how to insert undetectable backdoors in models trained using the Random Fourier Features (RFF) learning paradigm or in Random ReLU networks. In this construction, undetectability holds against powerful white-box distinguishers: given a complete description of the network and the training data, no efficient distinguisher can guess whether the model is "clean" or contains a backdoor. Our construction of undetectable backdoors also sheds light on the related issue of robustness to adversarial examples. In particular, our construction can produce a classifier that is indistinguishable from an "adversarially robust" classifier, but where every input has an adversarial example! In summary, the existence of undetectable backdoors represent a significant theoretical roadblock to certifying adversarial robustness.

Randomized Dimensionality Reduction for Facility Location and Single-Linkage Clustering

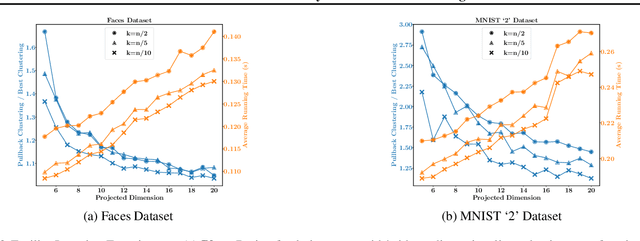
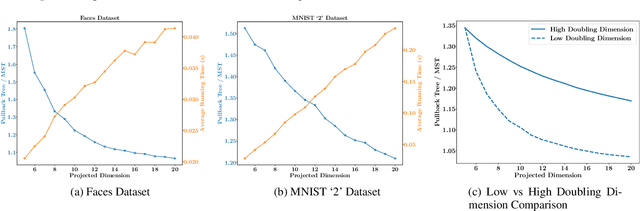
Random dimensionality reduction is a versatile tool for speeding up algorithms for high-dimensional problems. We study its application to two clustering problems: the facility location problem, and the single-linkage hierarchical clustering problem, which is equivalent to computing the minimum spanning tree. We show that if we project the input pointset $X$ onto a random $d = O(d_X)$-dimensional subspace (where $d_X$ is the doubling dimension of $X$), then the optimum facility location cost in the projected space approximates the original cost up to a constant factor. We show an analogous statement for minimum spanning tree, but with the dimension $d$ having an extra $\log \log n$ term and the approximation factor being arbitrarily close to $1$. Furthermore, we extend these results to approximating solutions instead of just their costs. Lastly, we provide experimental results to validate the quality of solutions and the speedup due to the dimensionality reduction. Unlike several previous papers studying this approach in the context of $k$-means and $k$-medians, our dimension bound does not depend on the number of clusters but only on the intrinsic dimensionality of $X$.

Motion Planning for Unlabeled Discs with Optimality Guarantees

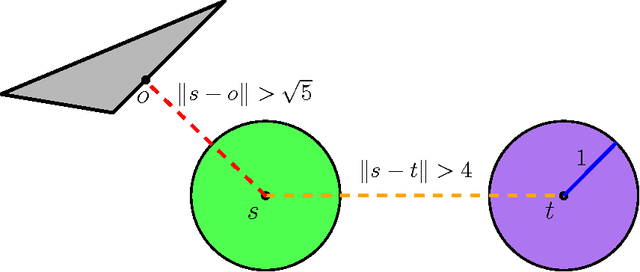
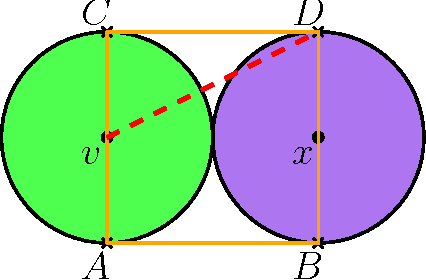
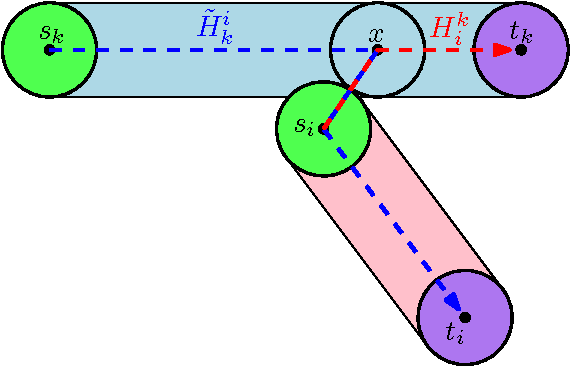
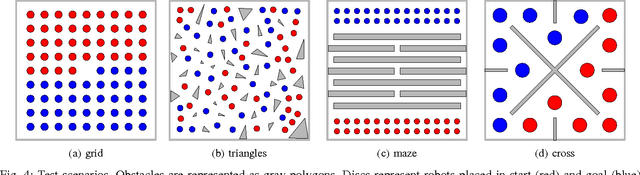
We study the problem of path planning for unlabeled (indistinguishable) unit-disc robots in a planar environment cluttered with polygonal obstacles. We introduce an algorithm which minimizes the total path length, i.e., the sum of lengths of the individual paths. Our algorithm is guaranteed to find a solution if one exists, or report that none exists otherwise. It runs in time $\tilde{O}(m^4+m^2n^2)$, where $m$ is the number of robots and $n$ is the total complexity of the workspace. Moreover, the total length of the returned solution is at most $\text{OPT}+4m$, where OPT is the optimal solution cost. To the best of our knowledge this is the first algorithm for the problem that has such guarantees. The algorithm has been implemented in an exact manner and we present experimental results that attest to its efficiency.