Randomized Dimensionality Reduction for Facility Location and Single-Linkage Clustering
Paper and Code
Jul 05, 2021
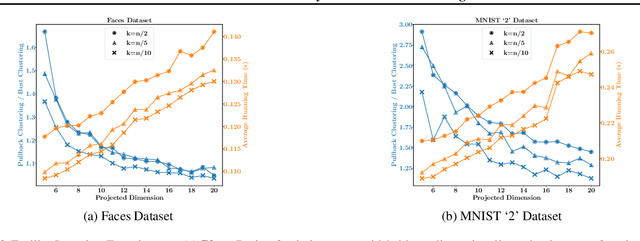
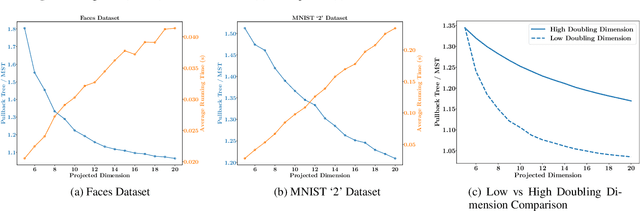
Random dimensionality reduction is a versatile tool for speeding up algorithms for high-dimensional problems. We study its application to two clustering problems: the facility location problem, and the single-linkage hierarchical clustering problem, which is equivalent to computing the minimum spanning tree. We show that if we project the input pointset $X$ onto a random $d = O(d_X)$-dimensional subspace (where $d_X$ is the doubling dimension of $X$), then the optimum facility location cost in the projected space approximates the original cost up to a constant factor. We show an analogous statement for minimum spanning tree, but with the dimension $d$ having an extra $\log \log n$ term and the approximation factor being arbitrarily close to $1$. Furthermore, we extend these results to approximating solutions instead of just their costs. Lastly, we provide experimental results to validate the quality of solutions and the speedup due to the dimensionality reduction. Unlike several previous papers studying this approach in the context of $k$-means and $k$-medians, our dimension bound does not depend on the number of clusters but only on the intrinsic dimensionality of $X$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge