Dan Halperin
Algorithms for Nonlinear Mixed-Integer Location Estimation
May 19, 2025Abstract:For three decades, carrier-phase observations have been used to obtain the most accurate location estimates using global navigation satellite systems (GNSS). These estimates are computed by minimizing a nonlinear mixed-integer least-squares problem. Existing algorithms linearize the problem, orthogonally project it to eliminate real variables, and then solve the integer least-square problem. There is now considerable interest in developing similar localization techniques for terrestrial and indoor settings. We show that algorithms that linearize first fail in these settings and we propose several algorithms for computing the estimates. Some of our algorithms are elimination algorithms that start by eliminating the non-linear terms in the constraints; others construct a geometric arrangement that allows us to efficiently enumerate integer solutions (in polynomial time). We focus on simplified localization problems in which the measurements are range (distance) measurements and carrier phase range measurements, with no nuisance parameters. The simplified problem allows us to focus on the core question of untangling the nonlinearity and the integer nature of some parameters. We show using simulations that the new algorithms are effective at close ranges at which the linearize-first approach fails.
Point Cloud Based Scene Segmentation: A Survey
Mar 16, 2025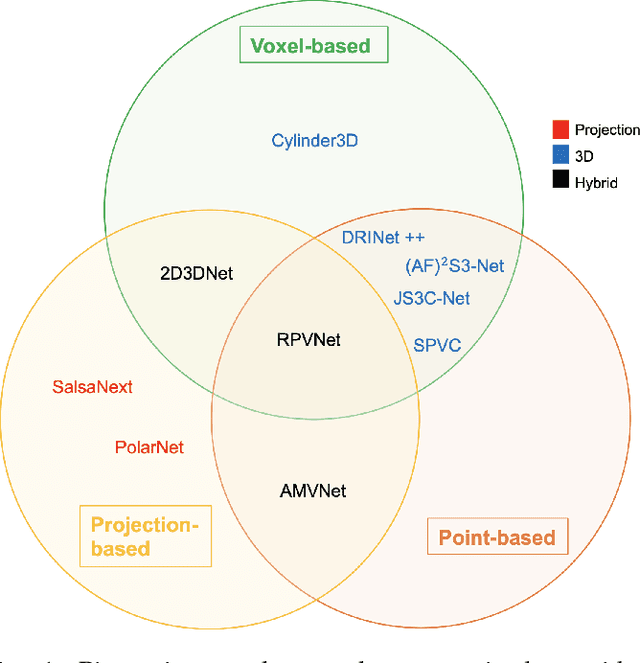
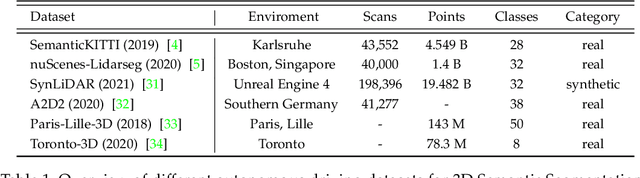

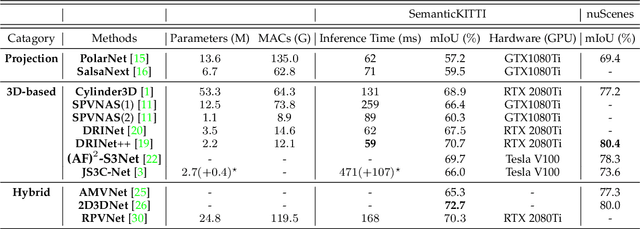
Abstract:Autonomous driving is a safety-critical application, and it is therefore a top priority that the accompanying assistance systems are able to provide precise information about the surrounding environment of the vehicle. Tasks such as 3D Object Detection deliver an insufficiently detailed understanding of the surrounding scene because they only predict a bounding box for foreground objects. In contrast, 3D Semantic Segmentation provides richer and denser information about the environment by assigning a label to each individual point, which is of paramount importance for autonomous driving tasks, such as navigation or lane changes. To inspire future research, in this review paper, we provide a comprehensive overview of the current state-of-the-art methods in the field of Point Cloud Semantic Segmentation for autonomous driving. We categorize the approaches into projection-based, 3D-based and hybrid methods. Moreover, we discuss the most important and commonly used datasets for this task and also emphasize the importance of synthetic data to support research when real-world data is limited. We further present the results of the different methods and compare them with respect to their segmentation accuracy and efficiency.
A Note on the Time Complexity of Using Subdivision Methods for the Approximation of Fibers
Mar 03, 2025Abstract:Subdivision methods such as quadtrees, octrees, and higher-dimensional orthrees are standard practice in different domains of computer science. We can use these methods to represent given geometries, such as curves, meshes, or surfaces. This representation is achieved by splitting some bounding voxel recursively while further splitting only sub-voxels that intersect with the given geometry. It is fairly known that subdivision methods are more efficient than traversing a fine-grained voxel grid. In this short note, we propose another outlook on analyzing the construction time complexity of orthrees to represent implicitly defined geometries that are fibers (preimages) of some function. This complexity is indeed asymptotically better than traversing dense voxel grids, under certain conditions, which we specify in the note. In fact, the complexity is output sensitive, and is closely related to the Hausdorff measure and Hausdorff dimension of the resulting geometry.
Ten Problems in Geobotics
Aug 26, 2024Abstract:Robots sense, move and act in the physical world. It is therefore natural that algorithmic problems in robotics and automation have a geometric component, often central to the problem. Below we review ten challenging problems at the intersection of robotics and computational geometry -- let's call this intersection Geobotics. What is common to most of these problems is that the prevalent algorithmic techniques used in robotics do not seem suitable for solving them, or at least do not suggest quality guarantees for the solution. Solving some of them, even partially, can shed light on less well-understood aspects of computation in robotics.
Localization in Dynamic Planar Environments Using Few Distance Measurements
Jul 03, 2024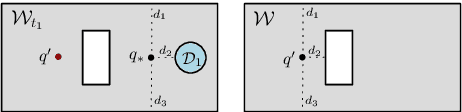
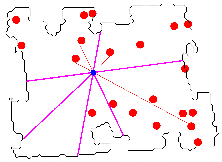
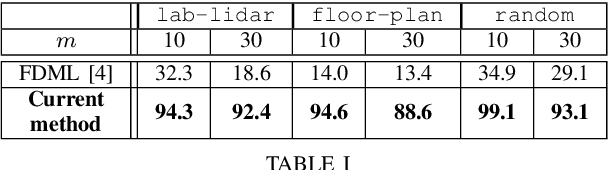
Abstract:We present a method for determining the unknown location of a sensor placed in a known 2D environment in the presence of unknown dynamic obstacles, using only few distance measurements. We present guarantees on the quality of the localization, which are robust under mild assumptions on the density of the unknown/dynamic obstacles in the known environment. We demonstrate the effectiveness of our method in simulated experiments for different environments and varying dynamic-obstacle density. Our open source software is available at https://github.com/TAU-CGL/vb-fdml2-public.
Near-Optimal Min-Sum Motion Planning for Two Square Robots in a Polygonal Environment
Oct 31, 2023Abstract:Let $\mathcal{W} \subset \mathbb{R}^2$ be a planar polygonal environment (i.e., a polygon potentially with holes) with a total of $n$ vertices, and let $A,B$ be two robots, each modeled as an axis-aligned unit square, that can translate inside $\mathcal{W}$. Given source and target placements $s_A,t_A,s_B,t_B \in \mathcal{W}$ of $A$ and $B$, respectively, the goal is to compute a \emph{collision-free motion plan} $\mathbf{\pi}^*$, i.e., a motion plan that continuously moves $A$ from $s_A$ to $t_A$ and $B$ from $s_B$ to $t_B$ so that $A$ and $B$ remain inside $\mathcal{W}$ and do not collide with each other during the motion. Furthermore, if such a plan exists, then we wish to return a plan that minimizes the sum of the lengths of the paths traversed by the robots, $\left|\mathbf{\pi}^*\right|$. Given $\mathcal{W}, s_A,t_A,s_B,t_B$ and a parameter $\varepsilon > 0$, we present an $n^2\varepsilon^{-O(1)} \log n$-time $(1+\varepsilon)$-approximation algorithm for this problem. We are not aware of any polynomial time algorithm for this problem, nor do we know whether the problem is NP-Hard. Our result is the first polynomial-time $(1+\varepsilon)$-approximation algorithm for an optimal motion planning problem involving two robots moving in a polygonal environment.
Coordination of Multiple Robots along Given Paths with Bounded Junction Complexity
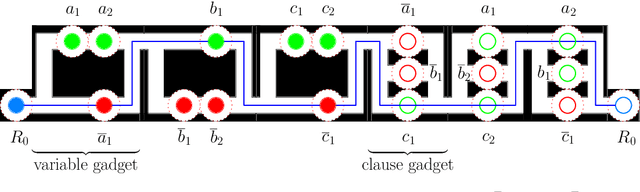
Mar 01, 2023Abstract:We study a fundamental NP-hard motion coordination problem for multi-robot/multi-agent systems: We are given a graph $G$ and set of agents, where each agent has a given directed path in $G$. Each agent is initially located on the first vertex of its path. At each time step an agent can move to the next vertex on its path, provided that the vertex is not occupied by another agent. The goal is to find a sequence of such moves along the given paths so that each reaches its target, or to report that no such sequence exists. The problem models guidepath-based transport systems, which is a pertinent abstraction for traffic in a variety of contemporary applications, ranging from train networks or Automated Guided Vehicles (AGVs) in factories, through computer game animations, to qubit transport in quantum computing. It also arises as a sub-problem in the more general multi-robot motion-planning problem. We provide a fine-grained tractability analysis of the problem by considering new assumptions and identifying minimal values of key parameters for which the problem remains NP-hard. Our analysis identifies a critical parameter called vertex multiplicity (VM), defined as the maximum number of paths passing through the same vertex. We show that a prevalent variant of the problem, which is equivalent to Sequential Resource Allocation (concerning deadlock prevention for concurrent processes), is NP-hard even when VM is 3. On the positive side, for VM $\le$ 2 we give an efficient algorithm that iteratively resolves cycles of blocking relations among agents. We also present a variant that is NP-hard when the VM is 2 even when $G$ is a 2D grid and each path lies in a single grid row or column. By studying highly distilled yet NP-hard variants, we deepen the understanding of what makes the problem intractable and thereby guide the search for efficient solutions under practical assumptions.
Multi-Robot Motion Planning for Unit Discs with Revolving Areas
Sep 30, 2022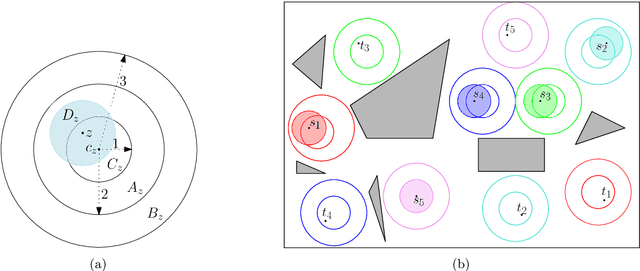
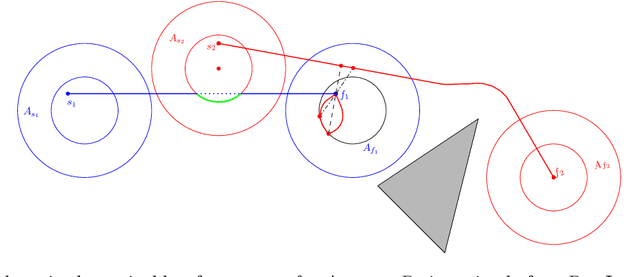
Abstract:We study the problem of motion planning for a collection of $n$ labeled unit disc robots in a polygonal environment. We assume that the robots have \emph{revolving areas} around their start and final positions: that each start and each final is contained in a radius $2$ disc lying in the free space, not necessarily concentric with the start or final position, which is free from other start or final positions. This assumption allows a \emph{weakly-monotone} motion plan, in which robots move according to an ordering as follows: during the turn of a robot $R$ in the ordering, it moves fully from its start to final position, while other robots do not leave their revolving areas. As $R$ passes through a revolving area, a robot $R'$ that is inside this area may move within the revolving area to avoid a collision. Notwithstanding the existence of a motion plan, we show that minimizing the total traveled distance in this setting, specifically even when the motion plan is restricted to be weakly-monotone, is APX-hard, ruling out any polynomial-time $(1+\epsilon)$-approximation algorithm. On the positive side, we present the first constant-factor approximation algorithm for computing a feasible weakly-monotone motion plan. The total distance traveled by the robots is within an $O(1)$ factor of that of the optimal motion plan, which need not be weakly monotone. Our algorithm extends to an online setting in which the polygonal environment is fixed but the initial and final positions of robots are specified in an online manner. Finally, we observe that the overhead in the overall cost that we add while editing the paths to avoid robot-robot collision can vary significantly depending on the ordering we chose. Finding the best ordering in this respect is known to be NP-hard, and we provide a polynomial time $O(\log n \log \log n)$-approximation algorithm for this problem.
Localization with Few Distance Measurements
Sep 11, 2022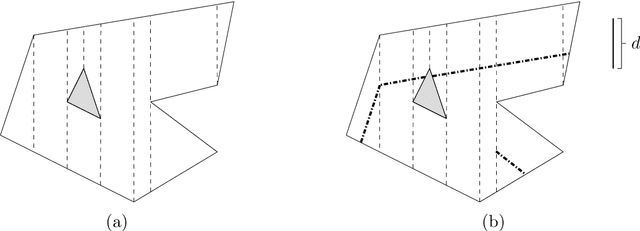
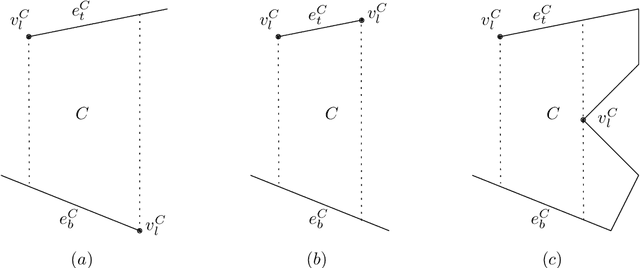
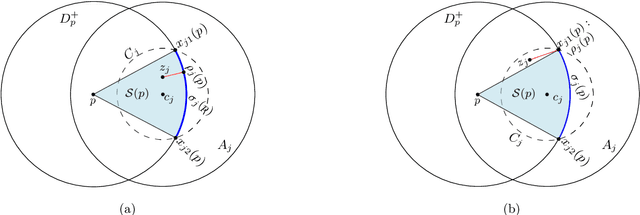
Abstract:Given a polygon $W$, a depth sensor placed at point $p=(x,y)$ inside $W$ and oriented in direction $\theta$ measures the distance $d=h(x,y,\theta)$ between $p$ and the closest point on the boundary of $W$ along a ray emanating from $p$ in direction $\theta$. We study the following problem: Give a polygon $W$, possibly with holes, with $n$ vertices, preprocess it such that given a query real value $d\geq 0$, one can efficiently compute the preimage $h^{-1}(d)$, namely determine all the possible poses (positions and orientations) of a depth sensor placed in $W$ that would yield the reading $d$. We employ a decomposition of $W\times S^1$, which is an extension of the celebrated trapezoidal decomposition, and which we call rotational trapezoidal decomposition and present an efficient data structure, which computes the preimage in an output-sensitive fashion relative to this decomposition: if $k$ cells of the decomposition contribute to the final result, we will report them in $O(k+1)$ time, after $O(n^2\log n)$ preprocessing time and using $O(n^2)$ storage space. We also analyze the shape of the projection of the preimage onto the polygon $W$; this projection describes the portion of $W$ where the sensor could have been placed. Furthermore, we obtain analogous results for the more useful case (narrowing down the set of possible poses), where the sensor performs two depth measurement from the same point $p$, one in direction $\theta$ and the other in direction $\theta+\pi$. While localizations problems in robotics are often carried out by exploring the full visibility polygon of a sensor placed at a fixed point of the environment, the approach that we propose here opens the door to sufficing with only few depth measurements, which is advantageous as it allows for usage of inexpensive sensors and could also lead to savings in storage and communication costs.
Unlabeled Multi-Robot Motion Planning with Tighter Separation Bounds
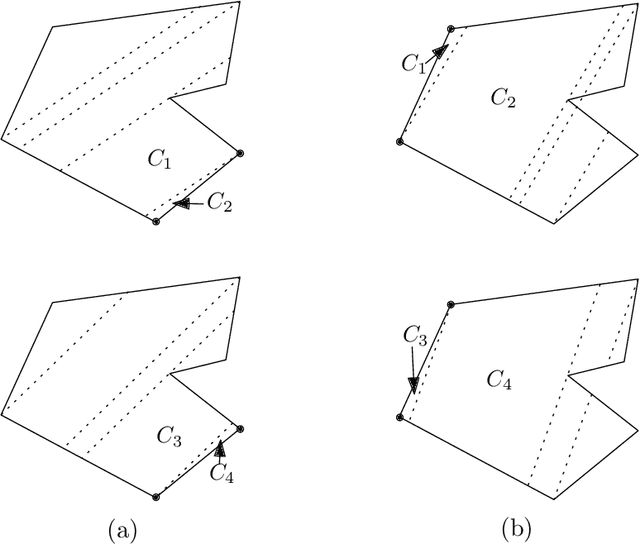
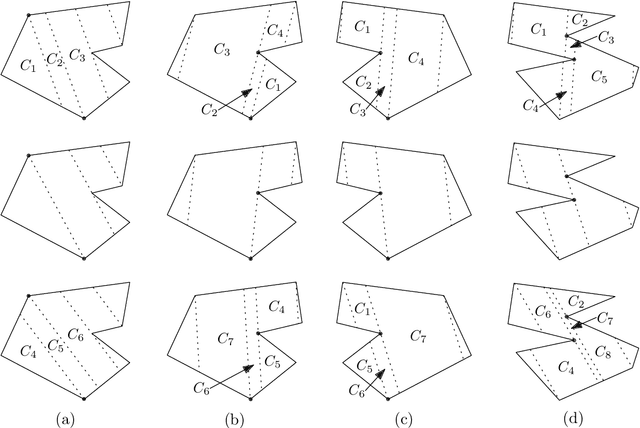
May 16, 2022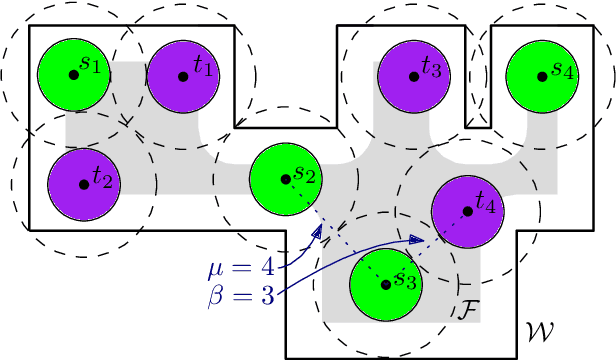
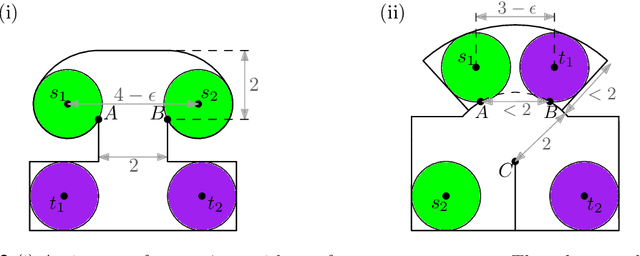
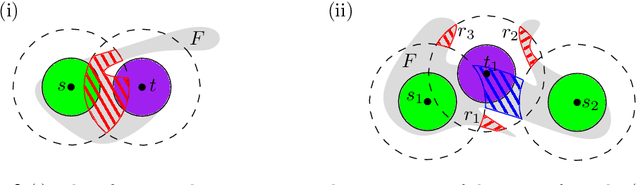
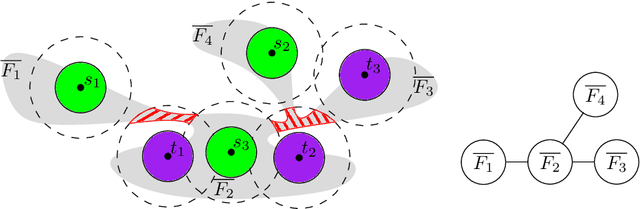
Abstract:We consider the unlabeled motion-planning problem of $m$ unit-disc robots moving in a simple polygonal workspace of $n$ edges. The goal is to find a motion plan that moves the robots to a given set of $m$ target positions. For the unlabeled variant, it does not matter which robot reaches which target position as long as all target positions are occupied in the end. If the workspace has narrow passages such that the robots cannot fit through them, then the free configuration space, representing all possible unobstructed positions of the robots, will consist of multiple connected components. Even if in each component of the free space the number of targets matches the number of start positions, the motion-planning problem does not always have a solution when the robots and their targets are positioned very densely. In this paper, we prove tight bounds on how much separation between start and target positions is necessary to always guarantee a solution. Moreover, we describe an algorithm that always finds a solution in time $O(n \log n + mn + m^2)$ if the separation bounds are met. Specifically, we prove that the following separation is sufficient: any two start positions are at least distance $4$ apart, any two target positions are at least distance $4$ apart, and any pair of a start and a target positions is at least distance $3$ apart. We further show that when the free space consists of a single connected component, the separation between start and target positions is not necessary.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge