Unlabeled Multi-Robot Motion Planning with Tighter Separation Bounds

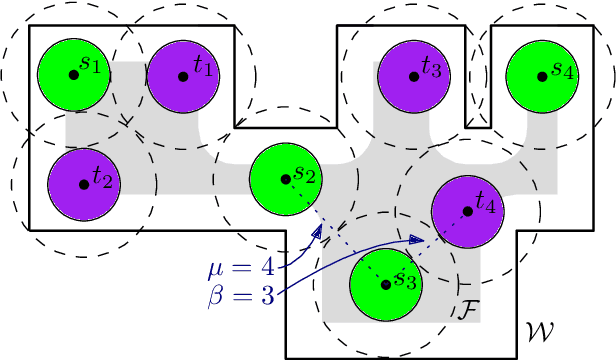
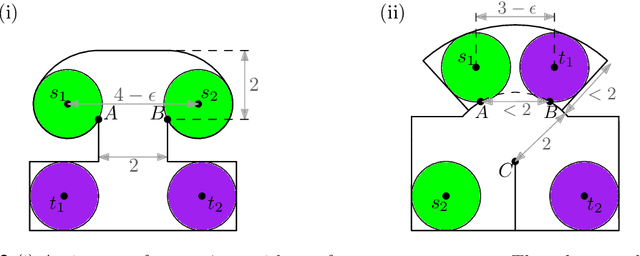
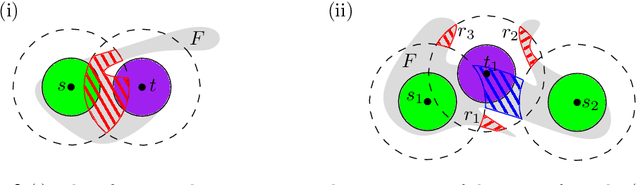
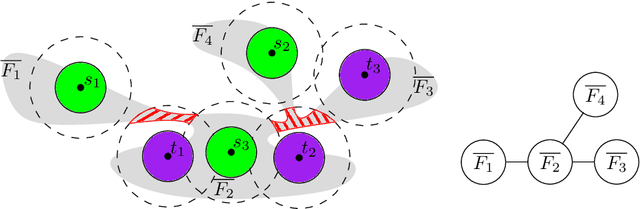
We consider the unlabeled motion-planning problem of $m$ unit-disc robots moving in a simple polygonal workspace of $n$ edges. The goal is to find a motion plan that moves the robots to a given set of $m$ target positions. For the unlabeled variant, it does not matter which robot reaches which target position as long as all target positions are occupied in the end. If the workspace has narrow passages such that the robots cannot fit through them, then the free configuration space, representing all possible unobstructed positions of the robots, will consist of multiple connected components. Even if in each component of the free space the number of targets matches the number of start positions, the motion-planning problem does not always have a solution when the robots and their targets are positioned very densely. In this paper, we prove tight bounds on how much separation between start and target positions is necessary to always guarantee a solution. Moreover, we describe an algorithm that always finds a solution in time $O(n \log n + mn + m^2)$ if the separation bounds are met. Specifically, we prove that the following separation is sufficient: any two start positions are at least distance $4$ apart, any two target positions are at least distance $4$ apart, and any pair of a start and a target positions is at least distance $3$ apart. We further show that when the free space consists of a single connected component, the separation between start and target positions is not necessary.

On Cyclic Solutions to the Min-Max Latency Multi-Robot Patrolling Problem

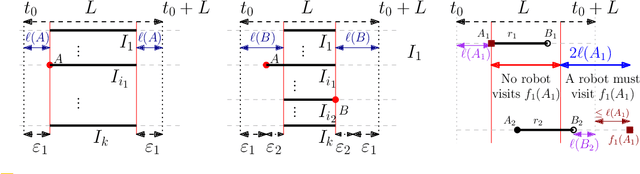
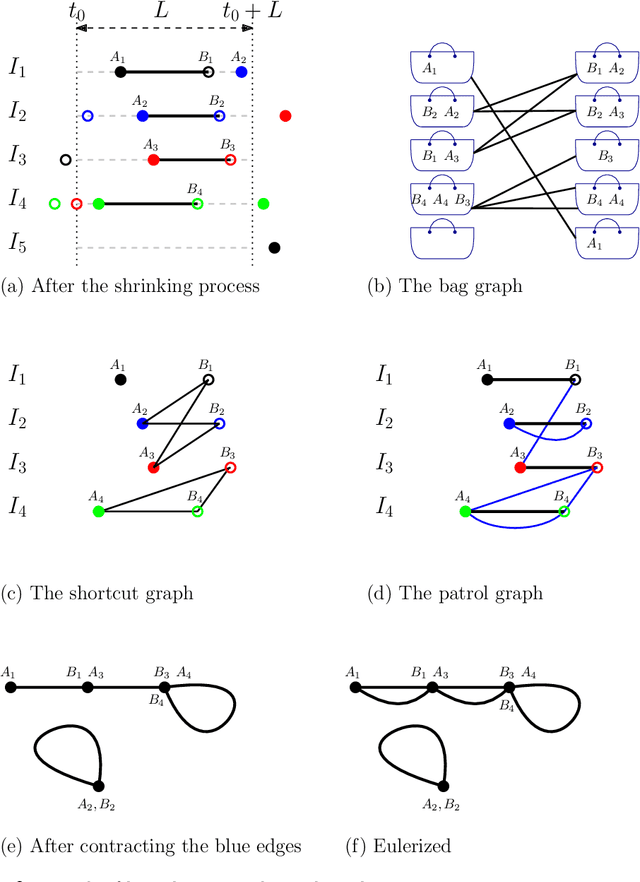
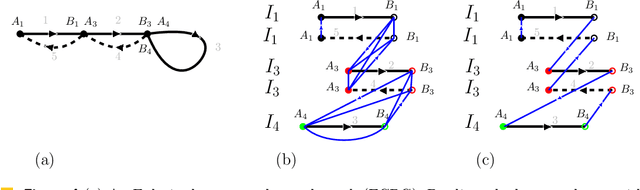
We consider the following surveillance problem: Given a set $P$ of $n$ sites in a metric space and a set of $k$ robots with the same maximum speed, compute a patrol schedule of minimum latency for the robots. Here a patrol schedule specifies for each robot an infinite sequence of sites to visit (in the given order) and the latency $L$ of a schedule is the maximum latency of any site, where the latency of a site $s$ is the supremum of the lengths of the time intervals between consecutive visits to $s$. When $k=1$ the problem is equivalent to the travelling salesman problem (TSP) and thus it is NP-hard. We have two main results. We consider cyclic solutions in which the set of sites must be partitioned into $\ell$ groups, for some~$\ell \leq k$, and each group is assigned a subset of the robots that move along the travelling salesman tour of the group at equal distance from each other. Our first main result is that approximating the optimal latency of the class of cyclic solutions can be reduced to approximating the optimal travelling salesman tour on some input, with only a $1+\varepsilon$ factor loss in the approximation factor and an $O\left(\left( k/\varepsilon \right)^k\right)$ factor loss in the runtime, for any $\varepsilon >0$. Our second main result shows that an optimal cyclic solution is a $2(1-1/k)$-approximation of the overall optimal solution. Note that for $k=2$ this implies that an optimal cyclic solution is optimal overall. The results have a number of consequences. For the Euclidean version of the problem, for instance, combining our results with known results on Euclidean TSP, yields a PTAS for approximating an optimal cyclic solution, and it yields a $(2(1-1/k)+\varepsilon)$-approximation of the optimal unrestricted solution. If the conjecture mentioned above is true, then our algorithm is actually a PTAS for the general problem in the Euclidean setting.

(k, l)-Medians Clustering of Trajectories Using Continuous Dynamic Time Warping

Due to the massively increasing amount of available geospatial data and the need to present it in an understandable way, clustering this data is more important than ever. As clusters might contain a large number of objects, having a representative for each cluster significantly facilitates understanding a clustering. Clustering methods relying on such representatives are called center-based. In this work we consider the problem of center-based clustering of trajectories. In this setting, the representative of a cluster is again a trajectory. To obtain a compact representation of the clusters and to avoid overfitting, we restrict the complexity of the representative trajectories by a parameter l. This restriction, however, makes discrete distance measures like dynamic time warping (DTW) less suited. There is recent work on center-based clustering of trajectories with a continuous distance measure, namely, the Fr\'echet distance. While the Fr\'echet distance allows for restriction of the center complexity, it can also be sensitive to outliers, whereas averaging-type distance measures, like DTW, are less so. To obtain a trajectory clustering algorithm that allows restricting center complexity and is more robust to outliers, we propose the usage of a continuous version of DTW as distance measure, which we call continuous dynamic time warping (CDTW). Our contribution is twofold: 1. To combat the lack of practical algorithms for CDTW, we develop an approximation algorithm that computes it. 2. We develop the first clustering algorithm under this distance measure and show a practical way to compute a center from a set of trajectories and subsequently iteratively improve it. To obtain insights into the results of clustering under CDTW on practical data, we conduct extensive experiments.

Approximation Algorithms for Multi-Robot Patrol-Scheduling with Min-Max Latency

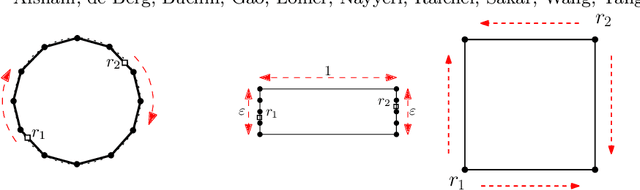
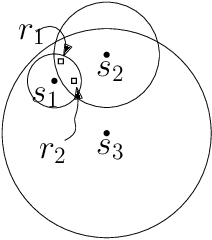
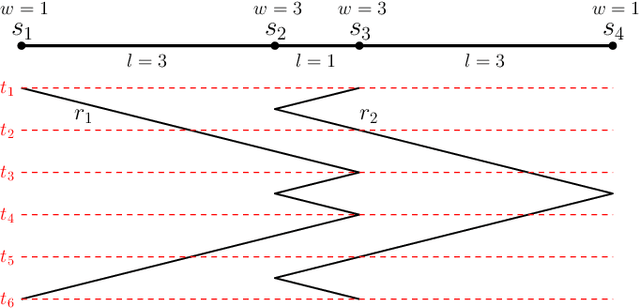
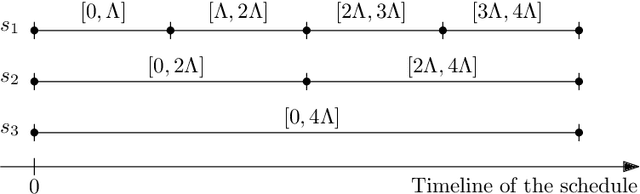
We consider the problem of finding patrol schedules for $k$ robots to visit a given set of $n$ sites in a metric space. Each robot has the same maximum speed and the goal is to minimize the weighted maximum latency of any site, where the latency of a site is defined as the maximum time duration between consecutive visits of that site. The problem is NP-hard, as it has the traveling salesman problem as a special case (when $k=1$ and all sites have the same weight). We present a polynomial-time algorithm with an approximation factor of $O(k^2 \log \frac{w_{\max}}{w_{\min}})$ to the optimal solution, where $w_{\max}$ and $w_{\min}$ are the maximum and minimum weight of the sites respectively. Further, we consider the special case where the sites are in 1D. When all sites have the same weight, we present a polynomial-time algorithm to solve the problem exactly. If the sites may have different weights, we present a $12$-approximate solution, which runs in polynomial time when the number of robots, $k$, is a constant.