Unlabeled Multi-Robot Motion Planning with Tighter Separation Bounds

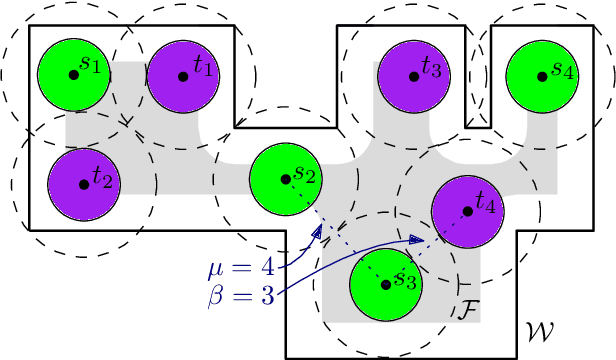
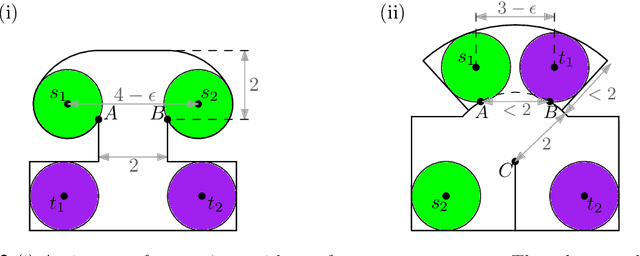
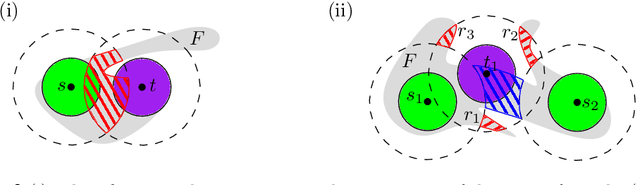
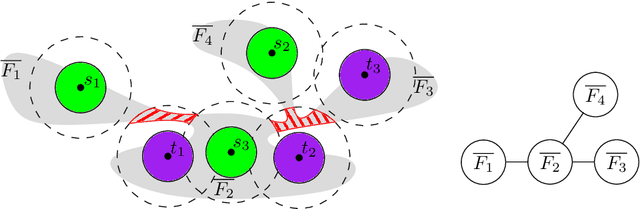
We consider the unlabeled motion-planning problem of $m$ unit-disc robots moving in a simple polygonal workspace of $n$ edges. The goal is to find a motion plan that moves the robots to a given set of $m$ target positions. For the unlabeled variant, it does not matter which robot reaches which target position as long as all target positions are occupied in the end. If the workspace has narrow passages such that the robots cannot fit through them, then the free configuration space, representing all possible unobstructed positions of the robots, will consist of multiple connected components. Even if in each component of the free space the number of targets matches the number of start positions, the motion-planning problem does not always have a solution when the robots and their targets are positioned very densely. In this paper, we prove tight bounds on how much separation between start and target positions is necessary to always guarantee a solution. Moreover, we describe an algorithm that always finds a solution in time $O(n \log n + mn + m^2)$ if the separation bounds are met. Specifically, we prove that the following separation is sufficient: any two start positions are at least distance $4$ apart, any two target positions are at least distance $4$ apart, and any pair of a start and a target positions is at least distance $3$ apart. We further show that when the free space consists of a single connected component, the separation between start and target positions is not necessary.

On Cyclic Solutions to the Min-Max Latency Multi-Robot Patrolling Problem

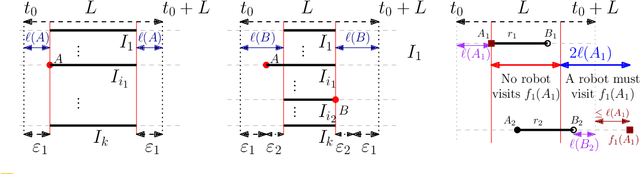
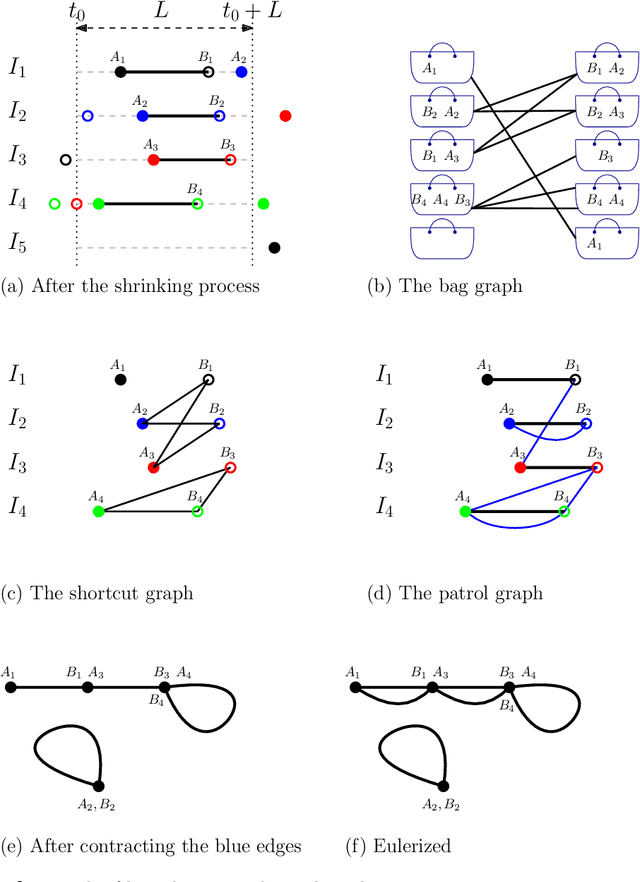
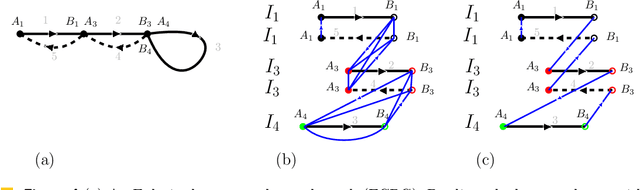
We consider the following surveillance problem: Given a set $P$ of $n$ sites in a metric space and a set of $k$ robots with the same maximum speed, compute a patrol schedule of minimum latency for the robots. Here a patrol schedule specifies for each robot an infinite sequence of sites to visit (in the given order) and the latency $L$ of a schedule is the maximum latency of any site, where the latency of a site $s$ is the supremum of the lengths of the time intervals between consecutive visits to $s$. When $k=1$ the problem is equivalent to the travelling salesman problem (TSP) and thus it is NP-hard. We have two main results. We consider cyclic solutions in which the set of sites must be partitioned into $\ell$ groups, for some~$\ell \leq k$, and each group is assigned a subset of the robots that move along the travelling salesman tour of the group at equal distance from each other. Our first main result is that approximating the optimal latency of the class of cyclic solutions can be reduced to approximating the optimal travelling salesman tour on some input, with only a $1+\varepsilon$ factor loss in the approximation factor and an $O\left(\left( k/\varepsilon \right)^k\right)$ factor loss in the runtime, for any $\varepsilon >0$. Our second main result shows that an optimal cyclic solution is a $2(1-1/k)$-approximation of the overall optimal solution. Note that for $k=2$ this implies that an optimal cyclic solution is optimal overall. The results have a number of consequences. For the Euclidean version of the problem, for instance, combining our results with known results on Euclidean TSP, yields a PTAS for approximating an optimal cyclic solution, and it yields a $(2(1-1/k)+\varepsilon)$-approximation of the optimal unrestricted solution. If the conjecture mentioned above is true, then our algorithm is actually a PTAS for the general problem in the Euclidean setting.

Efficient Multi-Robot Motion Planning for Unlabeled Discs in Simple Polygons

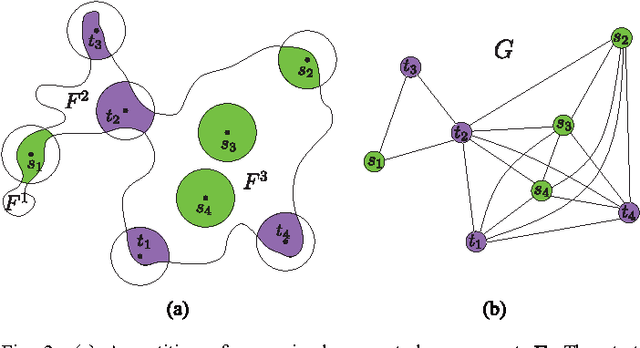
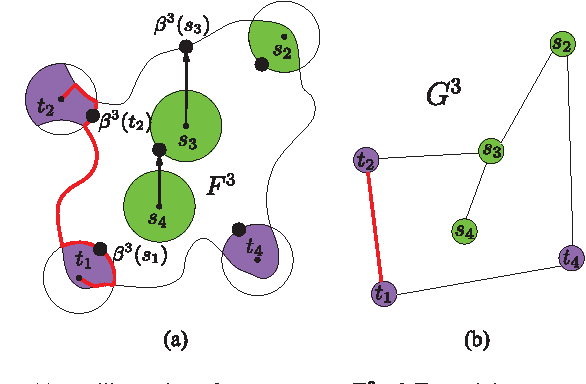
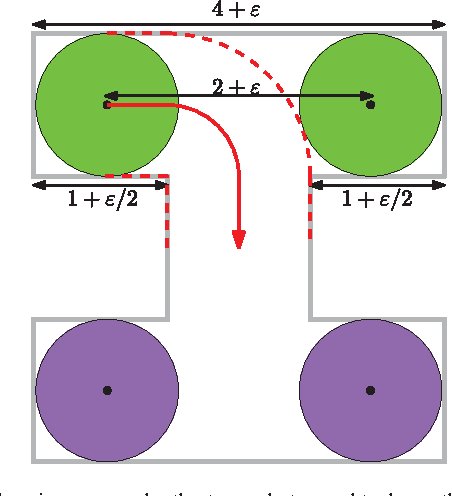
We consider the following motion-planning problem: we are given $m$ unit discs in a simple polygon with $n$ vertices, each at their own start position, and we want to move the discs to a given set of $m$ target positions. Contrary to the standard (labeled) version of the problem, each disc is allowed to be moved to any target position, as long as in the end every target position is occupied. We show that this unlabeled version of the problem can be solved in $O(n\log n+mn+m^2)$ time, assuming that the start and target positions are at least some minimal distance from each other. This is in sharp contrast to the standard (labeled) and more general multi-robot motion-planning problem for discs moving in a simple polygon, which is known to be strongly NP-hard.