On Cyclic Solutions to the Min-Max Latency Multi-Robot Patrolling Problem

We consider the following surveillance problem: Given a set $P$ of $n$ sites in a metric space and a set of $k$ robots with the same maximum speed, compute a patrol schedule of minimum latency for the robots. Here a patrol schedule specifies for each robot an infinite sequence of sites to visit (in the given order) and the latency $L$ of a schedule is the maximum latency of any site, where the latency of a site $s$ is the supremum of the lengths of the time intervals between consecutive visits to $s$. When $k=1$ the problem is equivalent to the travelling salesman problem (TSP) and thus it is NP-hard. We have two main results. We consider cyclic solutions in which the set of sites must be partitioned into $\ell$ groups, for some~$\ell \leq k$, and each group is assigned a subset of the robots that move along the travelling salesman tour of the group at equal distance from each other. Our first main result is that approximating the optimal latency of the class of cyclic solutions can be reduced to approximating the optimal travelling salesman tour on some input, with only a $1+\varepsilon$ factor loss in the approximation factor and an $O\left(\left( k/\varepsilon \right)^k\right)$ factor loss in the runtime, for any $\varepsilon >0$. Our second main result shows that an optimal cyclic solution is a $2(1-1/k)$-approximation of the overall optimal solution. Note that for $k=2$ this implies that an optimal cyclic solution is optimal overall. The results have a number of consequences. For the Euclidean version of the problem, for instance, combining our results with known results on Euclidean TSP, yields a PTAS for approximating an optimal cyclic solution, and it yields a $(2(1-1/k)+\varepsilon)$-approximation of the optimal unrestricted solution. If the conjecture mentioned above is true, then our algorithm is actually a PTAS for the general problem in the Euclidean setting.

How can classical multidimensional scaling go wrong?

Given a matrix $D$ describing the pairwise dissimilarities of a data set, a common task is to embed the data points into Euclidean space. The classical multidimensional scaling (cMDS) algorithm is a widespread method to do this. However, theoretical analysis of the robustness of the algorithm and an in-depth analysis of its performance on non-Euclidean metrics is lacking. In this paper, we derive a formula, based on the eigenvalues of a matrix obtained from $D$, for the Frobenius norm of the difference between $D$ and the metric $D_{\text{cmds}}$ returned by cMDS. This error analysis leads us to the conclusion that when the derived matrix has a significant number of negative eigenvalues, then $\|D-D_{\text{cmds}}\|_F$, after initially decreasing, will eventually increase as we increase the dimension. Hence, counterintuitively, the quality of the embedding degrades as we increase the dimension. We empirically verify that the Frobenius norm increases as we increase the dimension for a variety of non-Euclidean metrics. We also show on several benchmark datasets that this degradation in the embedding results in the classification accuracy of both simple (e.g., 1-nearest neighbor) and complex (e.g., multi-layer neural nets) classifiers decreasing as we increase the embedding dimension. Finally, our analysis leads us to a new efficiently computable algorithm that returns a matrix $D_l$ that is at least as close to the original distances as $D_t$ (the Euclidean metric closest in $\ell_2$ distance). While $D_l$ is not metric, when given as input to cMDS instead of $D$, it empirically results in solutions whose distance to $D$ does not increase when we increase the dimension and the classification accuracy degrades less than the cMDS solution.

Approximation Algorithms for Multi-Robot Patrol-Scheduling with Min-Max Latency

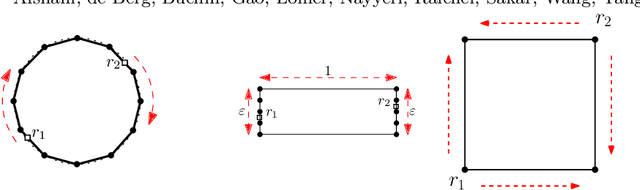
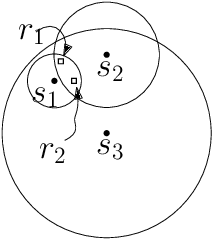
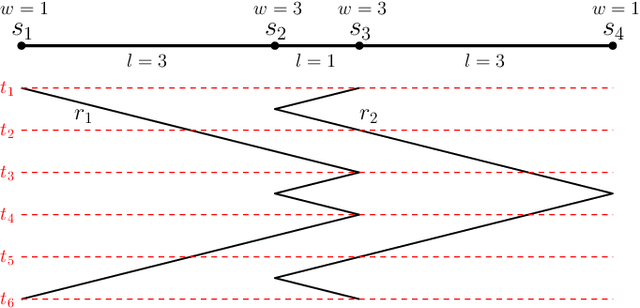
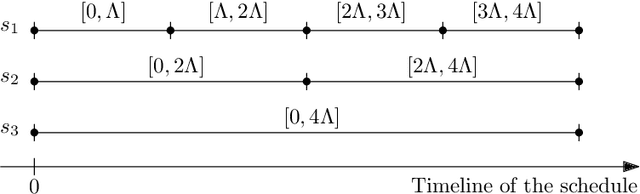
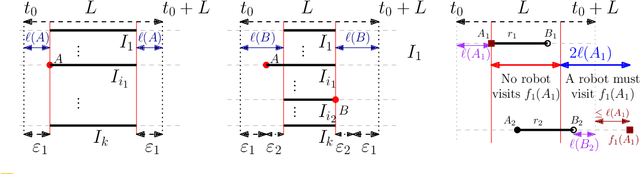
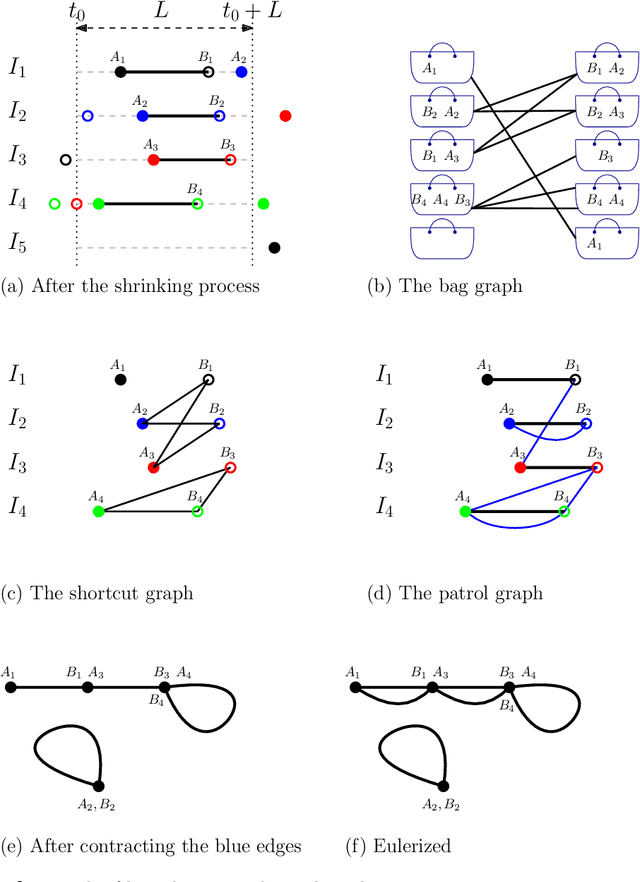
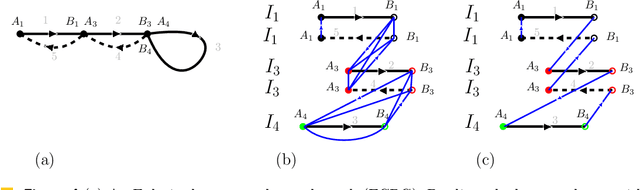
We consider the problem of finding patrol schedules for $k$ robots to visit a given set of $n$ sites in a metric space. Each robot has the same maximum speed and the goal is to minimize the weighted maximum latency of any site, where the latency of a site is defined as the maximum time duration between consecutive visits of that site. The problem is NP-hard, as it has the traveling salesman problem as a special case (when $k=1$ and all sites have the same weight). We present a polynomial-time algorithm with an approximation factor of $O(k^2 \log \frac{w_{\max}}{w_{\min}})$ to the optimal solution, where $w_{\max}$ and $w_{\min}$ are the maximum and minimum weight of the sites respectively. Further, we consider the special case where the sites are in 1D. When all sites have the same weight, we present a polynomial-time algorithm to solve the problem exactly. If the sites may have different weights, we present a $12$-approximate solution, which runs in polynomial time when the number of robots, $k$, is a constant.

Sparse Approximation via Generating Point Sets

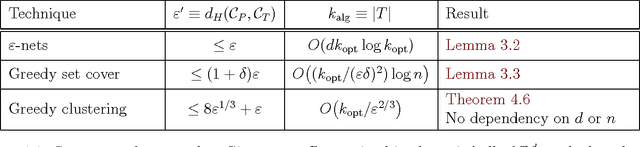
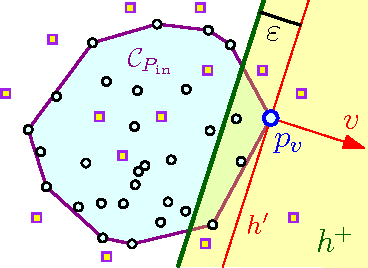
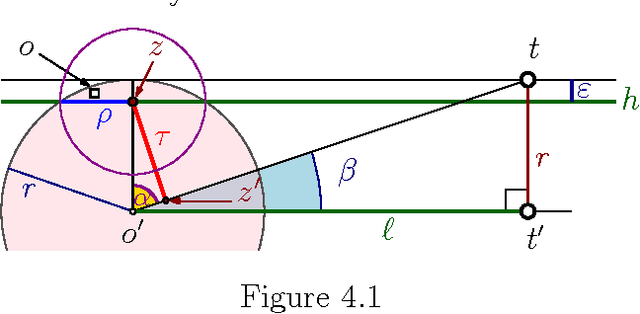
$ \newcommand{\kalg}{{k_{\mathrm{alg}}}} \newcommand{\kopt}{{k_{\mathrm{opt}}}} \newcommand{\algset}{{T}} \renewcommand{\Re}{\mathbb{R}} \newcommand{\eps}{\varepsilon} \newcommand{\pth}[2][\!]{#1\left({#2}\right)} \newcommand{\npoints}{n} \newcommand{\ballD}{\mathsf{b}} \newcommand{\dataset}{{P}} $ For a set $\dataset$ of $\npoints$ points in the unit ball $\ballD \subseteq \Re^d$, consider the problem of finding a small subset $\algset \subseteq \dataset$ such that its convex-hull $\eps$-approximates the convex-hull of the original set. We present an efficient algorithm to compute such a $\eps'$-approximation of size $\kalg$, where $\eps'$ is function of $\eps$, and $\kalg$ is a function of the minimum size $\kopt$ of such an $\eps$-approximation. Surprisingly, there is no dependency on the dimension $d$ in both bounds. Furthermore, every point of $\dataset$ can be $\eps$-approximated by a convex-combination of points of $\algset$ that is $O(1/\eps^2)$-sparse. Our result can be viewed as a method for sparse, convex autoencoding: approximately representing the data in a compact way using sparse combinations of a small subset $\algset$ of the original data. The new algorithm can be kernelized, and it preserves sparsity in the original input.