Approximating Metric Magnitude of Point Sets

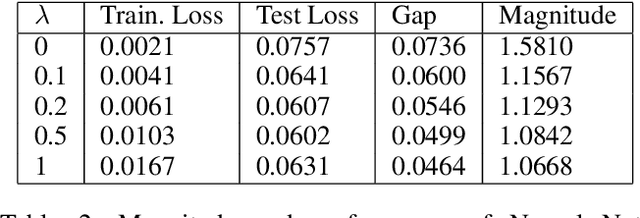
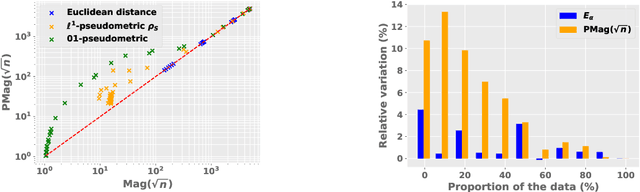
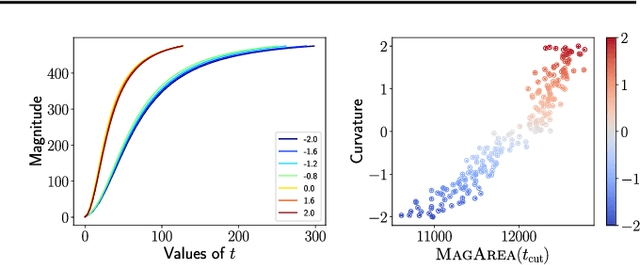
Metric magnitude is a measure of the "size" of point clouds with many desirable geometric properties. It has been adapted to various mathematical contexts and recent work suggests that it can enhance machine learning and optimization algorithms. But its usability is limited due to the computational cost when the dataset is large or when the computation must be carried out repeatedly (e.g. in model training). In this paper, we study the magnitude computation problem, and show efficient ways of approximating it. We show that it can be cast as a convex optimization problem, but not as a submodular optimization. The paper describes two new algorithms - an iterative approximation algorithm that converges fast and is accurate, and a subset selection method that makes the computation even faster. It has been previously proposed that magnitude of model sequences generated during stochastic gradient descent is correlated to generalization gap. Extension of this result using our more scalable algorithms shows that longer sequences in fact bear higher correlations. We also describe new applications of magnitude in machine learning - as an effective regularizer for neural network training, and as a novel clustering criterion.

Topological Generalization Bounds for Discrete-Time Stochastic Optimization Algorithms

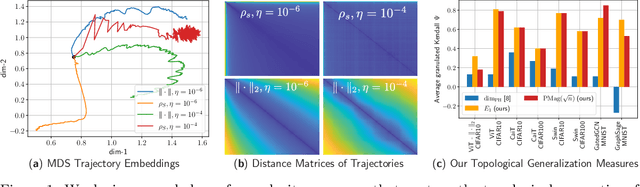
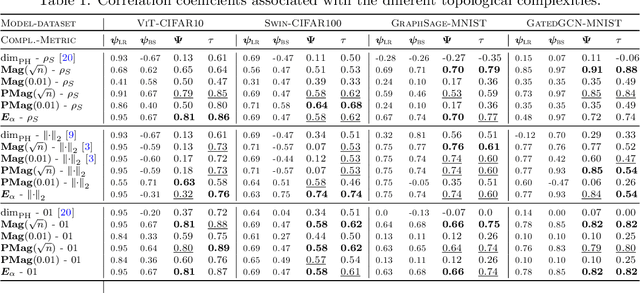
We present a novel set of rigorous and computationally efficient topology-based complexity notions that exhibit a strong correlation with the generalization gap in modern deep neural networks (DNNs). DNNs show remarkable generalization properties, yet the source of these capabilities remains elusive, defying the established statistical learning theory. Recent studies have revealed that properties of training trajectories can be indicative of generalization. Building on this insight, state-of-the-art methods have leveraged the topology of these trajectories, particularly their fractal dimension, to quantify generalization. Most existing works compute this quantity by assuming continuous- or infinite-time training dynamics, complicating the development of practical estimators capable of accurately predicting generalization without access to test data. In this paper, we respect the discrete-time nature of training trajectories and investigate the underlying topological quantities that can be amenable to topological data analysis tools. This leads to a new family of reliable topological complexity measures that provably bound the generalization error, eliminating the need for restrictive geometric assumptions. These measures are computationally friendly, enabling us to propose simple yet effective algorithms for computing generalization indices. Moreover, our flexible framework can be extended to different domains, tasks, and architectures. Our experimental results demonstrate that our new complexity measures correlate highly with generalization error in industry-standards architectures such as transformers and deep graph networks. Our approach consistently outperforms existing topological bounds across a wide range of datasets, models, and optimizers, highlighting the practical relevance and effectiveness of our complexity measures.

Metric Space Magnitude for Evaluating Unsupervised Representation Learning

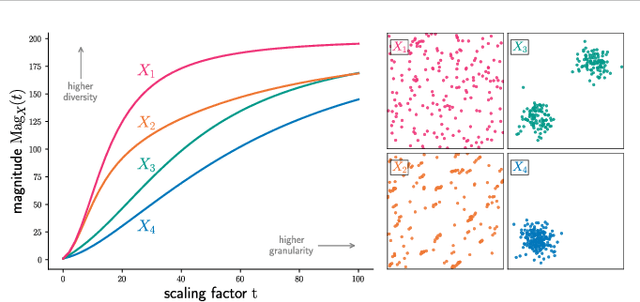
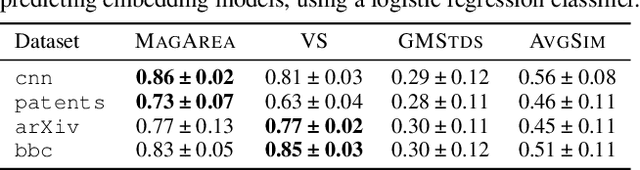
The magnitude of a metric space was recently established as a novel invariant, providing a measure of the `effective size' of a space across multiple scales. By capturing both geometrical and topological properties of data, magnitude is poised to address challenges in unsupervised representation learning tasks. We formalise a novel notion of dissimilarity between magnitude functions of finite metric spaces and use them to derive a quality measure for dimensionality reduction tasks. Our measure is provably stable under perturbations of the data, can be efficiently calculated, and enables a rigorous multi-scale comparison of embeddings. We show the utility of our measure in an experimental suite that comprises different domains and tasks, including the comparison of data visualisations.

Inference and Interference: The Role of Clipping, Pruning and Loss Landscapes in Differentially Private Stochastic Gradient Descent

Differentially private stochastic gradient descent (DP-SGD) is known to have poorer training and test performance on large neural networks, compared to ordinary stochastic gradient descent (SGD). In this paper, we perform a detailed study and comparison of the two processes and unveil several new insights. By comparing the behavior of the two processes separately in early and late epochs, we find that while DP-SGD makes slower progress in early stages, it is the behavior in the later stages that determines the end result. This separate analysis of the clipping and noise addition steps of DP-SGD shows that while noise introduces errors to the process, gradient descent can recover from these errors when it is not clipped, and clipping appears to have a larger impact than noise. These effects are amplified in higher dimensions (large neural networks), where the loss basin occupies a lower dimensional space. We argue theoretically and using extensive experiments that magnitude pruning can be a suitable dimension reduction technique in this regard, and find that heavy pruning can improve the test accuracy of DPSGD.

Accelerated Shapley Value Approximation for Data Evaluation

Data valuation has found various applications in machine learning, such as data filtering, efficient learning and incentives for data sharing. The most popular current approach to data valuation is the Shapley value. While popular for its various applications, Shapley value is computationally expensive even to approximate, as it requires repeated iterations of training models on different subsets of data. In this paper we show that the Shapley value of data points can be approximated more efficiently by leveraging the structural properties of machine learning problems. We derive convergence guarantees on the accuracy of the approximate Shapley value for different learning settings including Stochastic Gradient Descent with convex and non-convex loss functions. Our analysis suggests that in fact models trained on small subsets are more important in the context of data valuation. Based on this idea, we describe $\delta$-Shapley -- a strategy of only using small subsets for the approximation. Experiments show that this approach preserves approximate value and rank of data, while achieving speedup of up to 9.9x. In pre-trained networks the approach is found to bring more efficiency in terms of accurate evaluation using small subsets.

Machine learning and Topological data analysis identify unique features of human papillae in 3D scans

The tongue surface houses a range of papillae that are integral to the mechanics and chemistry of taste and textural sensation. Although gustatory function of papillae is well investigated, the uniqueness of papillae within and across individuals remains elusive. Here, we present the first machine learning framework on 3D microscopic scans of human papillae (n = 2092), uncovering the uniqueness of geometric and topological features of papillae. The finer differences in shapes of papillae are investigated computationally based on a number of features derived from discrete differential geometry and computational topology. Interpretable machine learning techniques show that persistent homology features of the papillae shape are the most effective in predicting the biological variables. Models trained on these features with small volumes of data samples predict the type of papillae with an accuracy of 85%. The papillae type classification models can map the spatial arrangement of filiform and fungiform papillae on a surface. Remarkably, the papillae are found to be distinctive across individuals and an individual can be identified with an accuracy of 48% among the 15 participants from a single papillae. Collectively, this is the first unprecedented evidence demonstrating that tongue papillae can serve as a unique identifier inspiring new research direction for food preferences and oral diagnostics.

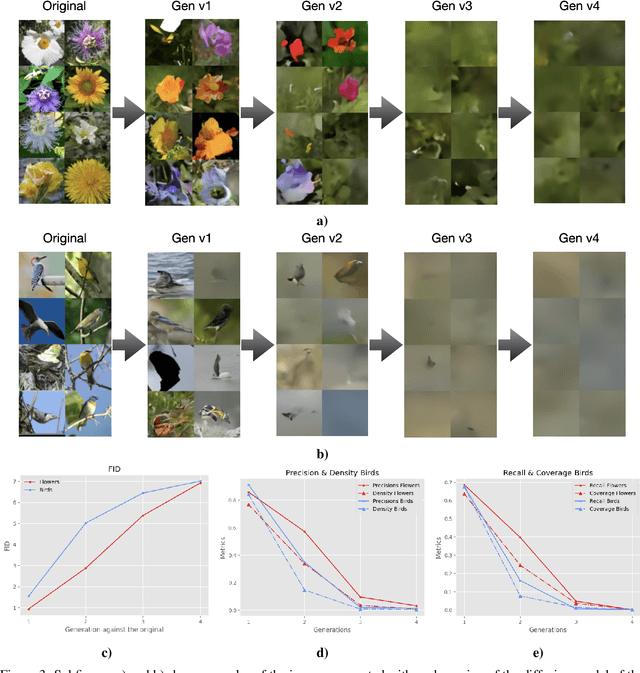
Towards Understanding the Interplay of Generative Artificial Intelligence and the Internet

The rapid adoption of generative Artificial Intelligence (AI) tools that can generate realistic images or text, such as DALL-E, MidJourney, or ChatGPT, have put the societal impacts of these technologies at the center of public debate. These tools are possible due to the massive amount of data (text and images) that is publicly available through the Internet. At the same time, these generative AI tools become content creators that are already contributing to the data that is available to train future models. Therefore, future versions of generative AI tools will be trained with a mix of human-created and AI-generated content, causing a potential feedback loop between generative AI and public data repositories. This interaction raises many questions: how will future versions of generative AI tools behave when trained on a mixture of real and AI generated data? Will they evolve and improve with the new data sets or on the contrary will they degrade? Will evolution introduce biases or reduce diversity in subsequent generations of generative AI tools? What are the societal implications of the possible degradation of these models? Can we mitigate the effects of this feedback loop? In this document, we explore the effect of this interaction and report some initial results using simple diffusion models trained with various image datasets. Our results show that the quality and diversity of the generated images can degrade over time suggesting that incorporating AI-created data can have undesired effects on future versions of generative models.

Metric Space Magnitude and Generalisation in Neural Networks

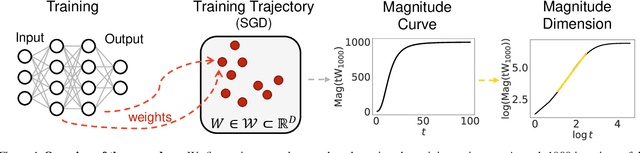
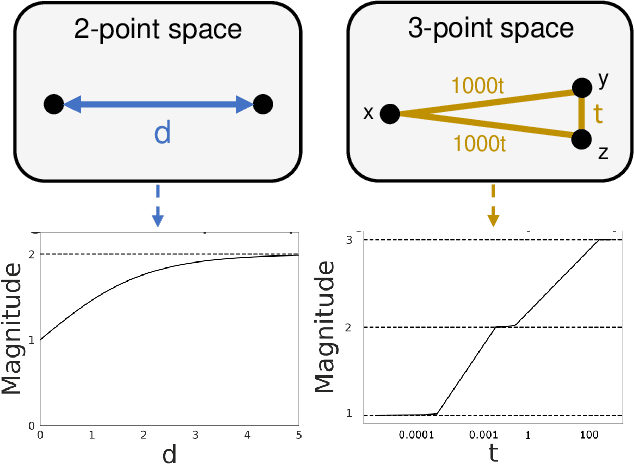
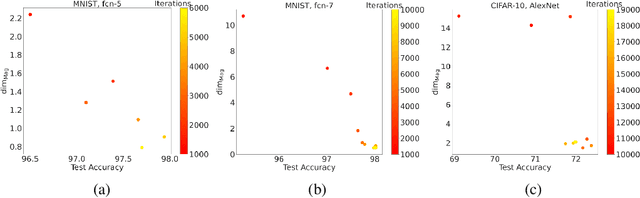
Deep learning models have seen significant successes in numerous applications, but their inner workings remain elusive. The purpose of this work is to quantify the learning process of deep neural networks through the lens of a novel topological invariant called magnitude. Magnitude is an isometry invariant; its properties are an active area of research as it encodes many known invariants of a metric space. We use magnitude to study the internal representations of neural networks and propose a new method for determining their generalisation capabilities. Moreover, we theoretically connect magnitude dimension and the generalisation error, and demonstrate experimentally that the proposed framework can be a good indicator of the latter.

Combining Generative Artificial Intelligence (AI) and the Internet: Heading towards Evolution or Degradation?

In the span of a few months, generative Artificial Intelligence (AI) tools that can generate realistic images or text have taken the Internet by storm, making them one of the technologies with fastest adoption ever. Some of these generative AI tools such as DALL-E, MidJourney, or ChatGPT have gained wide public notoriety. Interestingly, these tools are possible because of the massive amount of data (text and images) available on the Internet. The tools are trained on massive data sets that are scraped from Internet sites. And now, these generative AI tools are creating massive amounts of new data that are being fed into the Internet. Therefore, future versions of generative AI tools will be trained with Internet data that is a mix of original and AI-generated data. As time goes on, a mixture of original data and data generated by different versions of AI tools will populate the Internet. This raises a few intriguing questions: how will future versions of generative AI tools behave when trained on a mixture of real and AI generated data? Will they evolve with the new data sets or degenerate? Will evolution introduce biases in subsequent generations of generative AI tools? In this document, we explore these questions and report some very initial simulation results using a simple image-generation AI tool. These results suggest that the quality of the generated images degrades as more AI-generated data is used for training thus suggesting that generative AI may degenerate. Although these results are preliminary and cannot be generalised without further study, they serve to illustrate the potential issues of the interaction between generative AI and the Internet.

Differentially Private Shapley Values for Data Evaluation

The Shapley value has been proposed as a solution to many applications in machine learning, including for equitable valuation of data. Shapley values are computationally expensive and involve the entire dataset. The query for a point's Shapley value can also compromise the statistical privacy of other data points. We observe that in machine learning problems such as empirical risk minimization, and in many learning algorithms (such as those with uniform stability), a diminishing returns property holds, where marginal benefit per data point decreases rapidly with data sample size. Based on this property, we propose a new stratified approximation method called the Layered Shapley Algorithm. We prove that this method operates on small (O(\polylog(n))) random samples of data and small sized ($O(\log n)$) coalitions to achieve the results with guaranteed probabilistic accuracy, and can be modified to incorporate differential privacy. Experimental results show that the algorithm correctly identifies high-value data points that improve validation accuracy, and that the differentially private evaluations preserve approximate ranking of data.