Inference and Interference: The Role of Clipping, Pruning and Loss Landscapes in Differentially Private Stochastic Gradient Descent

Differentially private stochastic gradient descent (DP-SGD) is known to have poorer training and test performance on large neural networks, compared to ordinary stochastic gradient descent (SGD). In this paper, we perform a detailed study and comparison of the two processes and unveil several new insights. By comparing the behavior of the two processes separately in early and late epochs, we find that while DP-SGD makes slower progress in early stages, it is the behavior in the later stages that determines the end result. This separate analysis of the clipping and noise addition steps of DP-SGD shows that while noise introduces errors to the process, gradient descent can recover from these errors when it is not clipped, and clipping appears to have a larger impact than noise. These effects are amplified in higher dimensions (large neural networks), where the loss basin occupies a lower dimensional space. We argue theoretically and using extensive experiments that magnitude pruning can be a suitable dimension reduction technique in this regard, and find that heavy pruning can improve the test accuracy of DPSGD.

Accelerated Shapley Value Approximation for Data Evaluation

Data valuation has found various applications in machine learning, such as data filtering, efficient learning and incentives for data sharing. The most popular current approach to data valuation is the Shapley value. While popular for its various applications, Shapley value is computationally expensive even to approximate, as it requires repeated iterations of training models on different subsets of data. In this paper we show that the Shapley value of data points can be approximated more efficiently by leveraging the structural properties of machine learning problems. We derive convergence guarantees on the accuracy of the approximate Shapley value for different learning settings including Stochastic Gradient Descent with convex and non-convex loss functions. Our analysis suggests that in fact models trained on small subsets are more important in the context of data valuation. Based on this idea, we describe $\delta$-Shapley -- a strategy of only using small subsets for the approximation. Experiments show that this approach preserves approximate value and rank of data, while achieving speedup of up to 9.9x. In pre-trained networks the approach is found to bring more efficiency in terms of accurate evaluation using small subsets.

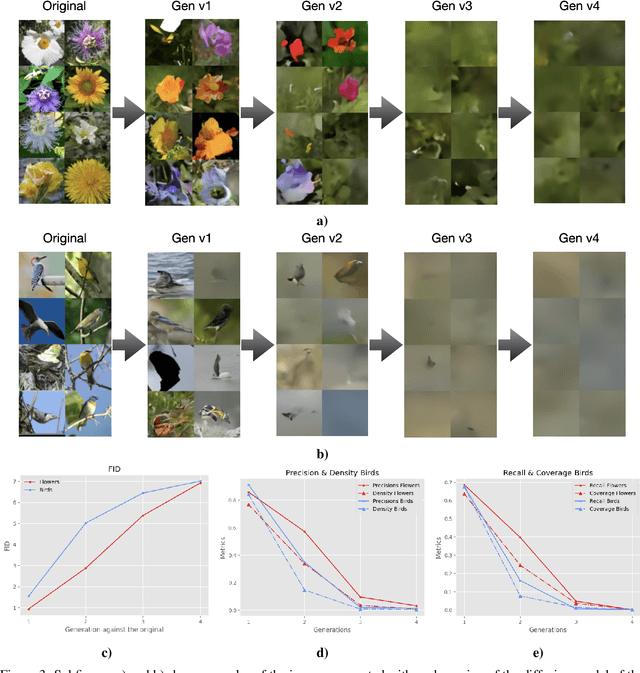
Towards Understanding the Interplay of Generative Artificial Intelligence and the Internet

The rapid adoption of generative Artificial Intelligence (AI) tools that can generate realistic images or text, such as DALL-E, MidJourney, or ChatGPT, have put the societal impacts of these technologies at the center of public debate. These tools are possible due to the massive amount of data (text and images) that is publicly available through the Internet. At the same time, these generative AI tools become content creators that are already contributing to the data that is available to train future models. Therefore, future versions of generative AI tools will be trained with a mix of human-created and AI-generated content, causing a potential feedback loop between generative AI and public data repositories. This interaction raises many questions: how will future versions of generative AI tools behave when trained on a mixture of real and AI generated data? Will they evolve and improve with the new data sets or on the contrary will they degrade? Will evolution introduce biases or reduce diversity in subsequent generations of generative AI tools? What are the societal implications of the possible degradation of these models? Can we mitigate the effects of this feedback loop? In this document, we explore the effect of this interaction and report some initial results using simple diffusion models trained with various image datasets. Our results show that the quality and diversity of the generated images can degrade over time suggesting that incorporating AI-created data can have undesired effects on future versions of generative models.

Combining Generative Artificial Intelligence (AI) and the Internet: Heading towards Evolution or Degradation?

In the span of a few months, generative Artificial Intelligence (AI) tools that can generate realistic images or text have taken the Internet by storm, making them one of the technologies with fastest adoption ever. Some of these generative AI tools such as DALL-E, MidJourney, or ChatGPT have gained wide public notoriety. Interestingly, these tools are possible because of the massive amount of data (text and images) available on the Internet. The tools are trained on massive data sets that are scraped from Internet sites. And now, these generative AI tools are creating massive amounts of new data that are being fed into the Internet. Therefore, future versions of generative AI tools will be trained with Internet data that is a mix of original and AI-generated data. As time goes on, a mixture of original data and data generated by different versions of AI tools will populate the Internet. This raises a few intriguing questions: how will future versions of generative AI tools behave when trained on a mixture of real and AI generated data? Will they evolve with the new data sets or degenerate? Will evolution introduce biases in subsequent generations of generative AI tools? In this document, we explore these questions and report some very initial simulation results using a simple image-generation AI tool. These results suggest that the quality of the generated images degrades as more AI-generated data is used for training thus suggesting that generative AI may degenerate. Although these results are preliminary and cannot be generalised without further study, they serve to illustrate the potential issues of the interaction between generative AI and the Internet.

Differentially Private Shapley Values for Data Evaluation

The Shapley value has been proposed as a solution to many applications in machine learning, including for equitable valuation of data. Shapley values are computationally expensive and involve the entire dataset. The query for a point's Shapley value can also compromise the statistical privacy of other data points. We observe that in machine learning problems such as empirical risk minimization, and in many learning algorithms (such as those with uniform stability), a diminishing returns property holds, where marginal benefit per data point decreases rapidly with data sample size. Based on this property, we propose a new stratified approximation method called the Layered Shapley Algorithm. We prove that this method operates on small (O(\polylog(n))) random samples of data and small sized ($O(\log n)$) coalitions to achieve the results with guaranteed probabilistic accuracy, and can be modified to incorporate differential privacy. Experimental results show that the algorithm correctly identifies high-value data points that improve validation accuracy, and that the differentially private evaluations preserve approximate ranking of data.

Continual and Sliding Window Release for Private Empirical Risk Minimization

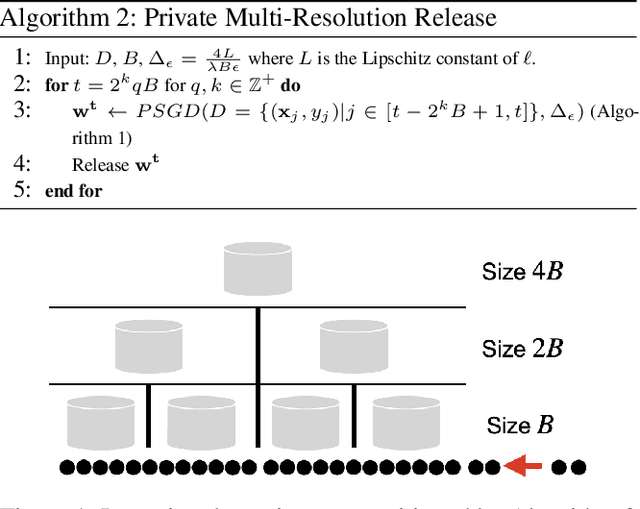
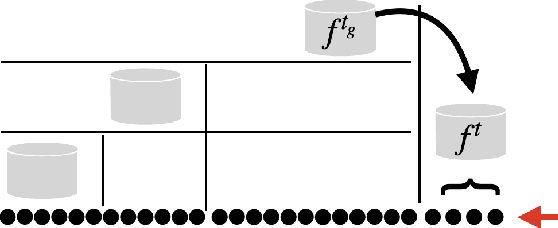
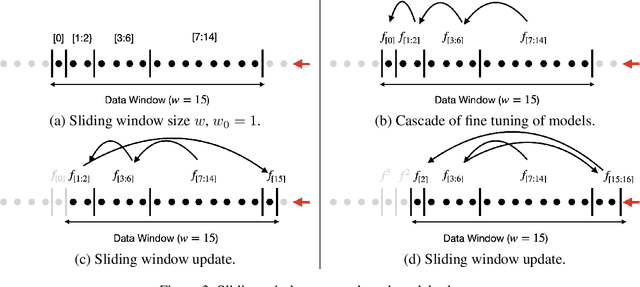
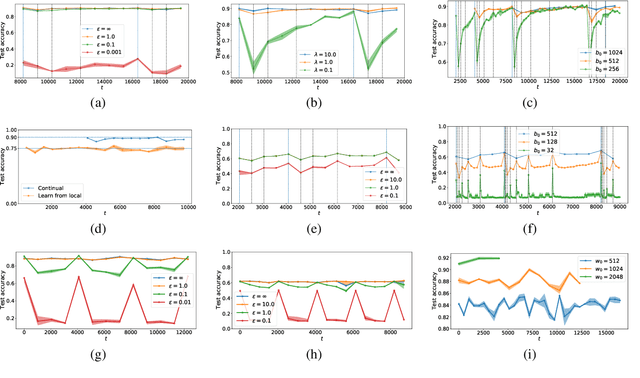
It is difficult to continually update private machine learning models with new data while maintaining privacy. Data incur increasing privacy loss -- as measured by differential privacy -- when they are used in repeated computations. In this paper, we describe regularized empirical risk minimization algorithms that continually release models for a recent window of data. One version of the algorithm uses the entire data history to improve the model for the recent window. The second version uses a sliding window of constant size to improve the model, ensuring more relevant models in case of evolving data. The algorithms operate in the framework of stochastic gradient descent. We prove that even with releasing a model at each time-step over an infinite time horizon, the privacy cost of any data point is bounded by a constant $\epsilon$ differential privacy, and the accuracy of the output models are close to optimal. Experiments on MNIST and Arxiv publications data show results consistent with the theory.

The Shapley Value in Machine Learning

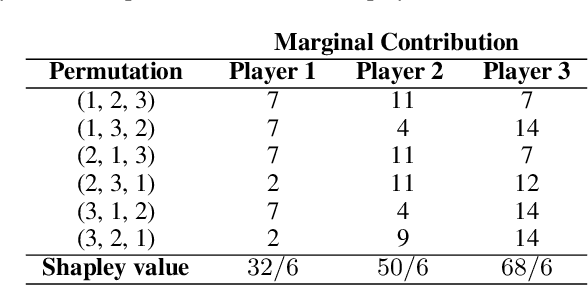
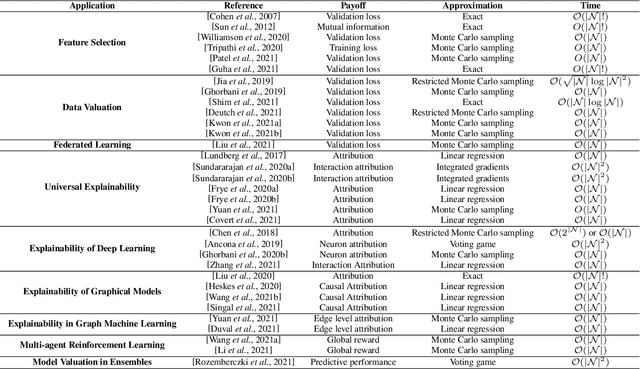
Over the last few years, the Shapley value, a solution concept from cooperative game theory, has found numerous applications in machine learning. In this paper, we first discuss fundamental concepts of cooperative game theory and axiomatic properties of the Shapley value. Then we give an overview of the most important applications of the Shapley value in machine learning: feature selection, explainability, multi-agent reinforcement learning, ensemble pruning, and data valuation. We examine the most crucial limitations of the Shapley value and point out directions for future research.

On the Importance of Difficulty Calibration in Membership Inference Attacks

The vulnerability of machine learning models to membership inference attacks has received much attention in recent years. However, existing attacks mostly remain impractical due to having high false positive rates, where non-member samples are often erroneously predicted as members. This type of error makes the predicted membership signal unreliable, especially since most samples are non-members in real world applications. In this work, we argue that membership inference attacks can benefit drastically from \emph{difficulty calibration}, where an attack's predicted membership score is adjusted to the difficulty of correctly classifying the target sample. We show that difficulty calibration can significantly reduce the false positive rate of a variety of existing attacks without a loss in accuracy.

Stability Enhanced Privacy and Applications in Private Stochastic Gradient Descent

Private machine learning involves addition of noise while training, resulting in lower accuracy. Intuitively, greater stability can imply greater privacy and improve this privacy-utility tradeoff. We study this role of stability in private empirical risk minimization, where differential privacy is achieved by output perturbation, and establish a corresponding theoretical result showing that for strongly-convex loss functions, an algorithm with uniform stability of $\beta$ implies a bound of $O(\sqrt{\beta})$ on the scale of noise required for differential privacy. The result applies to both explicit regularization and to implicitly stabilized ERM, such as adaptations of Stochastic Gradient Descent that are known to be stable. Thus, it generalizes recent results that improve privacy through modifications to SGD, and establishes stability as the unifying perspective. It implies new privacy guarantees for optimizations with uniform stability guarantees, where a corresponding differential privacy guarantee was previously not known. Experimental results validate the utility of stability enhanced privacy in several problems, including application of elastic nets and feature selection.