Continual and Sliding Window Release for Private Empirical Risk Minimization
Paper and Code
Mar 07, 2022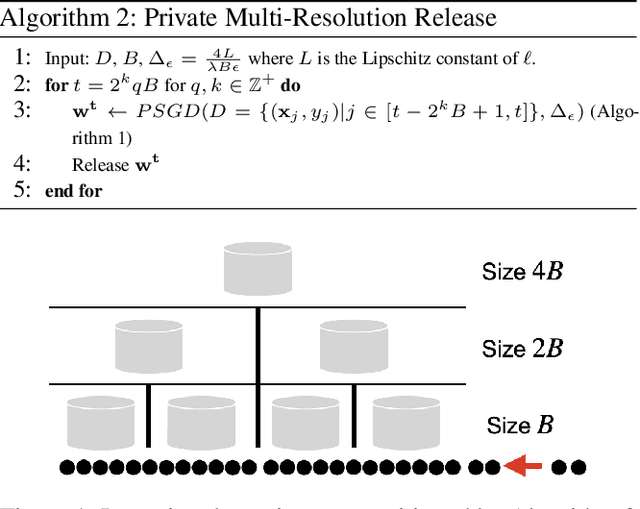
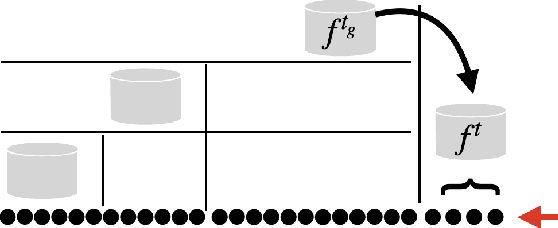
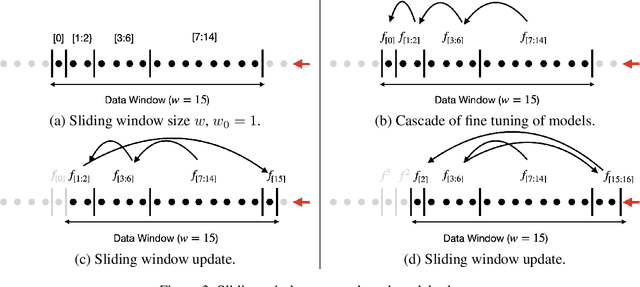
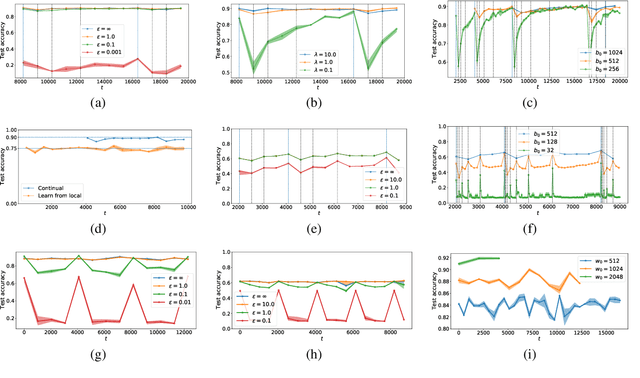
It is difficult to continually update private machine learning models with new data while maintaining privacy. Data incur increasing privacy loss -- as measured by differential privacy -- when they are used in repeated computations. In this paper, we describe regularized empirical risk minimization algorithms that continually release models for a recent window of data. One version of the algorithm uses the entire data history to improve the model for the recent window. The second version uses a sliding window of constant size to improve the model, ensuring more relevant models in case of evolving data. The algorithms operate in the framework of stochastic gradient descent. We prove that even with releasing a model at each time-step over an infinite time horizon, the privacy cost of any data point is bounded by a constant $\epsilon$ differential privacy, and the accuracy of the output models are close to optimal. Experiments on MNIST and Arxiv publications data show results consistent with the theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge