Approximating Metric Magnitude of Point Sets
Paper and Code
Sep 06, 2024


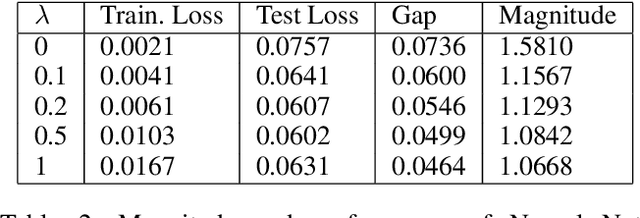
Metric magnitude is a measure of the "size" of point clouds with many desirable geometric properties. It has been adapted to various mathematical contexts and recent work suggests that it can enhance machine learning and optimization algorithms. But its usability is limited due to the computational cost when the dataset is large or when the computation must be carried out repeatedly (e.g. in model training). In this paper, we study the magnitude computation problem, and show efficient ways of approximating it. We show that it can be cast as a convex optimization problem, but not as a submodular optimization. The paper describes two new algorithms - an iterative approximation algorithm that converges fast and is accurate, and a subset selection method that makes the computation even faster. It has been previously proposed that magnitude of model sequences generated during stochastic gradient descent is correlated to generalization gap. Extension of this result using our more scalable algorithms shows that longer sequences in fact bear higher correlations. We also describe new applications of magnitude in machine learning - as an effective regularizer for neural network training, and as a novel clustering criterion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge