Approximating Metric Magnitude of Point Sets

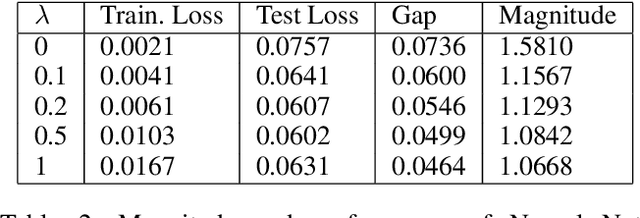
Metric magnitude is a measure of the "size" of point clouds with many desirable geometric properties. It has been adapted to various mathematical contexts and recent work suggests that it can enhance machine learning and optimization algorithms. But its usability is limited due to the computational cost when the dataset is large or when the computation must be carried out repeatedly (e.g. in model training). In this paper, we study the magnitude computation problem, and show efficient ways of approximating it. We show that it can be cast as a convex optimization problem, but not as a submodular optimization. The paper describes two new algorithms - an iterative approximation algorithm that converges fast and is accurate, and a subset selection method that makes the computation even faster. It has been previously proposed that magnitude of model sequences generated during stochastic gradient descent is correlated to generalization gap. Extension of this result using our more scalable algorithms shows that longer sequences in fact bear higher correlations. We also describe new applications of magnitude in machine learning - as an effective regularizer for neural network training, and as a novel clustering criterion.

A Topology Layer for Machine Learning

Topology applied to real world data using persistent homology has started to find applications within machine learning, including deep learning. We present a differentiable topology layer that computes persistent homology based on level set filtrations and distance-bases filtrations. We present three novel applications: the topological layer can (i) serve as a regularizer directly on data or the weights of machine learning models, (ii) construct a loss on the output of a deep generative network to incorporate topological priors, and (iii) perform topological adversarial attacks on deep networks trained with persistence features. The code is publicly available and we hope its availability will facilitate the use of persistent homology in deep learning and other gradient based applications.

News Across Languages - Cross-Lingual Document Similarity and Event Tracking

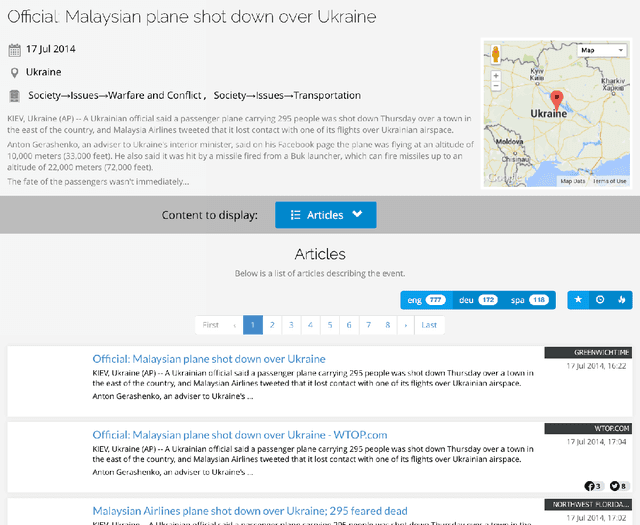
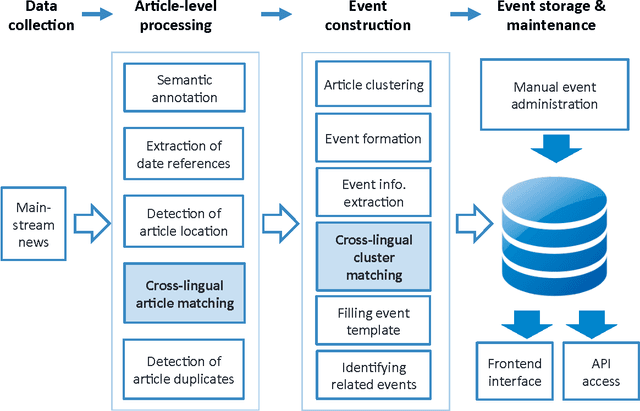
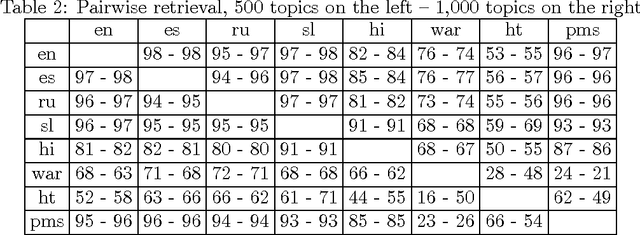
In today's world, we follow news which is distributed globally. Significant events are reported by different sources and in different languages. In this work, we address the problem of tracking of events in a large multilingual stream. Within a recently developed system Event Registry we examine two aspects of this problem: how to compare articles in different languages and how to link collections of articles in different languages which refer to the same event. Taking a multilingual stream and clusters of articles from each language, we compare different cross-lingual document similarity measures based on Wikipedia. This allows us to compute the similarity of any two articles regardless of language. Building on previous work, we show there are methods which scale well and can compute a meaningful similarity between articles from languages with little or no direct overlap in the training data. Using this capability, we then propose an approach to link clusters of articles across languages which represent the same event. We provide an extensive evaluation of the system as a whole, as well as an evaluation of the quality and robustness of the similarity measure and the linking algorithm.

A Comparison of Relaxations of Multiset Cannonical Correlation Analysis and Applications

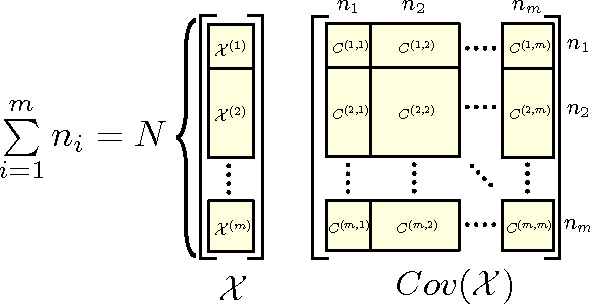
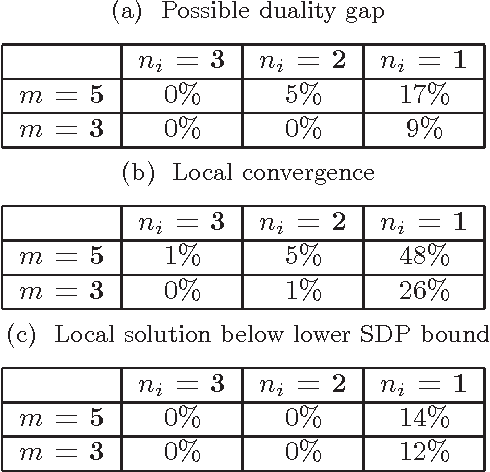
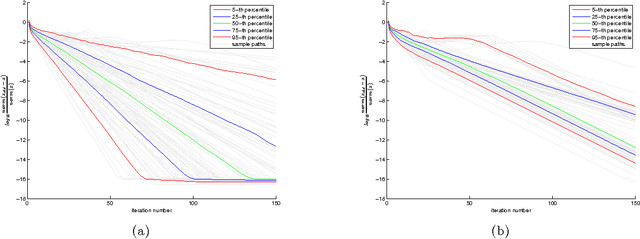
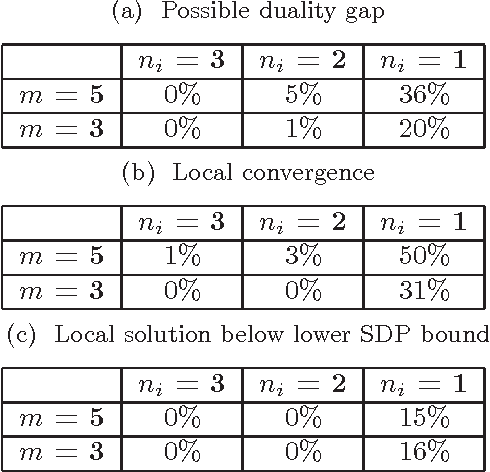
Canonical correlation analysis is a statistical technique that is used to find relations between two sets of variables. An important extension in pattern analysis is to consider more than two sets of variables. This problem can be expressed as a quadratically constrained quadratic program (QCQP), commonly referred to Multi-set Canonical Correlation Analysis (MCCA). This is a non-convex problem and so greedy algorithms converge to local optima without any guarantees on global optimality. In this paper, we show that despite being highly structured, finding the optimal solution is NP-Hard. This motivates our relaxation of the QCQP to a semidefinite program (SDP). The SDP is convex, can be solved reasonably efficiently and comes with both absolute and output-sensitive approximation quality. In addition to theoretical guarantees, we do an extensive comparison of the QCQP method and the SDP relaxation on a variety of synthetic and real world data. Finally, we present two useful extensions: we incorporate kernel methods and computing multiple sets of canonical vectors.