What is an equivariant neural network?

We explain equivariant neural networks, a notion underlying breakthroughs in machine learning from deep convolutional neural networks for computer vision to AlphaFold 2 for protein structure prediction, without assuming knowledge of equivariance or neural networks. The basic mathematical ideas are simple but are often obscured by engineering complications that come with practical realizations. We extract and focus on the mathematical aspects, and limit ourselves to a cursory treatment of the engineering issues at the end.

Topology-Preserving Dimensionality Reduction via Interleaving Optimization

Dimensionality reduction techniques are powerful tools for data preprocessing and visualization which typically come with few guarantees concerning the topological correctness of an embedding. The interleaving distance between the persistent homology of Vietoris-Rips filtrations can be used to identify a scale at which topological features such as clusters or holes in an embedding and original data set are in correspondence. We show how optimization seeking to minimize the interleaving distance can be incorporated into dimensionality reduction algorithms, and explicitly demonstrate its use in finding an optimal linear projection. We demonstrate the utility of this framework to data visualization.

Topological Regularization for Dense Prediction

Dense prediction tasks such as depth perception and semantic segmentation are important applications in computer vision that have a concrete topological description in terms of partitioning an image into connected components or estimating a function with a small number of local extrema corresponding to objects in the image. We develop a form of topological regularization based on persistent homology that can be used in dense prediction tasks with these topological descriptions. Experimental results show that the output topology can also appear in the internal activations of trained neural networks which allows for a novel use of topological regularization to the internal states of neural networks during training, reducing the computational cost of the regularization. We demonstrate that this topological regularization of internal activations leads to improved convergence and test benchmarks on several problems and architectures.

Clustering of Electromagnetic Showers and Particle Interactions with Graph Neural Networks in Liquid Argon Time Projection Chambers Data

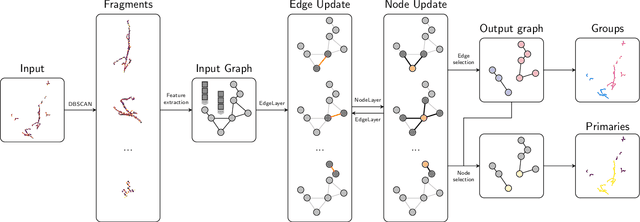
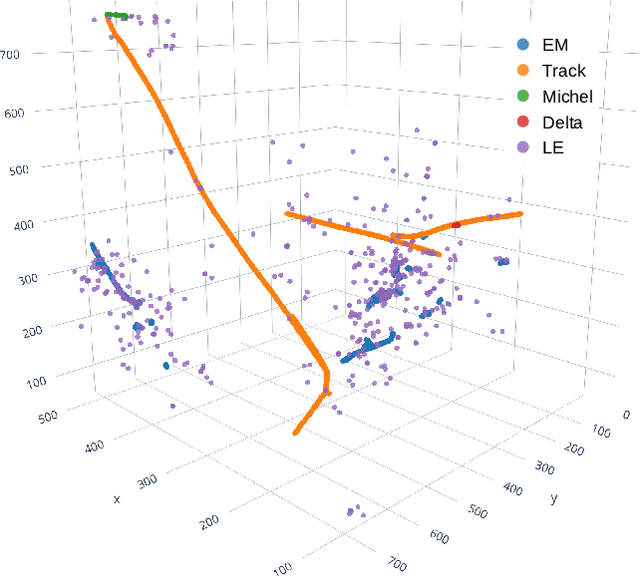
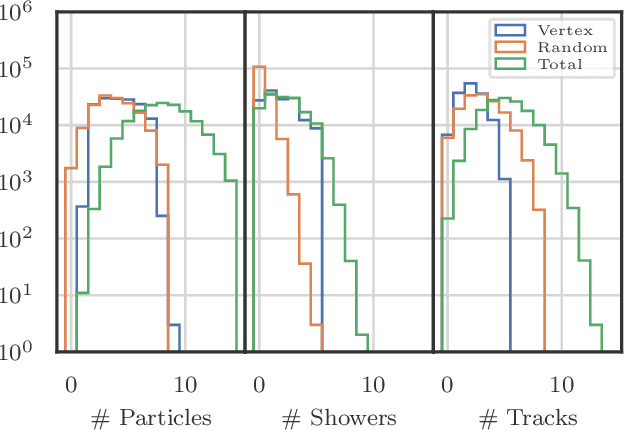
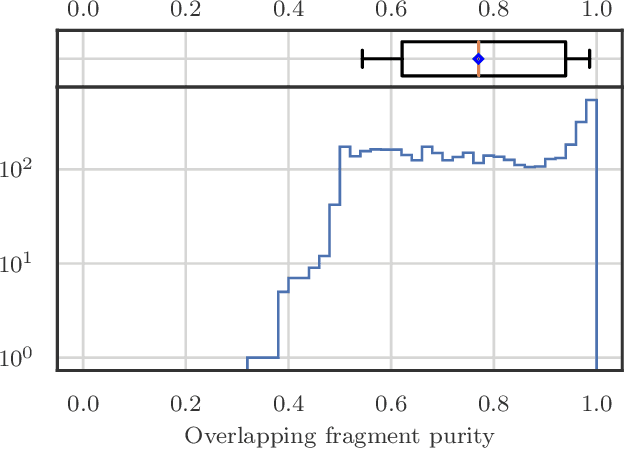
Liquid Argon Time Projection Chambers (LArTPCs) are a class of detectors that produce high resolution images of charged particles within their sensitive volume. In these images, the clustering of distinct particles into superstructures is of central importance to the current and future neutrino physics program. Electromagnetic (EM) activity typically exhibits spatially detached fragments of varying morphology and orientation that are challenging to efficiently assemble using traditional algorithms. Similarly, particles that are spatially removed from each other in the detector may originate from a common interaction. Graph Neural Networks (GNNs) were developed in recent years to find correlations between objects embedded in an arbitrary space. GNNs are first studied with the goal of predicting the adjacency matrix of EM shower fragments and to identify the origin of showers, i.e. primary fragments. On the PILArNet public LArTPC simulation dataset, the algorithm developed in this paper achieves a shower clustering accuracy characterized by a mean adjusted Rand index (ARI) of 97.8 % and a primary identification accuracy of 99.8 %. It yields a relative shower energy resolution of $(4.1+1.4/\sqrt{E (\text{GeV})})\,\%$ and a shower direction resolution of $(2.1/\sqrt{E(\text{GeV})})^{\circ}$. The optimized GNN is then applied to the related task of clustering particle instances into interactions and yields a mean ARI of 99.2 % for an interaction density of $\sim\mathcal{O}(1)\,m^{-3}$.

Modeling Electromagnetic Navigation Systems for Medical Applications using Random Forests and Artificial Neural Networks

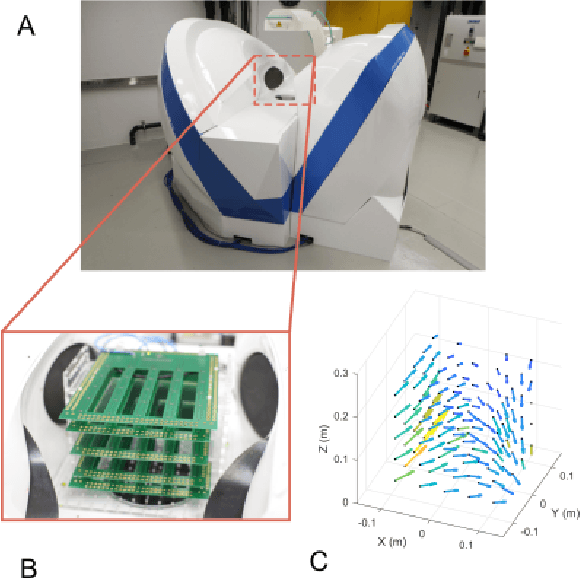
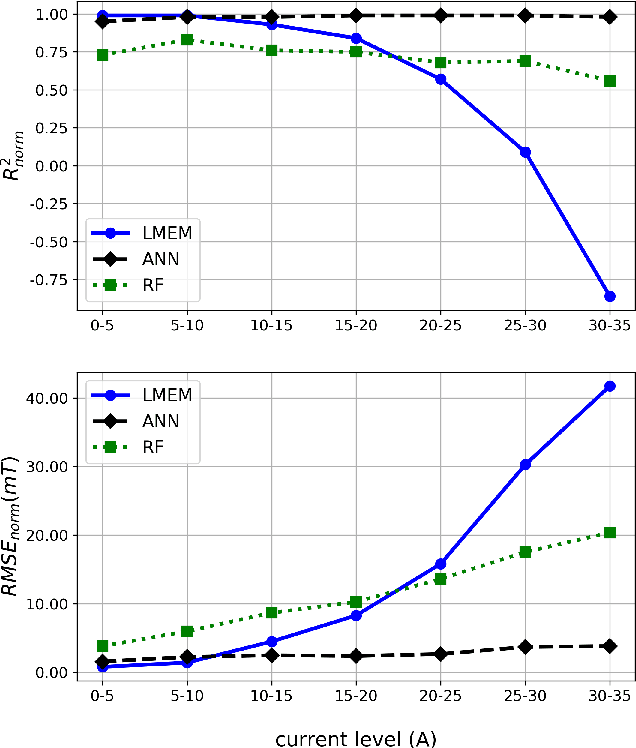
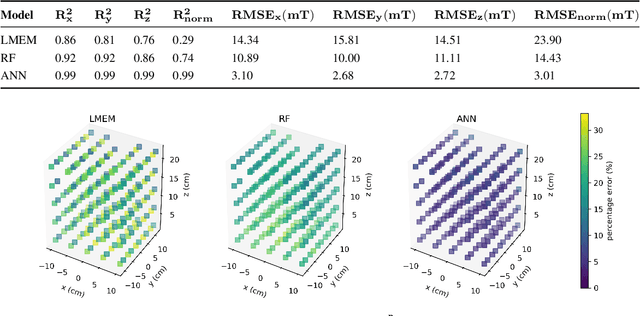
Electromagnetic Navigation Systems (eMNS) can be used to control a variety of multiscale devices within the human body for remote surgery. Accurate modeling of the magnetic fields generated by the electromagnets of an eMNS is crucial for the precise control of these devices. Existing methods assume a linear behavior of these systems, leading to significant modeling errors within nonlinear regions exhibited at higher magnetic fields. In this paper, we use a random forest (RF) and an artificial neural network (ANN) to model the nonlinear behavior of the magnetic fields generated by an eMNS. Both machine learning methods outperformed the state-of-the-art linear multipole electromagnet method (LMEM). The RF and the ANN model reduced the root mean squared error of the LMEM when predicting the field magnitude by around 40% and 80%, respectively, over the entire current range of the eMNS. At high current regions, especially between 30 and 35 A, the field-magnitude RMSE improvement of the ANN model over the LMEM was over 35 mT. This study demonstrates the feasibility of using machine learning methods to model an eMNS for medical applications, and its ability to account for complex nonlinear behavior at high currents. The use of machine learning thus shows promise for improving surgical procedures that use magnetic navigation.

A Topology Layer for Machine Learning

Topology applied to real world data using persistent homology has started to find applications within machine learning, including deep learning. We present a differentiable topology layer that computes persistent homology based on level set filtrations and distance-bases filtrations. We present three novel applications: the topological layer can (i) serve as a regularizer directly on data or the weights of machine learning models, (ii) construct a loss on the output of a deep generative network to incorporate topological priors, and (iii) perform topological adversarial attacks on deep networks trained with persistence features. The code is publicly available and we hope its availability will facilitate the use of persistent homology in deep learning and other gradient based applications.