Rényi Differential Privacy for Heavy-Tailed SDEs via Fractional Poincaré Inequalities

Characterizing the differential privacy (DP) of learning algorithms has become a major challenge in recent years. In parallel, many studies suggested investigating the behavior of stochastic gradient descent (SGD) with heavy-tailed noise, both as a model for modern deep learning models and to improve their performance. However, most DP bounds focus on light-tailed noise, where satisfactory guarantees have been obtained but the proposed techniques do not directly extend to the heavy-tailed setting. Recently, the first DP guarantees for heavy-tailed SGD were obtained. These results provide $(0,δ)$-DP guarantees without requiring gradient clipping. Despite casting new light on the link between DP and heavy-tailed algorithms, these results have a strong dependence on the number of parameters and cannot be extended to other DP notions like the well-established Rényi differential privacy (RDP). In this work, we propose to address these limitations by deriving the first RDP guarantees for heavy-tailed SDEs, as well as their discretized counterparts. Our framework is based on new Rényi flow computations and the use of well-established fractional Poincaré inequalities. Under the assumption that such inequalities are satisfied, we obtain DP guarantees that have a much weaker dependence on the dimension compared to prior art.

Mutual Information Free Topological Generalization Bounds via Stability

Providing generalization guarantees for stochastic optimization algorithms is a major challenge in modern learning theory. Recently, several studies highlighted the impact of the geometry of training trajectories on the generalization error, both theoretically and empirically. Among these works, a series of topological generalization bounds have been proposed, relating the generalization error to notions of topological complexity that stem from topological data analysis (TDA). Despite their empirical success, these bounds rely on intricate information-theoretic (IT) terms that can be bounded in specific cases but remain intractable for practical algorithms (such as ADAM), potentially reducing the relevance of the derived bounds. In this paper, we seek to formulate comprehensive and interpretable topological generalization bounds free of intractable mutual information terms. To this end, we introduce a novel learning theoretic framework that departs from the existing strategies via proof techniques rooted in algorithmic stability. By extending an existing notion of \textit{hypothesis set stability}, to \textit{trajectory stability}, we prove that the generalization error of trajectory-stable algorithms can be upper bounded in terms of (i) TDA quantities describing the complexity of the trajectory of the optimizer in the parameter space, and (ii) the trajectory stability parameter of the algorithm. Through a series of experimental evaluations, we demonstrate that the TDA terms in the bound are of great importance, especially as the number of training samples grows. This ultimately forms an explanation of the empirical success of the topological generalization bounds.

Algorithm- and Data-Dependent Generalization Bounds for Score-Based Generative Models

Score-based generative models (SGMs) have emerged as one of the most popular classes of generative models. A substantial body of work now exists on the analysis of SGMs, focusing either on discretization aspects or on their statistical performance. In the latter case, bounds have been derived, under various metrics, between the true data distribution and the distribution induced by the SGM, often demonstrating polynomial convergence rates with respect to the number of training samples. However, these approaches adopt a largely approximation theory viewpoint, which tends to be overly pessimistic and relatively coarse. In particular, they fail to fully explain the empirical success of SGMs or capture the role of the optimization algorithm used in practice to train the score network. To support this observation, we first present simple experiments illustrating the concrete impact of optimization hyperparameters on the generalization ability of the generated distribution. Then, this paper aims to bridge this theoretical gap by providing the first algorithmic- and data-dependent generalization analysis for SGMs. In particular, we establish bounds that explicitly account for the optimization dynamics of the learning algorithm, offering new insights into the generalization behavior of SGMs. Our theoretical findings are supported by empirical results on several datasets.

Understanding the Generalization Error of Markov algorithms through Poissonization

Using continuous-time stochastic differential equation (SDE) proxies to stochastic optimization algorithms has proven fruitful for understanding their generalization abilities. A significant part of these approaches are based on the so-called ``entropy flows'', which greatly simplify the generalization analysis. Unfortunately, such well-structured entropy flows cannot be obtained for most discrete-time algorithms, and the existing SDE approaches remain limited to specific noise and algorithmic structures. We aim to alleviate this issue by introducing a generic framework for analyzing the generalization error of Markov algorithms through `Poissonization', a continuous-time approximation of discrete-time processes with formal approximation guarantees. Through this approach, we first develop a novel entropy flow, which directly leads to PAC-Bayesian generalization bounds. We then draw novel links to modified versions of the celebrated logarithmic Sobolev inequalities (LSI), identify cases where such LSIs are satisfied, and obtain improved bounds. Beyond its generality, our framework allows exploiting specific properties of learning algorithms. In particular, we incorporate the noise structure of different algorithm types - namely, those with additional noise injections (noisy) and those without (non-noisy) - through various technical tools. This illustrates the capacity of our methods to achieve known (yet, Poissonized) and new generalization bounds.

Topological Generalization Bounds for Discrete-Time Stochastic Optimization Algorithms

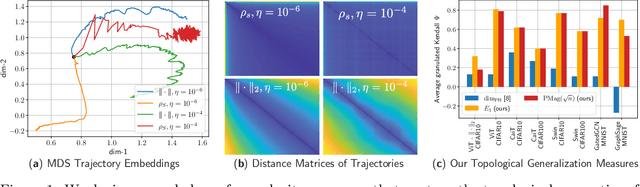
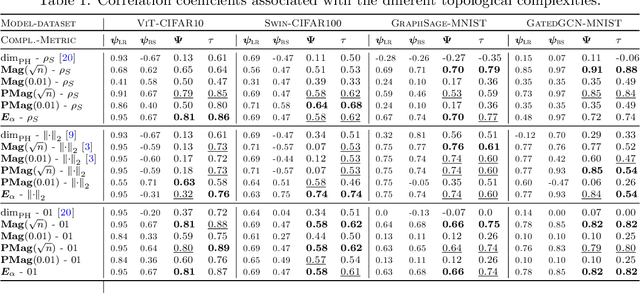
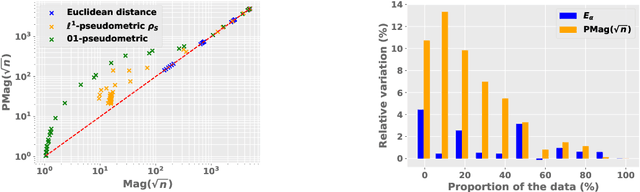
We present a novel set of rigorous and computationally efficient topology-based complexity notions that exhibit a strong correlation with the generalization gap in modern deep neural networks (DNNs). DNNs show remarkable generalization properties, yet the source of these capabilities remains elusive, defying the established statistical learning theory. Recent studies have revealed that properties of training trajectories can be indicative of generalization. Building on this insight, state-of-the-art methods have leveraged the topology of these trajectories, particularly their fractal dimension, to quantify generalization. Most existing works compute this quantity by assuming continuous- or infinite-time training dynamics, complicating the development of practical estimators capable of accurately predicting generalization without access to test data. In this paper, we respect the discrete-time nature of training trajectories and investigate the underlying topological quantities that can be amenable to topological data analysis tools. This leads to a new family of reliable topological complexity measures that provably bound the generalization error, eliminating the need for restrictive geometric assumptions. These measures are computationally friendly, enabling us to propose simple yet effective algorithms for computing generalization indices. Moreover, our flexible framework can be extended to different domains, tasks, and architectures. Our experimental results demonstrate that our new complexity measures correlate highly with generalization error in industry-standards architectures such as transformers and deep graph networks. Our approach consistently outperforms existing topological bounds across a wide range of datasets, models, and optimizers, highlighting the practical relevance and effectiveness of our complexity measures.

Uniform Generalization Bounds on Data-Dependent Hypothesis Sets via PAC-Bayesian Theory on Random Sets

We propose data-dependent uniform generalization bounds by approaching the problem from a PAC-Bayesian perspective. We first apply the PAC-Bayesian framework on `random sets' in a rigorous way, where the training algorithm is assumed to output a data-dependent hypothesis set after observing the training data. This approach allows us to prove data-dependent bounds, which can be applicable in numerous contexts. To highlight the power of our approach, we consider two main applications. First, we propose a PAC-Bayesian formulation of the recently developed fractal-dimension-based generalization bounds. The derived results are shown to be tighter and they unify the existing results around one simple proof technique. Second, we prove uniform bounds over the trajectories of continuous Langevin dynamics and stochastic gradient Langevin dynamics. These results provide novel information about the generalization properties of noisy algorithms.

Generalization Bounds for Heavy-Tailed SDEs through the Fractional Fokker-Planck Equation

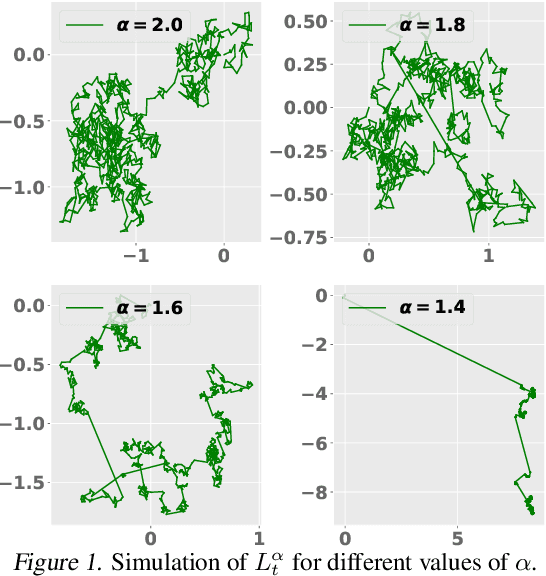
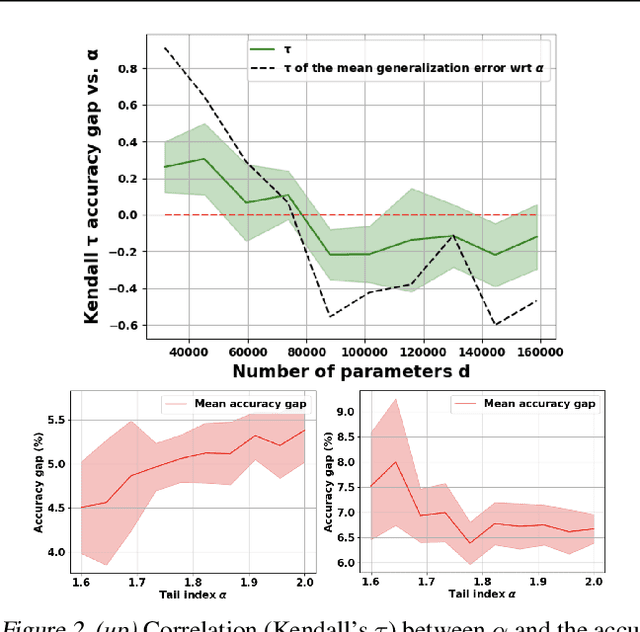
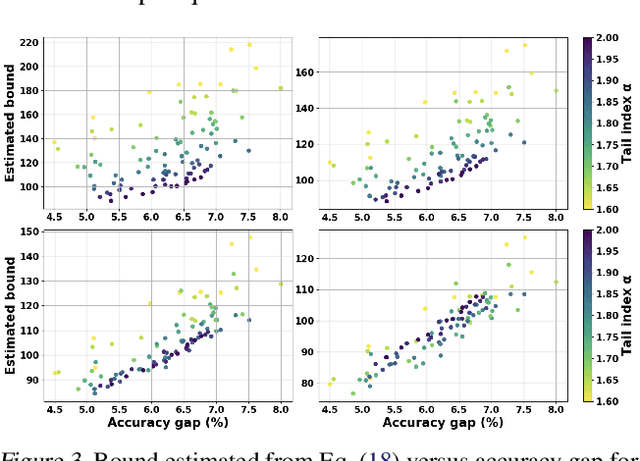
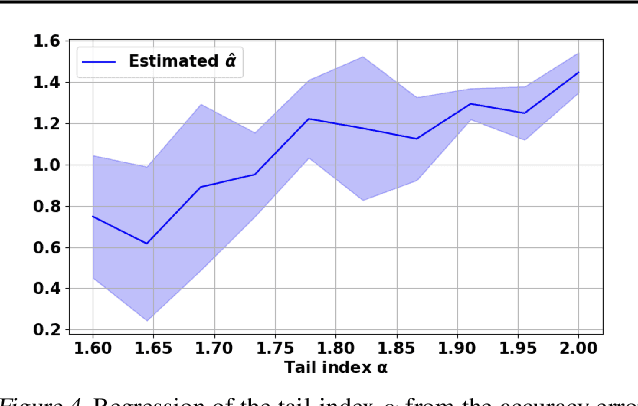
Understanding the generalization properties of heavy-tailed stochastic optimization algorithms has attracted increasing attention over the past years. While illuminating interesting aspects of stochastic optimizers by using heavy-tailed stochastic differential equations as proxies, prior works either provided expected generalization bounds, or introduced non-computable information theoretic terms. Addressing these drawbacks, in this work, we prove high-probability generalization bounds for heavy-tailed SDEs which do not contain any nontrivial information theoretic terms. To achieve this goal, we develop new proof techniques based on estimating the entropy flows associated with the so-called fractional Fokker-Planck equation (a partial differential equation that governs the evolution of the distribution of the corresponding heavy-tailed SDE). In addition to obtaining high-probability bounds, we show that our bounds have a better dependence on the dimension of parameters as compared to prior art. Our results further identify a phase transition phenomenon, which suggests that heavy tails can be either beneficial or harmful depending on the problem structure. We support our theory with experiments conducted in a variety of settings.

From Mutual Information to Expected Dynamics: New Generalization Bounds for Heavy-Tailed SGD

Understanding the generalization abilities of modern machine learning algorithms has been a major research topic over the past decades. In recent years, the learning dynamics of Stochastic Gradient Descent (SGD) have been related to heavy-tailed dynamics. This has been successfully applied to generalization theory by exploiting the fractal properties of those dynamics. However, the derived bounds depend on mutual information (decoupling) terms that are beyond the reach of computability. In this work, we prove generalization bounds over the trajectory of a class of heavy-tailed dynamics, without those mutual information terms. Instead, we introduce a geometric decoupling term by comparing the learning dynamics (depending on the empirical risk) with an expected one (depending on the population risk). We further upper-bound this geometric term, by using techniques from the heavy-tailed and the fractal literature, making it fully computable. Moreover, as an attempt to tighten the bounds, we propose a PAC-Bayesian setting based on perturbed dynamics, in which the same geometric term plays a crucial role and can still be bounded using the techniques described above.

Generalization Bounds with Data-dependent Fractal Dimensions

Providing generalization guarantees for modern neural networks has been a crucial task in statistical learning. Recently, several studies have attempted to analyze the generalization error in such settings by using tools from fractal geometry. While these works have successfully introduced new mathematical tools to apprehend generalization, they heavily rely on a Lipschitz continuity assumption, which in general does not hold for neural networks and might make the bounds vacuous. In this work, we address this issue and prove fractal geometry-based generalization bounds without requiring any Lipschitz assumption. To achieve this goal, we build up on a classical covering argument in learning theory and introduce a data-dependent fractal dimension. Despite introducing a significant amount of technical complications, this new notion lets us control the generalization error (over either fixed or random hypothesis spaces) along with certain mutual information (MI) terms. To provide a clearer interpretation to the newly introduced MI terms, as a next step, we introduce a notion of "geometric stability" and link our bounds to the prior art. Finally, we make a rigorous connection between the proposed data-dependent dimension and topological data analysis tools, which then enables us to compute the dimension in a numerically efficient way. We support our theory with experiments conducted on various settings.

DNN-Based Topology Optimisation: Spatial Invariance and Neural Tangent Kernel

We study the SIMP method with a density field generated by a fully-connected neural network, taking the coordinates as inputs. In the large width limit, we show that the use of DNNs leads to a filtering effect similar to traditional filtering techniques for SIMP, with a filter described by the Neural Tangent Kernel (NTK). This filter is however not invariant under translation, leading to visual artifacts and non-optimal shapes. We propose two embeddings of the input coordinates, which lead to (approximate) spatial invariance of the NTK and of the filter. We empirically confirm our theoretical observations and study how the filter size is affected by the architecture of the network. Our solution can easily be applied to any other coordinates-based generation method.